sklearn中调用PCA算法
sklearn中调用PCA算法
PCA算法是一种数据降维的方法,它可以对于数据进行维度降低,实现提高数据计算和训练的效率,而不丢失数据的重要信息,其sklearn中调用PCA算法的具体操作和代码如下所示:
#sklearn中调用PCA函数进行相关的训练和计算(自定义数据)
import numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.0,100.0,size=100)
x[:,1]=0.75*x[:,0]+3.0*np.random.normal(0,3,size=100)
plt.figure()
plt.scatter(x[:,0],x[:,1])
plt.show()
from sklearn.decomposition import PCA #在sklearn中调用PCA机器学习算法
pca=PCA(n_components=1) #定义所需要分析主成分的个数n
pca.fit(x) #对基础数据集进行相关的计算,求取相应的主成分
print(pca.components_) #输出相应的n个主成分的单位向量方向
x_reduction=pca.transform(x) #进行数据的降维
x_restore=pca.inverse_transform(x_reduction) #对降维数据进行相关的恢复工作
plt.figure()
plt.scatter(x[:,0],x[:,1],color="g")
plt.scatter(x_restore[:,0],x_restore[:,1],color="r")
plt.show()
#sklearn中利用手写字体的数据集进行实际的PCA算法
#1-1导入相应的库函数
from sklearn import datasets
d=datasets.load_digits()
x=d.data
y=d.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
print(x_train.shape)
from sklearn.neighbors import KNeighborsClassifier
knn=KNeighborsClassifier()
knn.fit(x_train,y_train)
print(knn.score(x_test,y_test))
#1-2对于64维的原始数据进行降维,降到2维数据
pca1=PCA(n_components=2)
pca1.fit(x_train)
x_train_re=pca1.transform(x_train) #对于训练数据和测试数据进行降维到二维数据
x_test_re=pca1.transform(x_test)
knn1=KNeighborsClassifier()
knn1.fit(x_train_re,y_train) #再对降维到的二维数据进行KNN算法的训练和测试准确度
print(knn1.score(x_test_re,y_test))
print(pca1.explained_variance_ratio_)
#1-3-1对于训练数据和测试数据进行降维到64维数据,维度不变
pca2=PCA(n_components=64) #对于训练数据和测试数据进行降维到64维数据,维度不变
pca2.fit(x_train)
x_train_re=pca2.transform(x_train)
x_test_re=pca2.transform(x_test)
knn1=KNeighborsClassifier()
knn1.fit(x_train_re,y_train)
print(knn1.score(x_test_re,y_test))
print(pca2.explained_variance_ratio_) #输出各个主成分对于整体数据的方差的体现比例
#1-3-2输出前n个主成分所能够反映的数据的特征权重
plt.figure()
plt.plot([i for i in range(x.shape[1])],[np.sum(pca2.explained_variance_ratio_[:i+1]) for i in range(x.shape[1])])
plt.show()
#1-4PCA(a)括号里面的a为0-1的数字,表示输出满足能够反映原始数据比重为a时的最低维度时的PCA,之后进行训练和分类会提高计算的效率5-10倍,但是分类准确度基本相差无几,可以用准确度来换取计算的效率
pca3=PCA(0.95)
pca3.fit(x_train)
print(pca3.n_components_) #输出此时降到的数据维度
x_train_re1=pca3.transform(x_train)
x_test_re1=pca3.transform(x_test)
knn2=KNeighborsClassifier()
knn2.fit(x_train_re1,y_train)
print(knn2.score(x_test_re1,y_test))
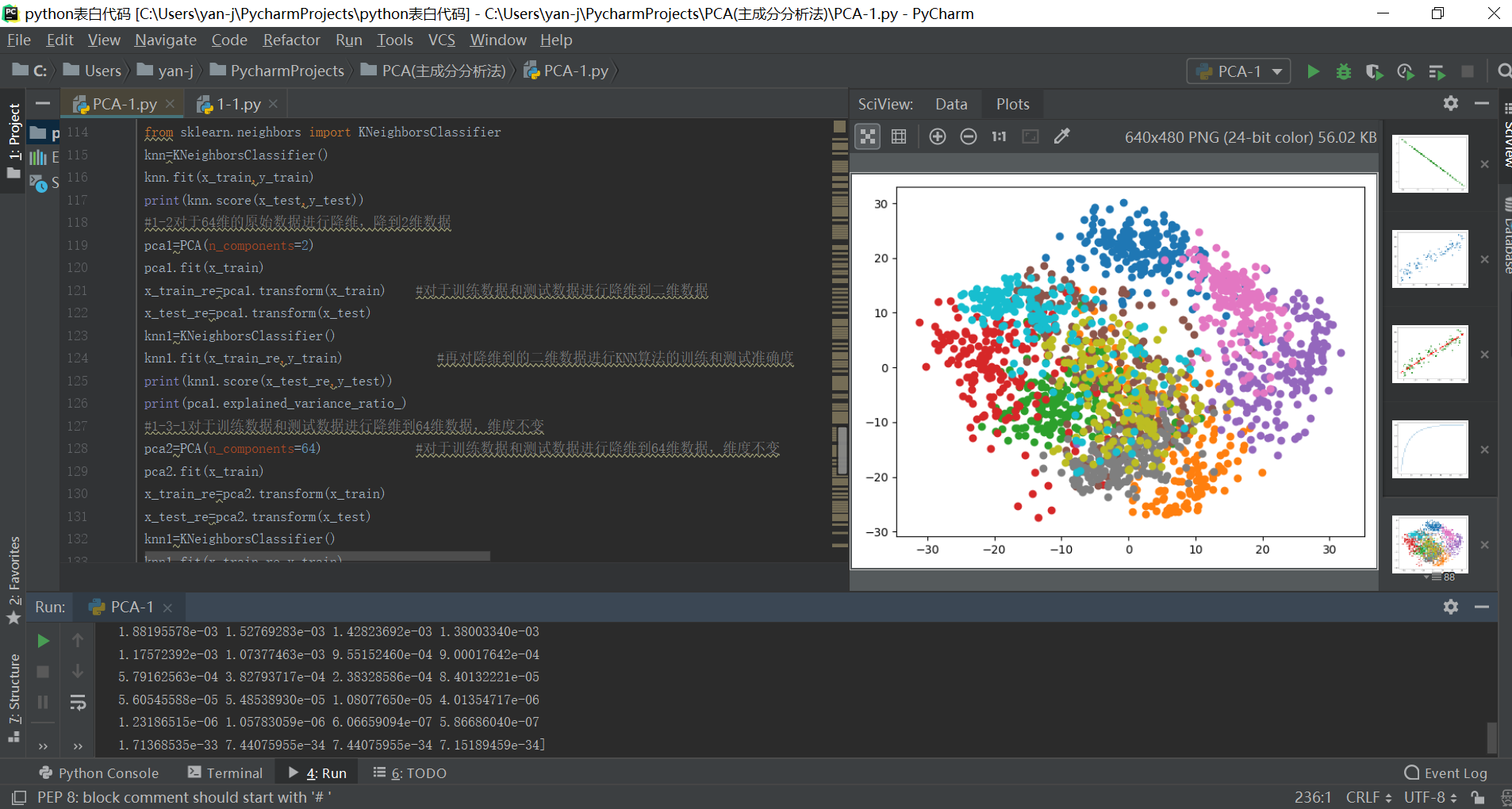
#1-5对于64维度数据进行降维到二维数据,之后进行数据的可视化,可以对于不同的分类结果进行查询和可视化区分
pca1=PCA(n_components=2)
pca1.fit(x)
x_re=pca1.transform(x)
plt.figure()
for i in range(10):
plt.scatter(x_re[y==i,0],x_re[y==i,1])
plt.show()
输出结果如下所示:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号