python实现PCA算法原理

PCA主成分分析法的数据主成分分析过程及python原理实现

1、对于主成分分析法，在求得第一主成分之后，如果需要求取下一个主成分，则需要将原来数据把第一主成分去掉以后再求取新的数据X’的第一主成分，即为原来数据X的第二主成分，循环往复即可。

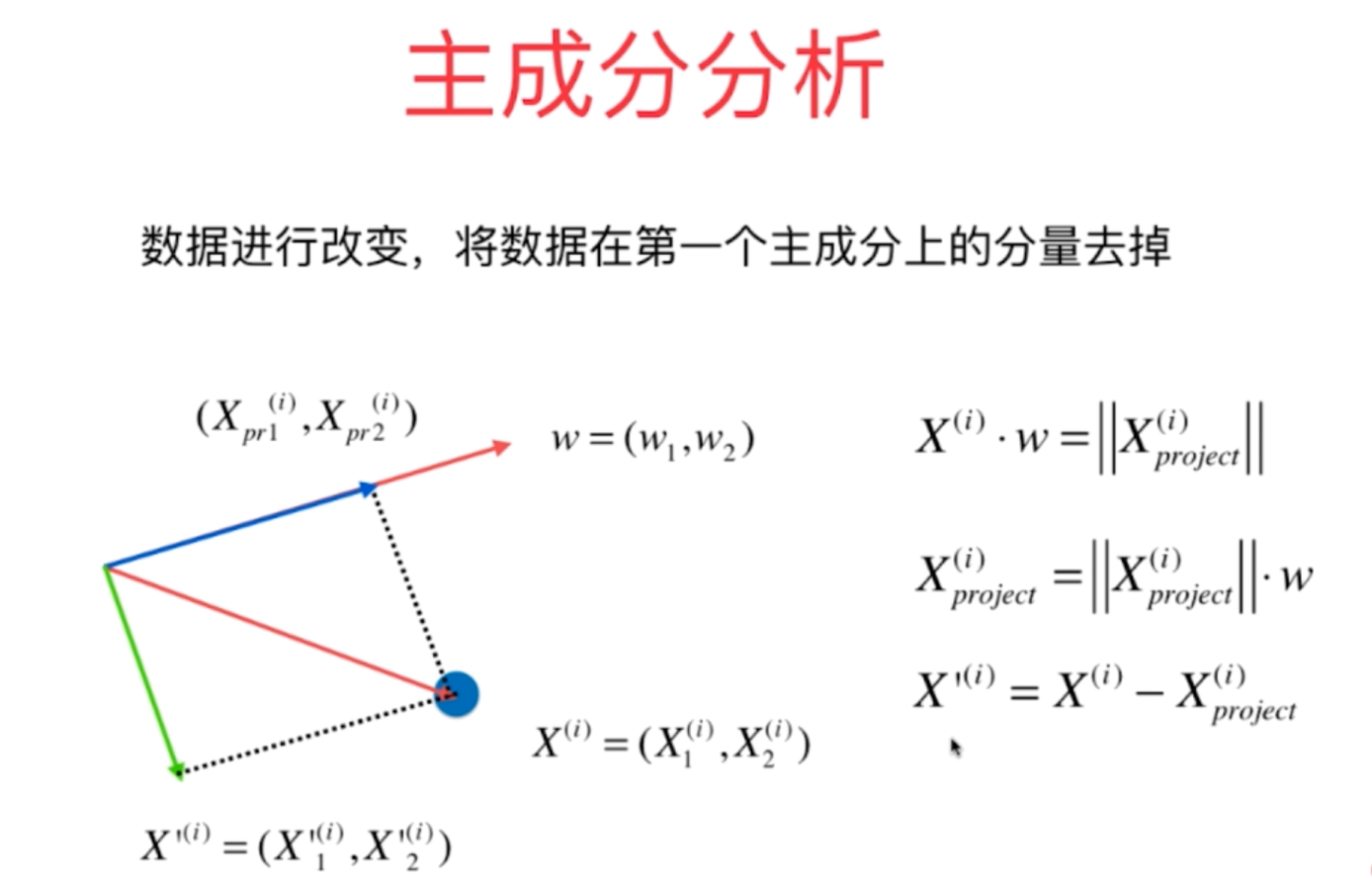
2、利用PCA算法的原理进行数据的降维，其计算过程的数学原理如下所示，其降维的过程会丢失一定的信息，因此采用恢复过程恢复原来的高维数据后，它会恢复为原来数据在新的主成分上的映射点，而不再是原来的坐标点。

（1）高维数据的降维（从n维降到k维数据）

（2）从降维得到k维数据恢复到原来的n维数据集

 

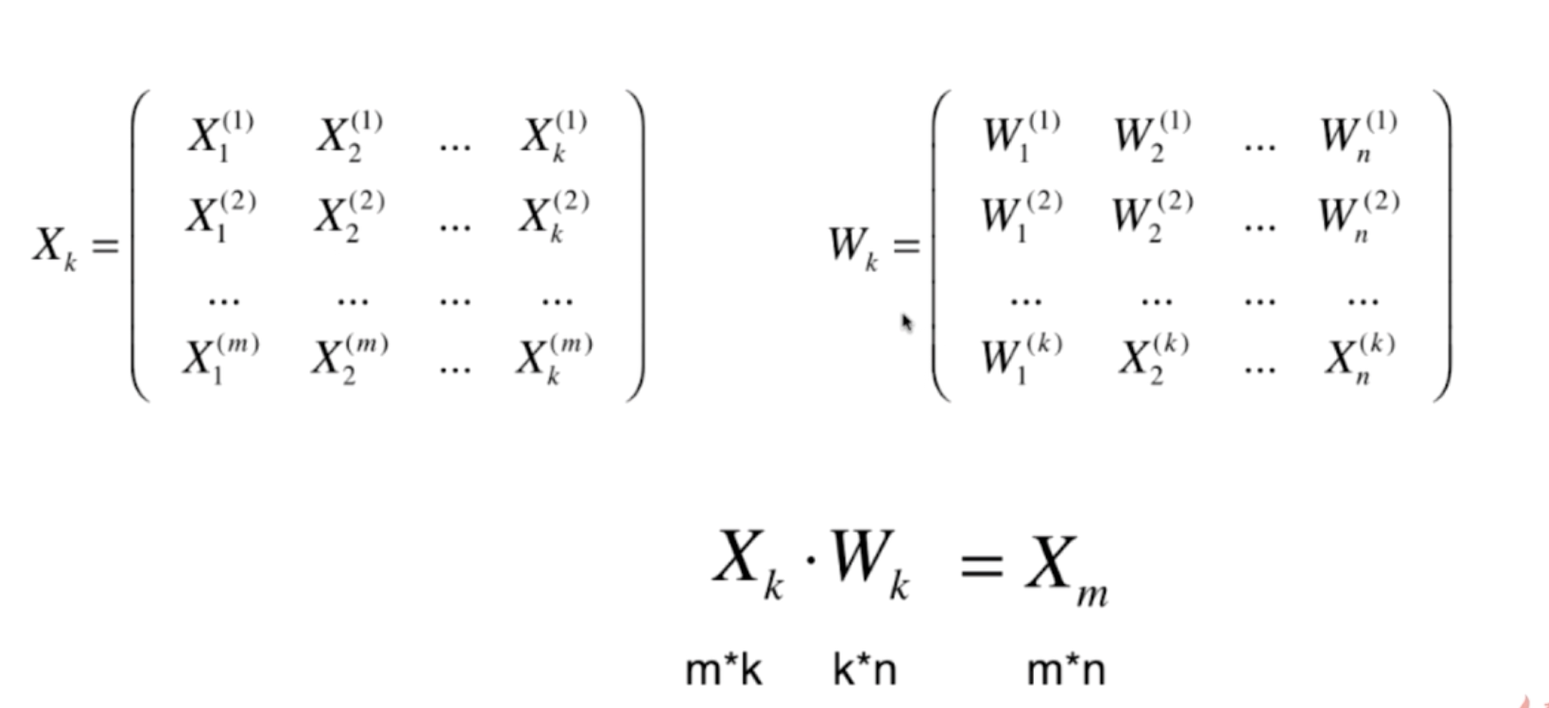
3、具体的数据降维实现原理代码如下所示:

import  numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.0,100.0,size=100)
x[:,1]=0.75*x[:,0]+3.0*np.random.normal(0,3,size=100)
plt.figure()
plt.scatter(x[:,0],x[:,1])
plt.show()

#demean操作函数定义
def demean(x):
    return x-np.mean(x,axis=0)
print(x)
print(np.mean(x,axis=0))
print(demean(x))
print(np.mean(demean(x),axis=0))
x_demean=demean(x)

#梯度上升法的函数定义
def f(w,x):
    return np.sum((x.dot(w))**2)/len(x)
def df_math(w,x):
    return x.T.dot(x.dot(w))*2/len(x)
def df_debug(w,x,epsilon=0.00001):
    res=np.empty(len(x))
    for i in range(len(x)):
        w1=w.copy()
        w1[i]=w1[i]+epsilon
        w2= w.copy()
        w2[i] =w2[i]-epsilon
        res[i]=(f(w1,x)-f(w2,x))/(2*epsilon)
    return res
def derection(w):
    return w/np.linalg.norm(w)
def gradient_ascent1(x,eta,w_initial,erro=1e-8, n=1e6):
    w=w_initial
    w=derection(w)
    i=0
    while i<n:
        gradient =df_math(w,x)
        last_w = w
        w = w + gradient * eta
        w = derection(w)   #注意1：每次都需要将w规定为单位向量
        if (abs(f(w,x) - f(last_w,x))) < erro:
            break
        i+=1
    return w
w0=np.random.random(x.shape[1])  #注意2：不能从0向量开始
print(w0)
eta=0.001     #注意3：不能将数据进行标准化，即不可以使用standardscaler进行数据标准化
w1=gradient_ascent1(x_demean,eta,w0)
print(w1)
q=np.linspace(-40,40)
Q=q*w1[1]/w1[0]
plt.figure(1)
plt.scatter(x[:,0],x[:,1])
plt.plot(q,Q,"r")
print(w1[1]/w1[0])

#求取数据的前n个的主成分，循环往复即可
x2=np.empty(x.shape)
for i in range(len(x)):
    x2[i]=x_demean[i]-x_demean[i].dot(w1)*w1
plt.figure()
plt.scatter(x2[:,0],x2[:,1],color="g")
plt.show()
w00=np.random.random(x.shape[1])
print(w00)
w2=gradient_ascent1(x2,eta,w00)
print(w2)

#求取n维数据的前n个主成分的封装函数
def first_n_compnent(n,x,eta=0.001,erro=1e-8, m=1e6):
    x_pca=x.copy()
    x_pca=demean(x_pca)
    res=[]
    for i in range(n):
        w0=np.random.random(x.shape[1])
        w=gradient_ascent1(x_pca,eta,w0)
        res.append(w)
        x_pca=x_pca-x_pca.dot(w).reshape(-1,1)*w
    return res
print(first_n_compnent(2,x))
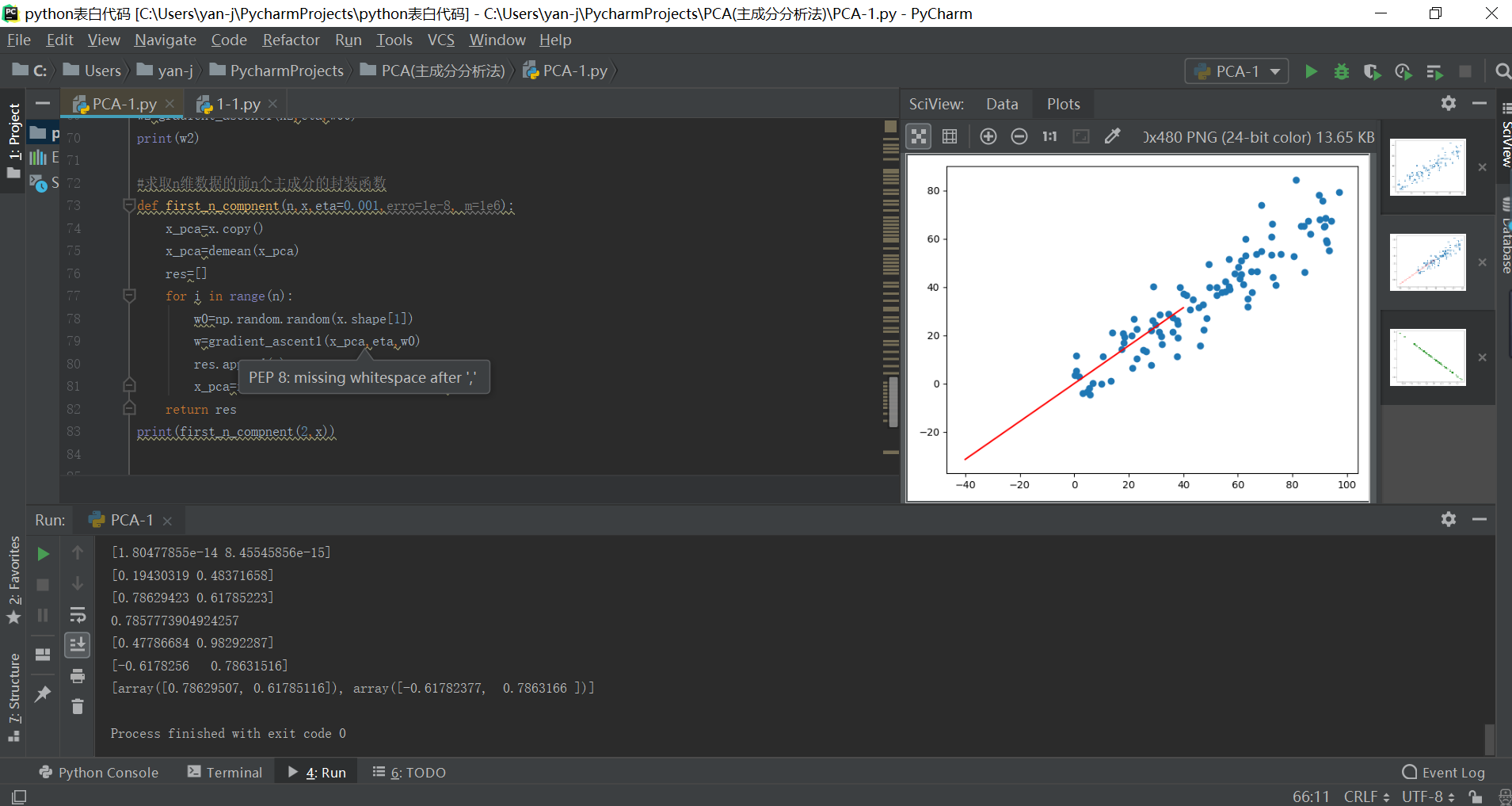
实际的运行效果如下所示：