机器学习梯度下降法的数学原理（非常易懂）

//2019.08.06
                                                               机器学习算法中的梯度下降法(gradient descent)
1、对于梯度下降法，具有以下几点特别说明：
(1)不是一种机器学习算法，不可以解决分类或者回归问题；
(2)是一种基于搜索的最优化方法；
(3)作用是最小化损失函数；
(4)梯度上升法：最大化效用函数。
2、梯度下降法就是在原来函数的基础上乘以一个步长，使得其整体始终为负值，然后从一个起始点开始走起来，一直到函数的极小值点处找到相应的最小值。

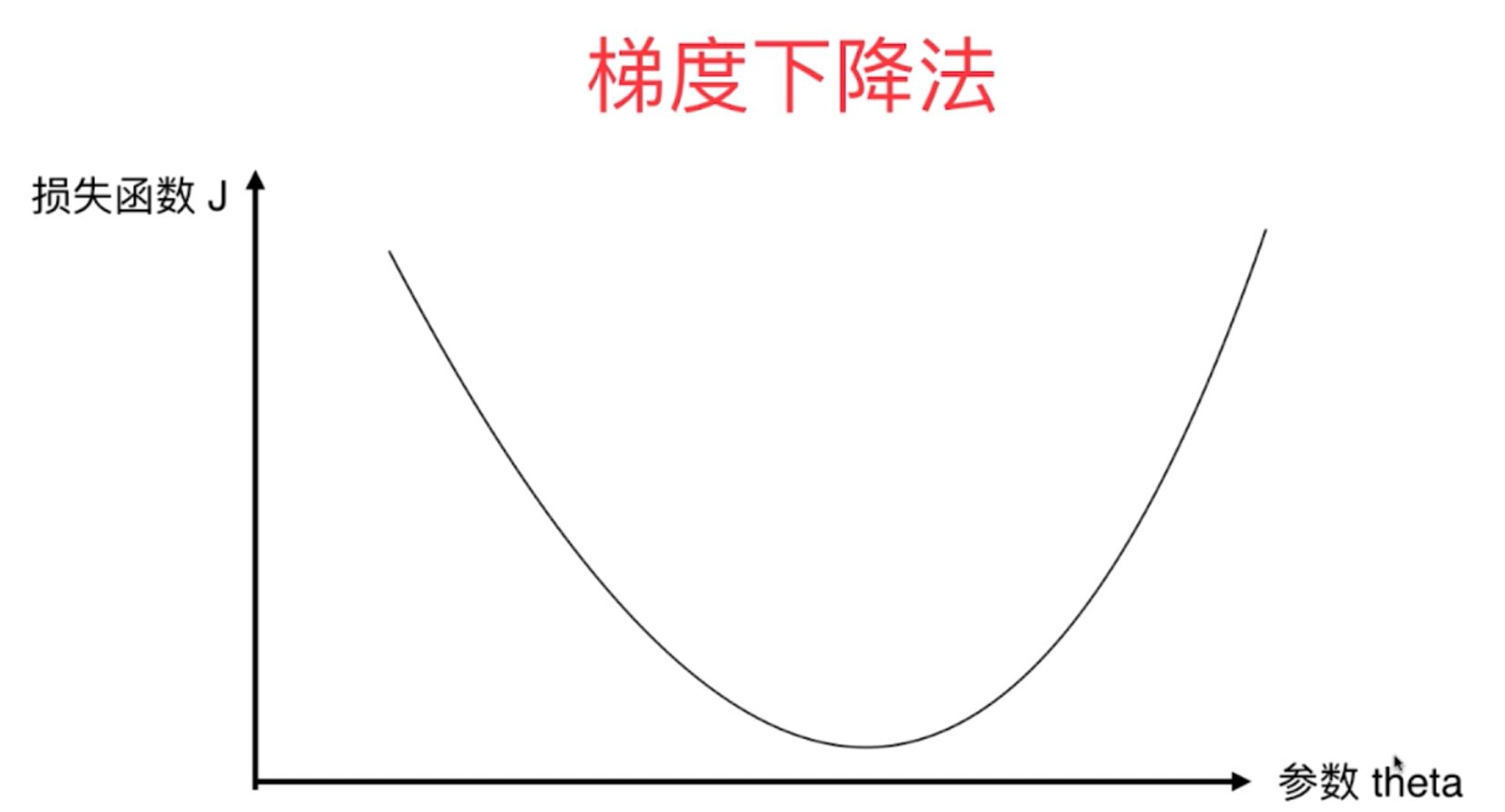
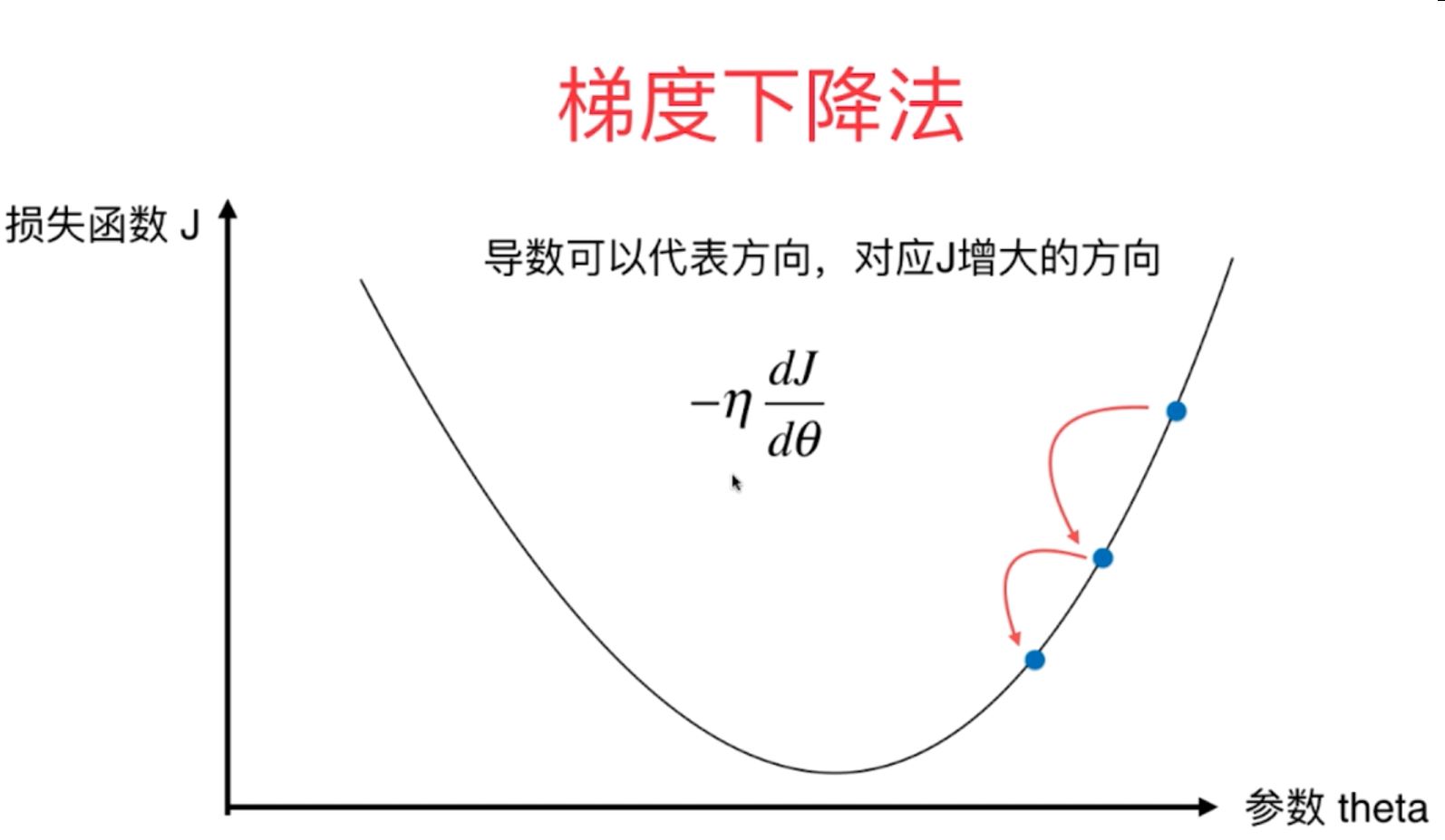
图1
3、对于步长η的取值，也叫作学习率，是一个0-1之间的数字，不能太大，也不能太小，原因是：
如果太大，则会减慢收敛学习的速度，如果太大，则容易导致不收敛。

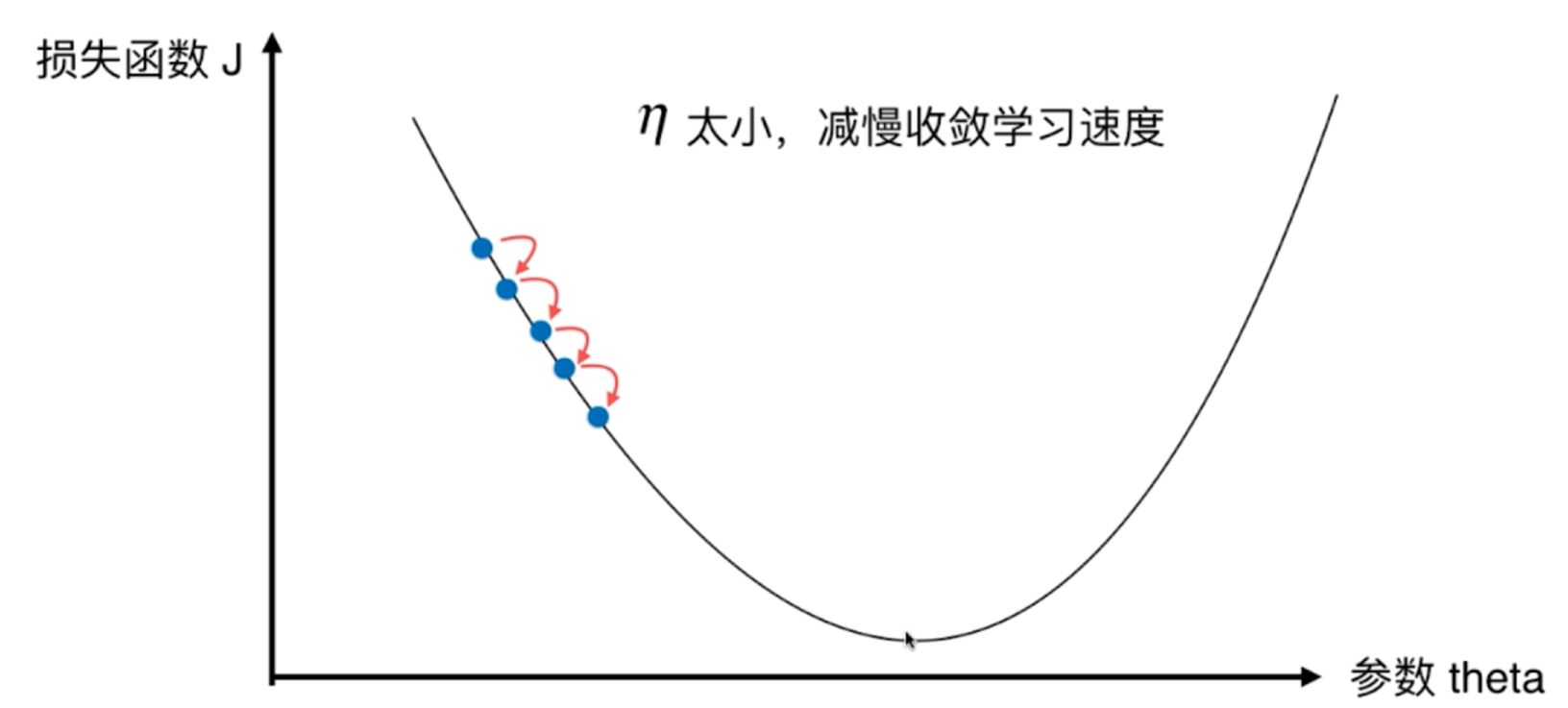
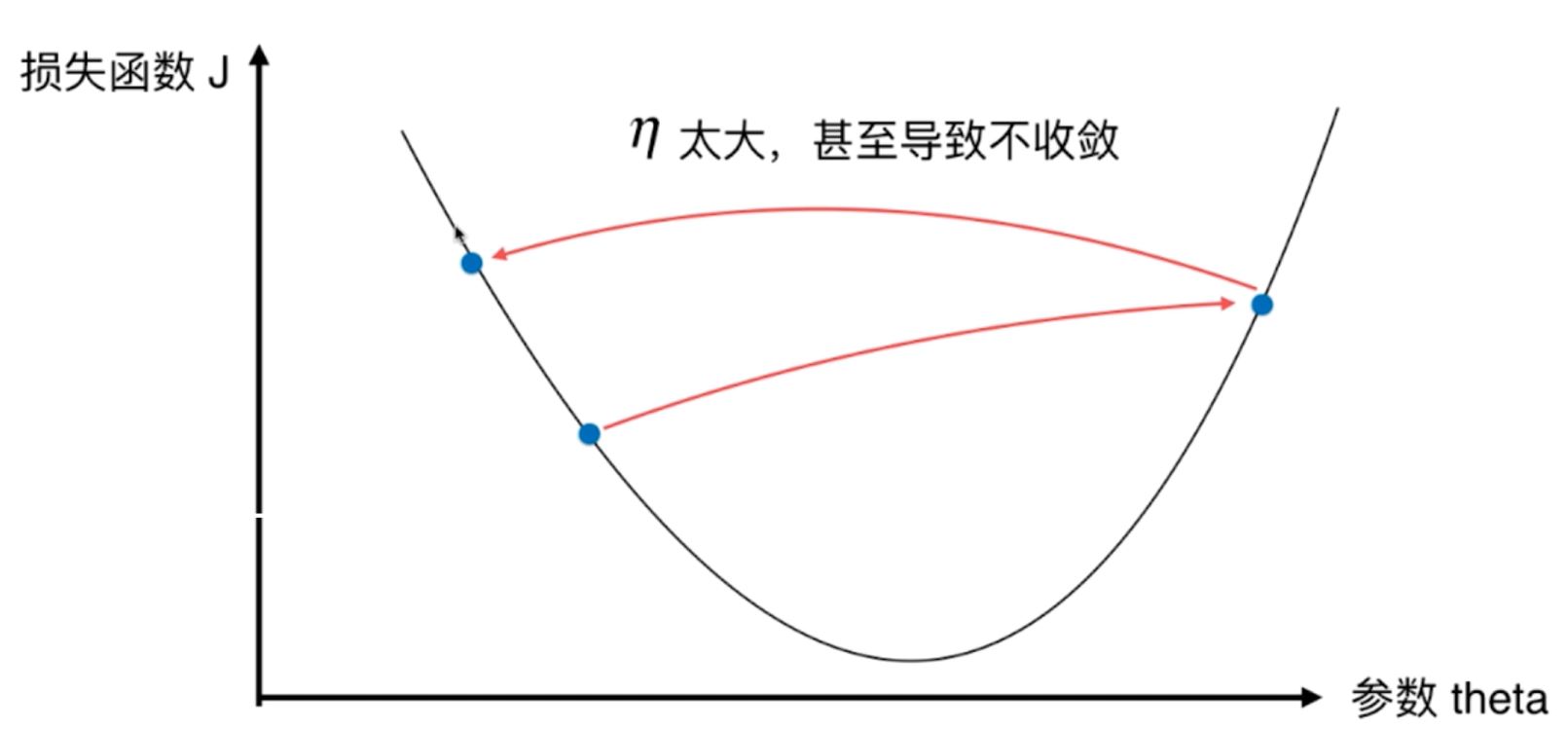
图2
4、对于梯度下降法的步长η，它称为学习率，具有以下特点：
(1)η的取值大小会影响取最优解的速度和效率；
(2)η取值不合适，甚至得不到最优解；
(3)η是梯度下降法的一个超参数。
5、对于梯度下降法的应用，并不一定所有的函数都有唯一的极小值，因此解决方案是：多次运行，随机化初始点，其初始点也是梯度下降法的一个超参数。

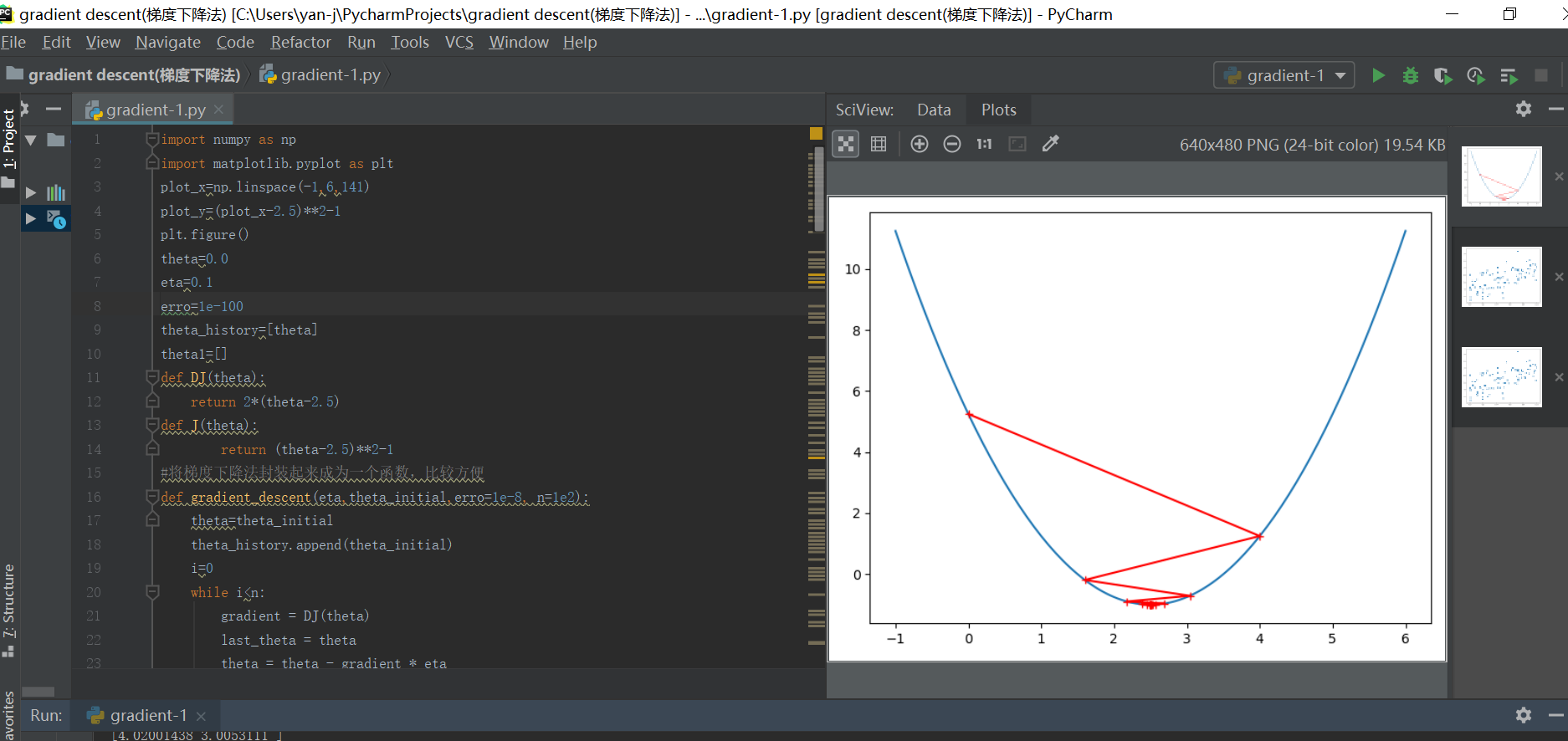
6、梯度下降法的python代码原理实现过程如下：
其中的函数以二次函数为例：

#1-1导入相应的模块
import numpy as np
import matplotlib.pyplot as plt

#1-2定义函数的相应变量取值范围为以及函数的表达式
plot_x=np.linspace(-1,6,141)
plot_y=(plot_x-2.5)**2-1
plt.figure()
theta=0.0
eta=0.1
erro=1e-100
theta_history=[theta]
theta1=[]
def DJ(theta):
return 2*(theta-2.5)
def J(theta):
return (theta-2.5)**2-1

###1-3将梯度下降法封装起来成为一个梯度下降函数，以便后续的使用和调节参数，使用起来比较方便
(其中最重要的超参数是1初始点的值x0，2梯度下降的定义步长eta,3最多的循环次数,4函数值的误差范围)
def gradient_descent(eta,theta_initial,erro=1e-8, n=1e2):
theta=theta_initial
theta_history.append(theta_initial)
i=0
while i<n:
gradient = DJ(theta)
last_theta = theta
theta = theta - gradient * eta
theta_history.append(theta)
if (abs(J(theta) - J(last_theta))) < erro:
break
i+=1
def plot_theta_history():
plt.plot(plot_x,plot_y)
plt.plot(np.array(theta_history),J(np.array(theta_history)),color="r",marker="+")
plt.show()

#1-4设置自己的初始超参数，直接进行结果的输出与相应的查询
eta=1.1
x0=0.0
theta_history=[]
gradient_descent(eta,x0)
plot_theta_history()
print(len(theta_history))
print(theta_history[-1])