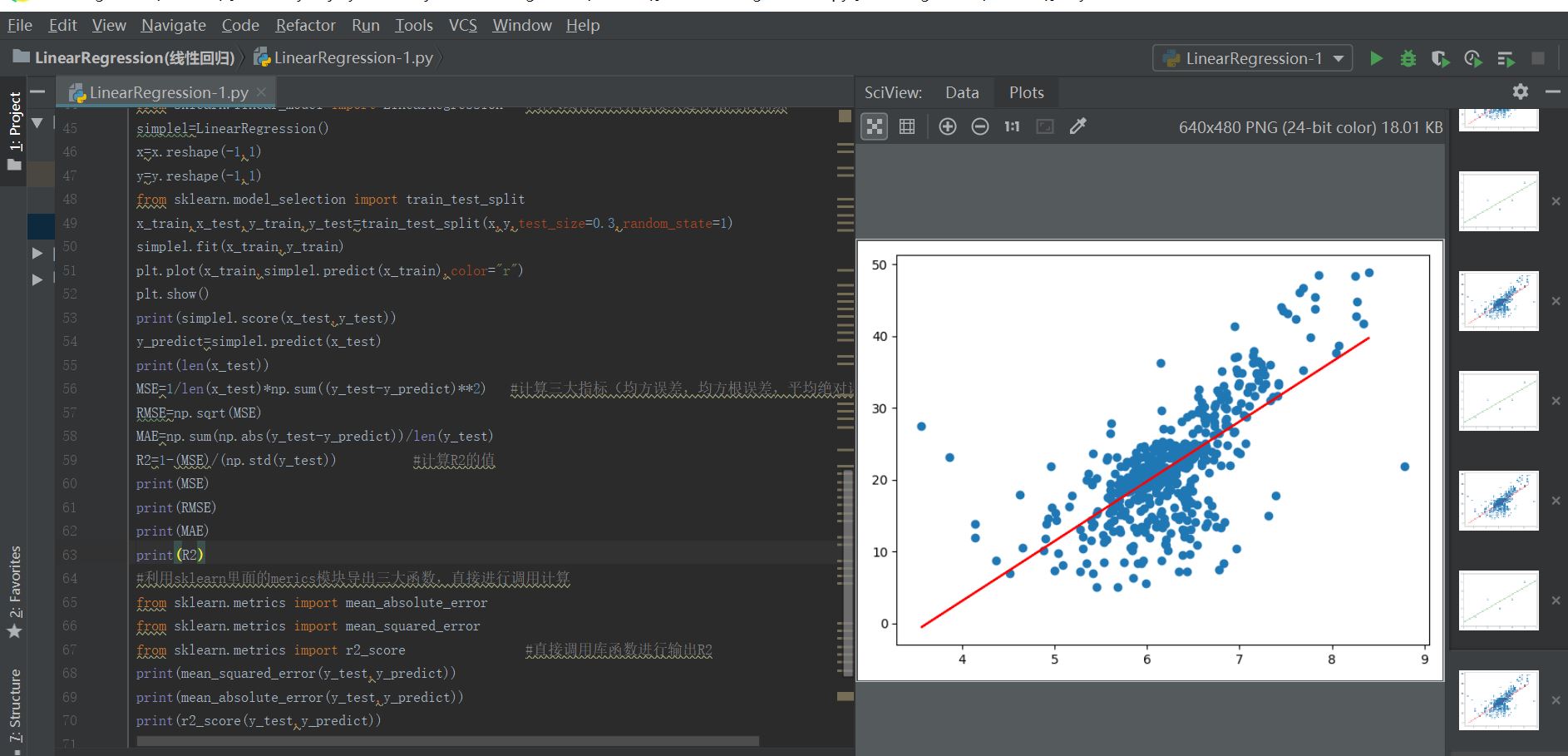
对于多元线性回归算法,它对于数据集具有较好的可解释性,我们可以对比不过特征参数的输出系数的大小来判断它对数据的影响权重,进而对其中隐含的参数进行扩展和收集,提高整体训练数据的准确性。
整体实现代码如下所示:
#1-1导入相应的基础数据集模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
d=datasets.load_boston()
print(d.data)
print(d.DESCR)
print(d.feature_names)
print(d.data[:,5])
x=d.data[d.target<50]
y=d.target[d.target<50]
#1-2使用多元线性回归法对其进行训练和预测
from sklearn.linear_model import LinearRegression #引入多元线性回归算法模块进行相应的训练
simple2=LinearRegression()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
simple2.fit(x_train,y_train)
print(simple2.coef_) #输出多元线性回归的各项系数
print(simple2.intercept_) #输出多元线性回归的常数项的值
y_predict=simple2.predict(x_test)
#1-3利用sklearn里面的merics模块导出三大评价指标进行评价,直接进行调用计算
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score #直接调用库函数进行输出R2
print(mean_squared_error(y_test,y_predict))
print(mean_absolute_error(y_test,y_predict))
print(r2_score(y_test,y_predict))
print(simple2.score(x_test,y_test))
print(simple2.coef_) #输出多元回归算法的各个特征的系数矩阵
print(np.argsort(simple2.coef_)) #输出多元线性回归算法各个特征的系数排序,可以知道各个特征的影响度
print(d.feature_names[np.argsort(simple2.coef_)]) #输出各个特征按照影响系数从小到大的顺序
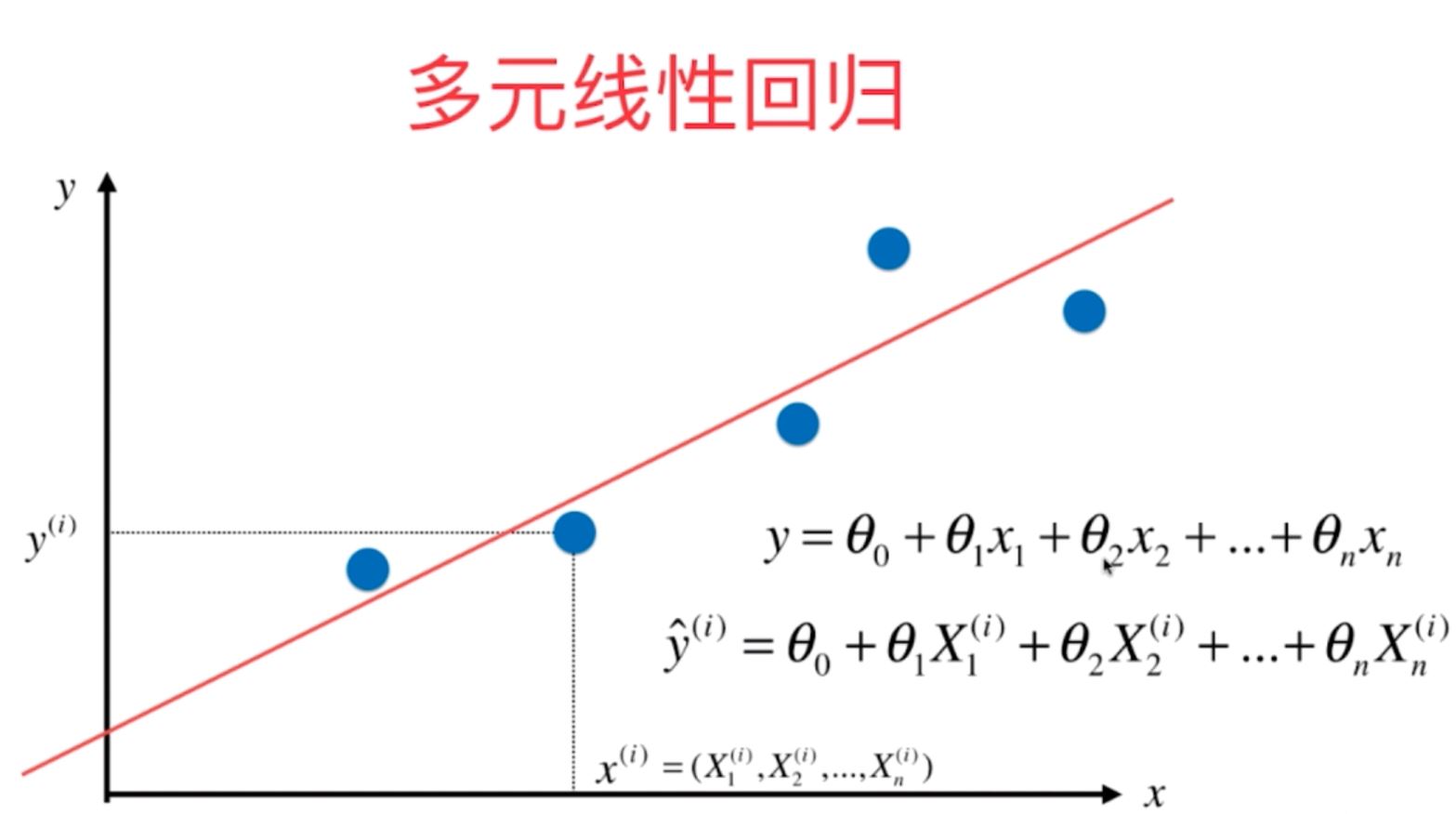
实现结果如下所示: