机器学习评价指标
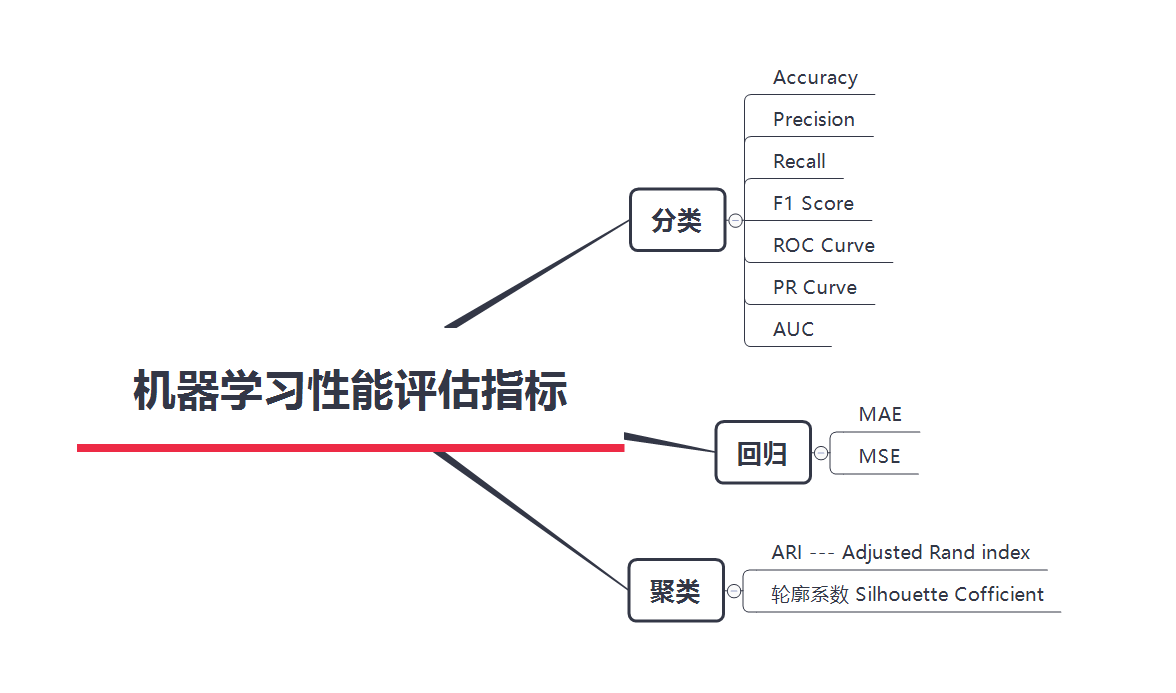

机器学习度量指标
分类评估指标
TN TP FN FP
TP:预测为正向(P),实际上预测正确(T),即判断为正向的正确率
TN:预测为负向(N),实际上预测正确(T),即判断为负向的正确率
FP:预测为正向(P),实际上预测错误(F),误报率,即把负向判断成了正向
FN:预测为负向(N),实际上预测错误(F),漏报率,即把正向判断称了负向
| Positive | Negative | |
|---|---|---|
| True | True Positive(TP) 真阳性 | True Negative(TN) 真阴性 |
| False | False Positive(FP) 假阳性 | False Negative(FN) 假阴性 |
准确率(Accuracy)
【注意】当分类问题是平衡(blanced)的时候,准确率可以较好地反映模型的优劣程度,但不适用于数据集不平衡的时候。
例如:分类问题的数据集中本来就有97% 示例是属于X,只有另外3%不属于X,所有示例都被分类成X的时候,准确率仍然高达97%,但这没有任何意义。
精确率Precision
查准率 即在预测为正向的数据中,有多少预测正确。【预测结果为真的数据】
召回率Recall
Recall=TP/(TP+FN)
查全率 即在所有正向的数据中,有多少预测正确。【样本原来真的数据】
F1-Score
F1值为精确率和召回率的调和均值。
ROC(Receiver Operating Characteristic)曲线
先了解以下几个概念
真正率(True Positive Rate, TPR),又名灵敏度(Sensitivity):分类正确的正样本个数占整个正样本个数的比例。
假负率(False Negative Rate, FNR):分类错误的正样本的个数占正样本的个数的比例。
假正率(False Positive Rate, FPR):分类错误的负样本个数占整个负样本个数的比例。
真负率(True Negative Rate, TNR):分类正确的负样本的个数占负样本的个数的比例。
ROC曲线是以假正率(FP_rate)和真正率(TP_rate)为轴的曲线,ROC曲线下面的面积我们叫做AUC。
AUC(Area Under Curve) 被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。
如下图所示:
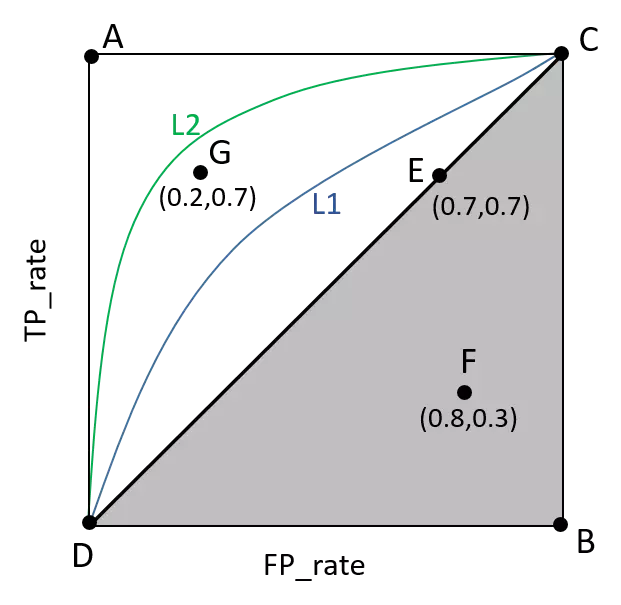
曲线与FP_rate轴围成的面积(记作AUC)越大,说明性能越好,即图上L2曲线对应的性能优于曲线L1对应的性能。即:曲线越靠近A点(左上方)性能越好,曲线越靠近B点(右下方)曲线性能越差。
PR(precision recall)曲线
表现的是precision和recall之间的关系。
回归评估指标
测试数据集中的点,距离模型的平均距离越小,该模型越精确。
使用平均距离,而不是所有测试样本的距离和,因为距离和受样本数量的影响
平均绝对误差 MAE
平均绝对误差MAE(Mean Absolute Error)又被称为 范数损失(l1-norm loss)。
平均平方误差 MSE
平均平方误差 MSE(Mean Squared Error)又被称为 范数损失(l2-norm loss)。
RMSE:均方根误差
均方根误差RMSE(Root Mean Squared Error)
RMSE和MAE有局限性:同一个算法模型,解决不同的问题,不能体现此模型针对不同问题所表现的优劣。因为不同实际应用中,数据的量纲不同,无法直接比较预测值,因此无法判断模型更适合预测哪个问题。
R-squared
-
原始数据和均值之差的平方和
-
预测数据与原始数据均值之差的平方和
上面公式中表示测试数据真实值的方差(内部差异);
代表回归值与真实值之间的平方差异(回归差异),因此R-squared既考量了回归值与真实值的差异,也兼顾了问题本身真实值的变动。【模型对样本数据的拟合度】
R-squared 取值范围,值越大表示模型越拟合训练数据;最优解是1;当模型 预测为随机值的时候,有可能为负;若预测值恒为样本期望,R2为0。
from sklearn.metrics import mean_squared_error #均方误差
from sklearn.metrics import mean_absolute_error #平方绝对误差
from sklearn.metrics import r2_score#R square
聚类性能指标
ARI (Adjusted Rand index)
若样本数据本身带有正确的类别信息,可用ARI指标进行评估。
from sklearn.metrics import adjusted_rand_score()
轮廓系数 Silhouette Cofficient
若样本数据没有所属类别,可用轮廓系数来度量聚类结果的质量。
from sklearn.metrics import silhouette_score
sklearn里的常见评测指标
| Scoring(得分) | Function(函数) | Comment(注解) |
|---|---|---|
| Classification(分类) | ||
| ‘accuracy’ | metrics.accuracy_score | |
| ‘average_precision’ | metrics.average_precision_score | |
| ‘f1’ | metrics.f1_score | for binary targets(用于二进制目标) |
| ‘f1_micro’ | metrics.f1_score | micro-averaged(微平均) |
| ‘f1_macro’ | metrics.f1_score | macro-averaged(微平均) |
| ‘f1_weighted’ | metrics.f1_score | weighted average(加权平均) |
| ‘f1_samples’ | metrics.f1_score | by multilabel sample(通过 multilabel 样本) |
| ‘neg_log_loss’ | metrics.log_loss | requires predict_proba support(需要 predict_proba 支持) |
| ‘precision’ etc. | metrics.precision_score | suffixes apply as with ‘f1’(后缀适用于 ‘f1’) |
| ‘recall’ etc. | metrics.recall_score | suffixes apply as with ‘f1’(后缀适用于 ‘f1’) |
| ‘roc_auc’ | metrics.roc_auc_score | |
| Clustering(聚类) | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score | |
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score | |
| ‘completeness_score’ | metrics.completeness_score | |
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score | |
| ‘homogeneity_score’ | metrics.homogeneity_score | |
| ‘mutual_info_score’ | metrics.mutual_info_score | |
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score | |
| ‘v_measure_score’ | metrics.v_measure_score | |
| Regression(回归) | ||
| ‘explained_variance’ | metrics.explained_variance_score | |
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error | |
| ‘neg_mean_squared_error’ | metrics.mean_squared_error | |
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error | |
| ‘neg_median_absolute_error’ | metrics.median_absolute_error | |
| ‘r2’ | metrics.r2_score |




