蓝桥杯历年真题JAVA版-2016年蓝桥杯省赛- Java组
第1题——生日蜡烛
(1)题目描述
某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。
现在算起来,他一共吹熄了236根蜡烛。
请问,他从多少岁开始过生日party的?
输出格式:请填写他开始过生日party的年龄数。
(2)解题代码
public static void func1() {
for (int i = 0; i < 100; i++) {
int sum = 0;// 一定要初始化 ,否则输出结果为0
for (int j = i;; j++) {
sum += j;// 从年龄i开始,往后累加一直加到要求的条件位置
if (sum > 236)// 若从年龄i累加,超过了236,终止循环
{
break;
}
if (sum == 236) {// 若从年龄i累加,刚好等于236,则开始吹蜡烛的年龄即为开始过生日的年龄。
System.out.println(i);
}
}
}
}(3)运行结果
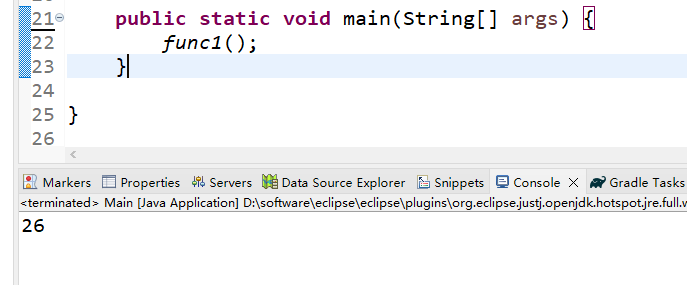
第2题——方格填数
(1)题目描述
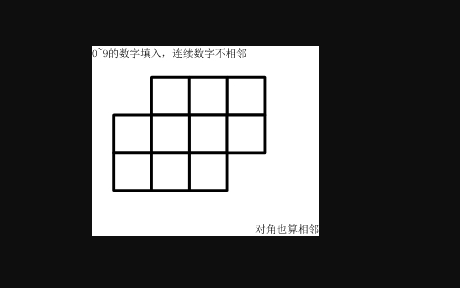
如下的10个格子,填入0~9的数字。要求:连续的两个数字不能相邻。
(左右、上下、对角都算相邻)一共有多少种可能的填数方案?
(2)解题代码
public static int[][] m = new int[3][4];
public static int[] pack = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
public static int[] visited = new int[10];
public static int sum = 0;
public static int solve() {
int ok = 1;
int index = 0;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if (m[i][j] == -2)
continue;
m[i][j] = pack[index];
index++;
}
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if (m[i][j] == -2)
continue;
if (i - 1 >= 0 && (m[i][j] == m[i - 1][j] + 1 || m[i][j] == m[i - 1][j] - 1))
return 0;
if (i + 1 < 3 && (m[i][j] == m[i + 1][j] + 1 || m[i][j] == m[i + 1][j] - 1))
return 0;
if (j - 1 >= 0 && (m[i][j] == m[i][j - 1] + 1 || m[i][j] == m[i][j - 1] - 1))
return 0;
if (j + 1 < 4 && (m[i][j] == m[i][j + 1] + 1 || m[i][j] == m[i][j + 1] - 1))
return 0;
if (i - 1 >= 0 && j - 1 >= 0 && (m[i][j] == m[i - 1][j - 1] + 1 || m[i][j] == m[i - 1][j - 1] - 1))
return 0;
if (i - 1 >= 0 && j + 1 < 4 && (m[i][j] == m[i - 1][j + 1] + 1 || m[i][j] == m[i - 1][j + 1] - 1))
return 0;
if (i + 1 < 3 && j - 1 >= 0 && (m[i][j] == m[i + 1][j - 1] + 1 || m[i][j] == m[i + 1][j - 1] - 1))
return 0;
if (i + 1 < 3 && j + 1 < 4 && (m[i][j] == m[i + 1][j + 1] + 1 || m[i][j] == m[i + 1][j + 1] - 1))
return 0;
}
}
return ok;
}
public static void dfs(int index) {
if (index == 10) {
if (solve() != 0) {
sum++;
}
} else {
for (int i = 0; i < 10; i++) {
if (visited[i] == 0) {
visited[i] = 1;
pack[index] = i;
dfs(index + 1);
visited[i] = 0;
}
}
}
}
public static void func2() {
for (int i = 0; i < 3; i++)
for (int j = 0; j < 4; j++)
m[i][j] = -1;
m[0][0] = -2;
m[2][3] = -2;
dfs(0);
System.out.println(sum);
}(3)运行结果
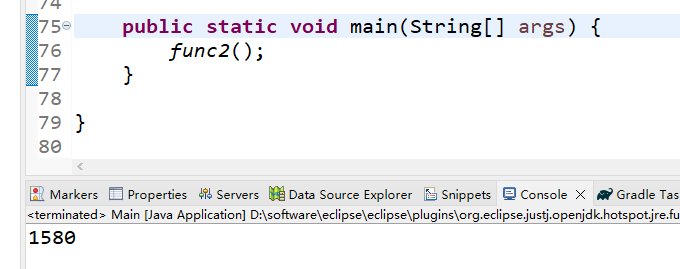
第3题——寒假作业
(1)题目描述
现在小学的数学题目也不是那么好玩的。
看看这个寒假作业:
每个方块代表1~13中的某一个数字,但不能重复。
比如:6 + 7 = 13以及:
9 - 8 = 1
3 * 4 = 12
10 / 2 = 57 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5就算两种解法。(加法,乘法交换律后算不同的方案)
你一共找到了多少种方案?
(2)解题代码
public static int[] a = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 };
public static int ans = 0;
public static void swap(int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void dfs(int m) {
if (m >= 13) {// + - * /
if (a[0] + a[1] == a[2] && a[3] - a[4] == a[5] && a[6] * a[7] == a[8] && a[9] / a[10] == a[11]
&& a[9] % a[10] == 0) {
if (ans < 10) {// 11/2==5
// System.out.println(a[0] + "+" + a[1] + "==" + a[2]);
// System.out.println(a[3] + "-" + a[4] + "==" + a[5]);
// System.out.println(a[6] + "*" + a[7] + "==" + a[8]);
// System.out.println(a[9] + "/" + a[10] + "==" + a[11]);
// System.out.println();
}
ans++;
}
return;
}
if (m >= 3 && a[0] + a[1] != a[2])// 剪枝,2^13跑不出来
return;
if (m >= 6 && a[3] - a[4] != a[5])// 这个剪不剪都行反正跑出来了
return;
for (int i = m; i < 13; i++) {
swap(m, i);
dfs(m + 1);
swap(m, i);
}
}
public static void func3() {
dfs(0);
System.out.println(ans);
}(3)运行结果
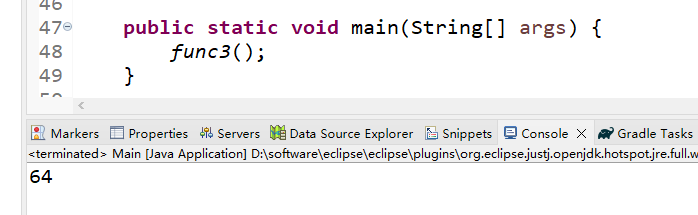
第4题——剪邮票
(1)题目描述
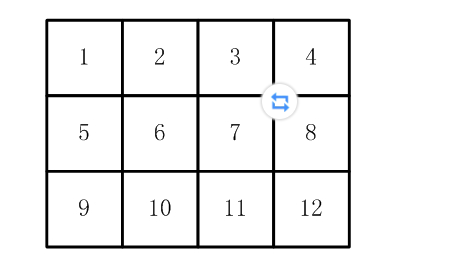
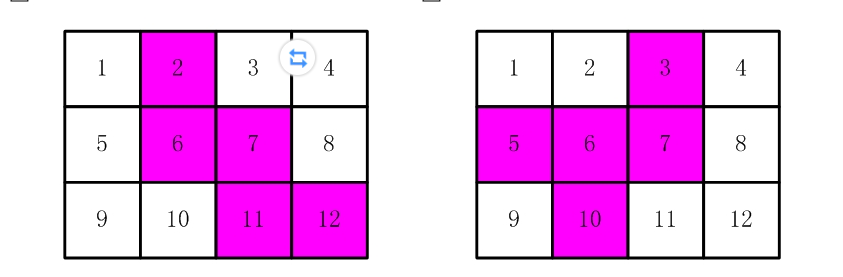
如下图, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来,要求必须是连着的。(仅仅连接一个角不算相连)
比如,下面两张图中,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
(2)解题代码
public static boolean[] book = new boolean[12];
public static int[] path = new int[5];
public static int[][] map = new int[3][4];
public static Set<String> set = new HashSet<String>();
public static int ans;
public static void dfs(int index) {
if (index == 5) {
int[] tmp = Arrays.copyOf(path, 5);
Arrays.sort(tmp);
String str = tmp[0] + "" + tmp[1] + "" + tmp[2] + "" + tmp[3] + "" + tmp[4];
if (!set.contains(str) && check()) {
set.add(str);
ans++;
}
} else {
for (int i = 0; i < 12; i++) {
if (!book[i]) {
book[i] = true;
path[index] = i;
dfs(index + 1);
book[i] = false;
}
}
}
}
public static boolean check() {
map = new int[3][4];
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
for (int t = 0; t < 5; t++) {
if (i * 4 + j == path[t]) {
map[i][j] = 1;
}
}
}
}
int cnt = 0;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if (map[i][j] == 1) {
dfs_connect(i, j);
cnt++;
}
}
}
return cnt == 1;
}
public static void dfs_connect(int i, int j) {
map[i][j] = 0;
if (i + 1 < 3 && map[i + 1][j] == 1)
dfs_connect(i + 1, j);
if (j + 1 < 4 && map[i][j + 1] == 1)
dfs_connect(i, j + 1);
if (i - 1 >= 0 && map[i - 1][j] == 1)
dfs_connect(i - 1, j);
if (j - 1 >= 0 && map[i][j - 1] == 1)
dfs_connect(i, j - 1);
}
public static void func4() {
dfs(0);
System.out.println(ans);
}
(3)运行结果
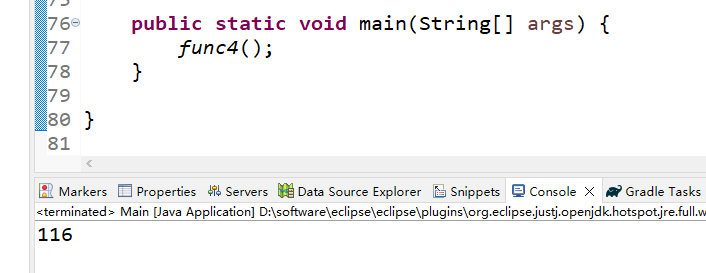
第5题——四平方和
(1)题目描述
四平方和定理,又称为拉格朗日定理:每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去,就正好可以表示为4个数的平方和。
比如:
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2(^符号表示乘方的意思)
对于一个给定的正整数N,可能存在多种平方和的表示法。
要求你对4个数排序:0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法输入格式:
输入存在多组测试数据,每组测试数据输入一行为一个正整数N (N<5000000)输出格式:
对于每组测试数据,要求输出4个非负整数,按从小到大排序,中间用空格分开输入样例:
5
12
773535
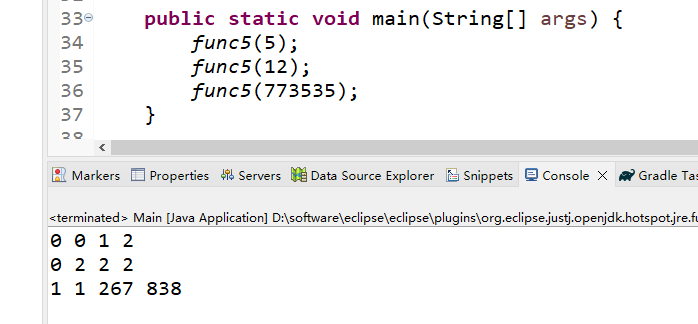
输出样例:
0 0 1 2
0 2 2 2
1 1 267 838
(2)解题代码
public static void func5(int n) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int c = 0; c * c <= n / 2; c++) {
for (int d = c; d * d + c * c <= n; d++) {
// 用map保存值和对应的a
if (map.containsKey(c * c + d * d) == false) {
map.put(c * c + d * d, c);
}
}
}
for (int a = 0; a * a <= n / 4; a++) {
for (int b = a; b * b + a * a <= n / 2; b++) {
if (map.containsKey(n - (b * b + a * a))) {
int c = (int) map.get(n - (a * a + b * b));
int d = (int) Math.sqrt(n - (b * b + c * c) - a * a);
System.out.printf("%d %d %d %d\n", a, b, c, d);
return;
}
}
}
}(3)运行结果
第6题——密码脱落
(1)题目描述
X星球的考古学家发现了一批古代留下来的密码。这些密码是由A、B、C、D 四种植物的种子串成的序列。
仔细分析发现,这些密码串当初应该是前后对称的(也就是我们说的镜像串)。
由于年代久远,其中许多种子脱落了,因而可能会失去镜像的特征。
你的任务是:给定一个现在看到的密码串,计算一下从当初的状态,它要至少脱落多少个种子,才可能会变成现在的样子。输入格式:
输入存在多组测试数据,对于每组测试数据输入一行,表示现在看到的密码串(长度不大于1000)输出格式:
对于每组测试数据要求输出一个正整数,表示至少脱落了多少个种子。输入样例 :
ABCBA
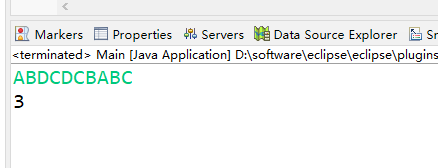
ABDCDCBABC输出样例:
0
3
(2)解题代码
public static int min = 0, num = 0;
public static String inputstr;
public static void fcode(int left, int right, int num) {
if (left >= right) {
min = min < num ? min : num; // 每次递归结束都会得到一个num,与全局变量min对比更新,最终得到最小值
} else {
if (inputstr.charAt(left) == inputstr.charAt(right)) // 左右对比是否一致
fcode(left + 1, right - 1, num);
else {
fcode(left + 1, right, num + 1); // 左边+1
fcode(left, right - 1, num + 1); // 右边-1
}
}
return;
}
public static void func8() {
// 层数
Scanner in = new Scanner(System.in);
inputstr = in.next();
min = inputstr.length();
fcode(0, min - 1, 0);
System.out.println(min);
in.close();
}(3)运行结果

第7题——煤球数目
(1)题目描述
有一堆煤球,堆成三角棱锥形。具体:
第一层放1个,
第二层3个(排列成三角形),
第三层6个(排列成三角形),
第四层10个(排列成三角形),
....
如果一共有100层,共有多少个煤球?输出格式:
请填表示煤球总数目的数字。
(2)解题代码
public static void func7() {
// 层数
int c = 0;
int sum = 0;
for (int i = 1; i <= 100; i++) {
// 统计每层的个数
c += i;
// 上层加上这层个数
sum += c;
}
System.out.println(sum);
}(3)运行结果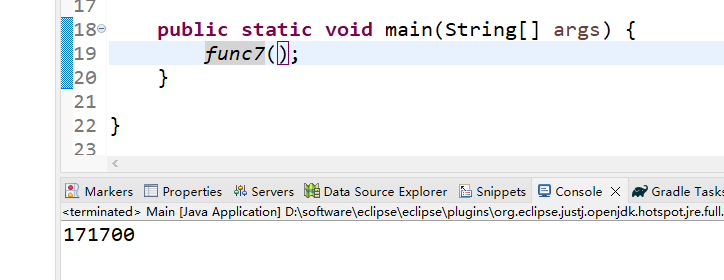
第8题——凑算式
(1)题目描述
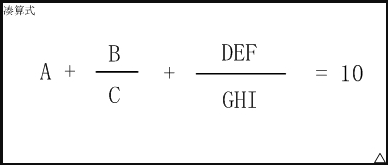
这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,5+3/1+972/486 是另一种解法。
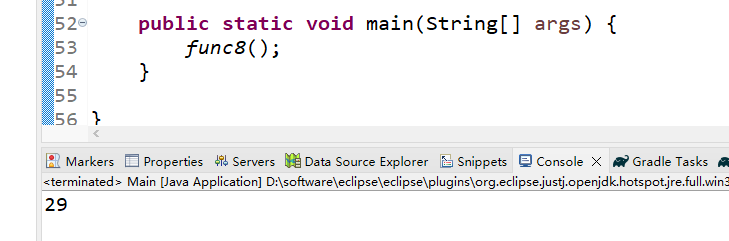
这个算式一共有多少种解法?输出格式:
输出一个整数表示答案
(2)解题代码
public static void func8() {
int x = 0;// 保存结果
int[] nums = new int[9];// 用于验证结果数据,
for (int i = 1; i < 10; i++) {// 第1个数A
for (int j = 1; j < 10; j++) {// 第2个数B
for (int k = 1; k < 10; k++) {// 第3个数C
for (int l = 123; l <= 987; l++) {// 被除数DEF
for (int m = 123; m <= 987; m++) {// 除数GHI
double z = i * 1.0 + j * 1.0 / k * 1.0 + l * 1.0 / m * 1.0;
// 验证结果是否等于10,等于10后将数据存入数组中验证是否为1-9.
if (z == 10.0) {
// 数据存入数组
nums[0] = i;
nums[1] = j;
nums[2] = k;
nums[3] = l % 10;
nums[4] = (l / 10) % 10;
nums[5] = (l / 100) % 10;
nums[6] = m % 10;
nums[7] = (m / 10) % 10;
nums[8] = (m / 100) % 10;
// 验证数组值是否为1-9
Arrays.sort(nums);
boolean flag = true;
for (int n = 0; n < 9; n++) {
if (n + 1 != nums[n]) {
flag = false;
break;
}
}
// 符合要求计数器+1
if (flag) {
x++;
}
}
}
}
}
}
}
// 输出结果
System.out.println(x);
}(3)运行结果
第9题——交换瓶子
(1)题目描述
有N个瓶子,编号 1 ~ N,放在架子上。
比如有5个瓶子:2 1 3 5 4,要求每次拿起2个瓶子,交换它们的位置。
经过若干次后,使得瓶子的序号为:1 2 3 4 5
对于这么简单的情况,显然,至少需要交换2次就可以复位。
如果瓶子更多呢?你可以通过编程来解决。输入格式:
输入存在多组测试数据,对于每组测试数据:
第一行: 一个正整数N(N<10000), 表示瓶子的数目
第二行:N个正整数,用空格分开,表示瓶子目前的排列情况。输出格式:
对于每组测试数据输出一行,包含一个正整数表示答案输入样例:
5
3 1 2 5 4
5
5 4 3 2 1输出样例:
3
2
(2)解题代码
public static int[] bottle;
public static int count = 0;
public static void swap(int a, int b) {
int tmp = bottle[a];
bottle[a] = bottle[b];
bottle[b] = tmp;
}
public static void func9() {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
bottle = new int[n + 1];
for (int i = 1; i <= n; i++)
bottle[i] = in.nextInt();
for (int i = 1; i <= n; i++) {
while (i != bottle[i]) {
swap(i, bottle[i]);
count++;
}
}
System.out.println(count);
in.close();
}(3)运行结果
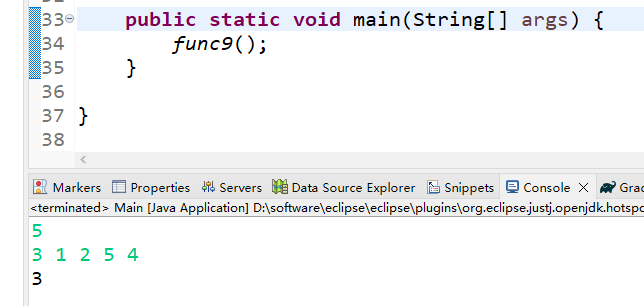

第10题——平方怪圈
(1)题目描述
如果把一个正整数的每一位都平方后再求和,得到一个新的正整数。对新产生的正整数再做同样的处理。
如此一来,你会发现,不管开始取的是什么数字,最终如果不是落入1,就是落入同一个循环圈。
请写出这个循环圈中最大的那个数字。输出格式:
输出答案即可
(2)解题代码
/*
* 定义一个方法输出循环圈中最大值
*/
public static int m(int num) {
int max = 0;// 记录最大值
while (true) {
int temp = 0;// 平方和
while (num != 0) {
temp += Math.pow((num % 10), 2);
num = num / 10;
}
if (max == temp) {
break;
} else {
// 最大值
max = (max > temp) ? max : temp;
num = temp;// 再循环
}
}
return max;
}
public static void func10() {
Random r = new Random();
int a = r.nextInt(100);// 产生一个100以内的随机数
System.out.println(m(a));// 输出最大值
}(3)运行结果
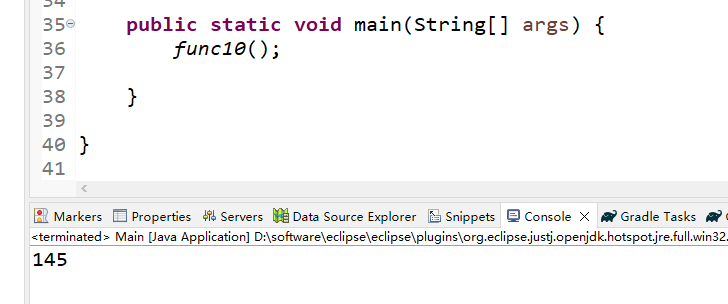
第11题——冰雹数
(1)题目描述
任意给定一个正整数N,如果是偶数,执行: N / 2;如果是奇数,执行: N * 3 + 1
生成的新的数字再执行同样的动作,循环往复。
通过观察发现,这个数字会一会儿上升到很高,一会儿又降落下来。
就这样起起落落的,但最终必会落到“1”
这有点像小冰雹粒子在冰雹云中翻滚增长的样子。
比如N=9:9,28,14,7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1
可以看到,N=9的时候,这个“小冰雹”最高冲到了52这个高度。输入格式:
输入存在多组测试数据,对于每组测试数据输入一行包含一个正整数N(N<1000000)输出格式:
对于每组测试数据,输出一行包含一个正整数表示答案输入样例:
10
100输出样例:
52
9232
(2)解题代码
public static void func11(int n) {
int max = 0;
int b;
for (int i = 1; i <= n; i++) { // 一个正整数表示不大于N的数 //所有小于N的数都要循环
b = i;
while (b != 1) {
if (b % 2 == 0) {
b /= 2;
} else {
b = b * 3 + 1;
}
if (b >= max) {
max = b;
}
}
}
System.out.println(max);
}(3)运行结果
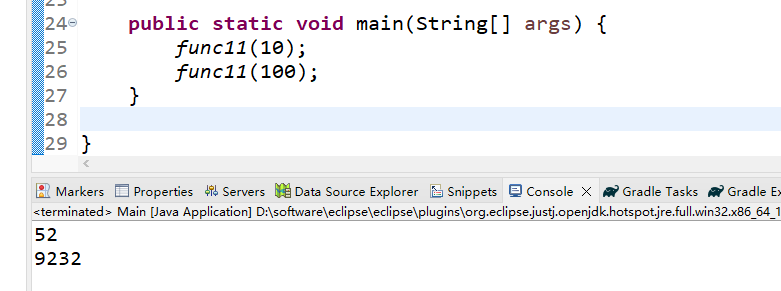
第12题——搭积木
(1)题目描述
小明最近喜欢搭数字积木,一共有10块积木,每个积木上有一个数字,0~9。
搭积木规则:每个积木放到其它两个积木的上面,并且一定比下面的两个积木数字小。
最后搭成4层的金字塔形,必须用完所有的积木
下面是两种合格的搭法:0
1 2
3 4 5
6 7 8 90
3 1
7 5 2
9 8 6 4请你计算这样的搭法一共有多少种?
输出格式:
一个整数表示答案
(2)解题代码
public static int count = 0;
public static void dfs(int[] arr, int num, int k) {
if (num == k) {
if (panDuan(arr)) {
count++;
}
}
for (int i = num; i < arr.length; i++) {
swap(arr, num, i);
dfs(arr, num + 1, k);
swap(arr, num, i);
}
}
public static void swap(int[] arr, int num, int i) {
int temp = arr[num];
arr[num] = arr[i];
arr[i] = temp;
}
public static boolean panDuan(int[] arr) {
if (arr[0] < arr[1] && arr[0] < arr[2]) {
if (arr[1] < arr[3] && arr[1] < arr[4]) {
if (arr[2] < arr[4] && arr[2] < arr[5]) {
if (arr[3] < arr[6] && arr[3] < arr[7]) {
if (arr[4] < arr[7] && arr[4] < arr[8]) {
if (arr[5] < arr[8] && arr[5] < arr[9]) {
return true;
}
}
}
}
}
}
return false;
}
public static void func12() {
int arr[] = new int[] { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
dfs(arr, 0, 10);
System.out.println(count);
}
(3)运行结果

第13题——取球博弈
(1)题目描述
两个人玩取球的游戏。一共有N个球,每人轮流取球,每次可取集合{n1,n2,n3}中的任何一个数目。
如果无法继续取球,则游戏结束。此时,持有奇数个球的一方获胜。如果两人都是奇数,则为平局。
假设双方都采用最聪明的取法,第一个取球的人一定能赢吗?试编程解决这个问题。输入格式:
输入存在多组测试样例,对于每一组测试数据:
第一行3个正整数n1 n2 n3,空格分开,表示每次可取的数目 (0<n1,n2,n3<100)
第二行5个正整数x1 x2 ... x5,空格分开,表示5局的初始球数(0<xi<1000)输出格式:
一行5个字符,空格分开。分别表示每局先取球的人能否获胜。
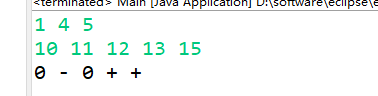
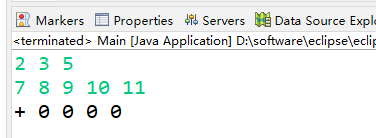
能获胜则输出+,次之,如有办法逼平对手,输出0,无论如何都会输,则输出-输入样例:
1 2 3
1 2 3 4 5
1 4 5
10 11 12 13 15
2 3 5
7 8 9 10 11输出样例:
+ 0 + 0 -
0 - 0 + +
+ 0 0 0 0
(2)解题代码
public static int[] n;
public static char[][][] cache = new char[1000][2][2];
/**
*
* @param num 球的总数
* @param me 我方持有的数目-->我方数目的奇偶性
* @param you 对手持有的数目-对方数目的奇偶性
* @return
*/
public static char f(int num, int me, int you) {
if (num < n[0]) {
if ((me & 1) == 1 && (you & 1) == 0) {
return '+';
} else if ((me & 1) == 0 && (you & 1) == 1) {
return '-';
} else {
return '0';
}
}
if (cache[num][me][you] != '\0')
return cache[num][me][you];
boolean flag = false;
for (int i = 0; i < 3; i++) {
if (num >= n[i]) {
char res = f(num - n[i], you, (n[i] & 1) == 0 ? me : (1 - me));// 注意此处,传递me和you的奇偶性
if (res == '-') {
cache[num][me][you] = '+';
return '+';
}
if (res == '0') {
flag = true;
}
}
}
// 如果能走到第这行,说明不存在对手输的情况,那么是否存在平的情况
if (flag) {
cache[num][me][you] = '0';
return '0';
} else {
cache[num][me][you] = '-';
return '-';
}
}
public static void func13() {
Scanner in = new Scanner(System.in);
n = new int[3];
for (int i = 0; i < 3; i++) {
n[i] = in.nextInt();
}
Arrays.sort(n);// 排序
for (int i = 0; i < 5; i++) {
int num = in.nextInt();
char res = f(num, 0, 0);
System.out.print(res + " ");
}
System.out.println();
in.close();
}(3)运行结果
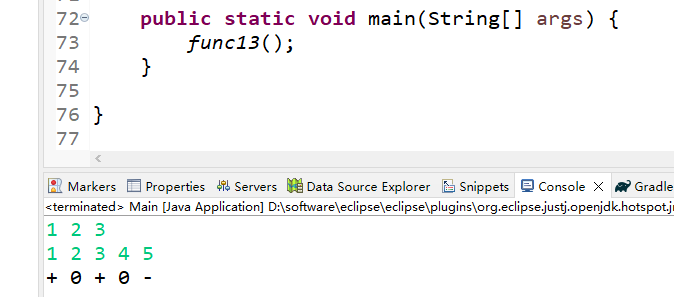
第14题——压缩变换
(1)题目描述
小明最近在研究压缩算法。他知道,压缩的时候如果能够使得数值很小,就能通过熵编码得到较高的压缩比。然而,要使数值很小是一个挑战。
最近,小明需要压缩一些正整数的序列,这些序列的特点是,后面出现的数字很大可能是刚出现过不久的数字。对于这种特殊的序列,小明准备对序列做一个变换来减小数字的值。
变换的过程如下:
从左到右枚举序列,每枚举到一个数字,如果这个数字没有出现过,刚将数字变换成它的相反数,如果数字出现过,则看它在原序列中最后的一次出现后面(且在当前数前面)出现了几种数字,用这个种类数替换原来的数字。
比如,序列(a1, a2, a3, a4, a5)=(1, 2, 2, 1, 2)在变换过程为:
a1: 1未出现过,所以a1变为-1;
a2: 2未出现过,所以a2变为-2;
a3: 2出现过,最后一次为原序列的a2,在a2后、a3前有0种数字,所以a3变为0;
a4: 1出现过,最后一次为原序列的a1,在a1后、a4前有1种数字,所以a4变为1;
a5: 2出现过,最后一次为原序列的a3,在a3后、a5前有1种数字,所以a5变为1。
现在,给出原序列,请问,按这种变换规则变换后的序列是什么。
输入格式:
输入第一行包含一个整数n,表示序列的长度。第二行包含n个正整数,表示输入序列a。
1 <=n<=100000,1<=ai<=10^9
输出格式:
对于每组测试数据,输出一行,包含n个数,表示变换后的序列。
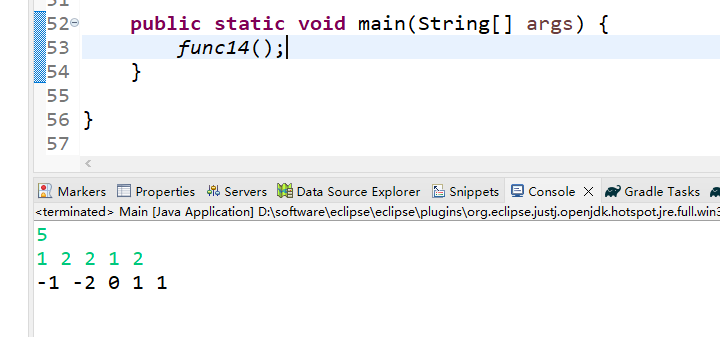
输入样例:
5
1 2 2 1 2
输出样例:
-1 -2 0 1 1
(2)解题代码
public static void func14() {
Scanner in = new Scanner(System.in);
int n;
n = in.nextInt();
int[] a = new int[n + 1];// 输入用的
int[] b = new int[1000 * 100 + 1];// 判断用的,不占多少内存,暴力杯嘛
int[] c = new int[n + 1];// 存结果用的
for (int i = 1; i < n + 1; i++) {
a[i] = in.nextInt();
}
for (int i = 1; i < n + 1; i++) {
if (b[a[i]] == 0) {// 如果没出现过,则变为负
c[i] = -a[i];// 存值
} else {
int k = i - b[a[i]] - 1;
if (k == 0) {
c[i] = 0;
} else if (k == 1)
c[i] = 1;
else {
int[] s = new int[k];// 创建数组s
for (int l = 0; l < k; l++) {
s[l] = a[b[a[i]] + 1 + l];// 抠出中间段
}
Arrays.sort(s);// sort一下啊
int counts = 1;// 计数君,因为循环从1开始,判断这个与前一个,所以起始为1
for (int l = 1; l < k; l++) {// 统计不同的个数
if (s[l] == s[l - 1]) {
continue;
} else
counts++;
}
c[i] = counts;
}
}
b[a[i]] = i;// 记录最后下标位置
}
System.out.print(c[1]);// 第一个不带空格
for (int i = 2; i < n + 1; i++) {// 后面的带空格
System.out.print(" " + c[i]);
}
in.close();
}(3)运行结果
第15题——有奖猜谜
(1)题目描述
小明很喜欢猜谜语。最近,他被邀请参加了X星球的猜谜活动。
每位选手开始的时候都被发给777个电子币。
规则是:猜对了,手里的电子币数目翻倍,猜错了,扣除555个电子币, 扣完为止。
小明一共猜了15条谜语。战果为:vxvxvxvxvxvxvvx
其中v表示猜对了,x表示猜错了。请你计算一下,小明最后手里的电子币数目是多少。
输出格式:请填写表示最后电子币数目的数字。
(2)解题代码
public static void func15() {
String s = "vxvxvxvxvxvxvvx";
char[] ch = s.toCharArray();
int a = 777;
for (int i = 0; i < ch.length; i++) {
if (ch[i] == 'v') {
a *= 2;
} else {
a -= 555;
}
}
System.out.println(a);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号