倍增算法 LCA RMQ

啥是倍增思想？

倍增，每次将范围扩大或减少一倍而达到加速的效果

举个栗子，你想要跳到15米远的地方，你怎么找到这个15这个地方，一步一步跳吗，利用倍增的话

预设一个k使2^k>15值 ，这里我们假设k=5，

2^5=32 >15 k--; k=4; 跳过了，不跳

2^4=16 >15 k--; k=3; 跳过了，不跳

2^3=8 <=15 n=15-8=7; k--; k=2; 没跳到，可以跳

2^2=4 <= 7 n=7-4=3 ; k-- ; k=1;没跳到，可以跳

2^1=2 <= 3 n=3-2=1 ; k-- ; k=0;没跳到，可以跳

2^0=1 <= 1 n=1-1=0; 跳到了，停

这样我们只跳了4次，与朴素的15次相比，优化了11次！而且随着数据越来越大，这就是O(n) 和 O(logn)的区别了

因为每一个数都可以由二进制来表示，所以每一个距离我们都可以把他拆分成几个 2^k 相加的形式

觉得倍增很像是二分的逆过程（自底向上的二分），二分是对一个很大的区间折半的查找看当前是否成立，是用一个值去对应区间，利用值不停的缩小区间，而倍增是利用二进制的思想用区间去对应一个值，一个区间一个区间的减少去逼近一个值，虽然没有什么卵用，但是感觉很神奇，你品，你细品

关于倍增思想的总结

兔子跳：很多时候，倍增思想的使用过程就像兔子跳跃的过程一样（设兔子单次跳跃的距离为，假设在每次跳跃完成后，）.学习这只兔子的跳跃过程，我们就可以尝试把极高的时间复杂度优化成

对数据查询的优化：倍增很多时候是在查询过程中使用的（单次查询的时间复杂度通常为O（1）至 .在查询速度优化的同时，往往也需要对数据的预处理.

图论：在大多数情况下，图论中的点或边都可以按某种方式排序.如果问题的解要求O（NlogN）的时间复杂度，可以考虑倍增思想.在使用倍增思想的情况下，可以结合DP的"最优子结构"和ST表的思想尝试求解.

二进制：在许多情况下，倍增的具体实现与二进制运算有关.在使用倍增思想的过程中，往往可以结合二进制进行考虑.比如：尝试使用位运算优化状态转移.（如：（1<<i）在ST表和倍增求LCA中的应用和（i=i>>1，i&1）在快速幂中的应用）

加速DP状态转移：有时候可以使用倍增的方法优化DP（如：快速幂），使用这种方法可以参考快速幂的实现.

倍增与LCA

LCA最近公共祖先，相当于在树上找最短路，因为找到了最近公共祖先就相当于找到了最短路

找到u和v第一个不同祖先不同的位置，然后这个位置向上走一步就是最近公共的祖先

但是想找到u,v第一个不同祖先的位置，就要保证u,v在同一深度（才能一起往上移动）

所以这个过程分为三部分，预处理找到每个节点深度，把较深的一点移动到较浅一点的高度，两个一起往上移动直到他们的父亲相同

可以先用一个dfs找到所有节点的深度，用deep数组存下

vector<int>ve[100009];
void dfs(int u)
{
    for(int i=0;i<ve[u].size();i++)
    {
        int v=ve[u][i];
        if(vis[v]==0)
        {
            vis[v]=1;///标记
            deep[v]=deep[u]+1;
            dfs(v);
        }
    }
}

 

 

找到了深度怎么利用倍增往上移动呢

我们定义father[i][j]为i这个位置往上移动2^j次的祖先是谁

因为i移动2^j次就相当于从i移动2^(j-1)次后再移动2^(j-1)次 找到状态转移方程 father [ i ] [ j ] = father [ father [ i ] [ j -1] ] [ j-1 ] ;

然后利用dp做一个预处理

void st(int n)///倍增预处理i 节点上面1<<j步的节点
{
    for(int j=1; (1<<j)<=n; j++)
        for(int i=1; i<=n; i++)
            father[i][j]=father[father[i][j-1]][j-1];
}

 

输入边的时候就把father[i][0]初始化好，father[i][0]表示i节点上面2的0次方的祖先

 

 

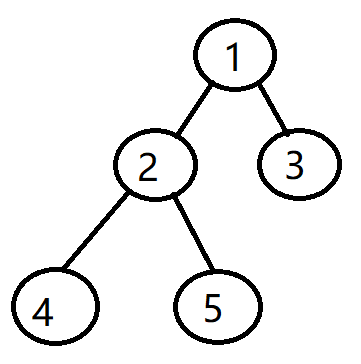
father[1][0]=0表示没有祖先，这个1节点就是根
father[2][0]=1表示2号节点祖先是1
以此内推father[4][0]=2 father[5][0]=2 father[3][0]=1
处理father[4][1]的时候就可以通过 father[ father[4][0]] [ 0 ]得到
father[4][0]=2 所以 father[4][1]=father[2][0]就意味着 i的上面2个节点可以通过i的上面1个节点的再跳1个节点得到 同理4个节点可以跳2次2个节点得到.

int LCA(int u,int v)
{
    if(deep[u]<deep[v])///默认u的深度大
        swap(u,v);
    int h=deep[u]-deep[v];///求出高度差
    for(int i=0; i<20; i++) ///这个操作可以将u节点向上提升任意高度
    {
        if(h&(1<<i))///二进制位上存在1就提升 1<<i步
        {
            u=father[u][i];
        }
    }
    if(u==v)///如果u==v表示 u就是v下面的分支节点
        return u;
    for(int i=19; i>=0; i--) ///找到第一个不相同的节点
    {
        if(father[u][i]!=father[v][i])
        {
            u=father[u][i];
            v=father[v][i];
        }
    }
    return father[u][0];///第一个不相同的节点的上一个就是最近公共祖先
}

 

通过这种方法，u和v一定能够到达这样一种状态——它们当前 不重合，如果再往上蹦一步，就会重合。所以再往上蹦一步得 到的就是LCA

 

附洛谷模板题代码：https://www.luogu.com.cn/problem/P3379

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(a) ((a) & -(a))
#define clean(a, b) memset(a, b, sizeof(a))
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const int maxn = 5e5 + 9;
const int Maxn = 29;


int deep[maxn],father[maxn][Maxn];
vector<int>ve[maxn];
int vis[maxn];
void dfs(int now)
{
    int len=ve[now].size();
    vis[now]=1;
    for(int i=0;i<len;i++)
    {
        int next=ve[now][i];
        if(!vis[next]) 
        {
            deep[next]=deep[now]+1;
            father[next][0]=now;
            dfs(next);
        }
    }
}
void st(int n)///倍增预处理i 节点上面1<<j步的节点
{
    for(int j=1; (1<<j)<=n; j++)
        for(int i=1; i<=n; i++)
            father[i][j]=father[father[i][j-1]][j-1];
}
int LCA(int u,int v)
{
    if(deep[u]<deep[v])///默认u的深度大
        swap(u,v);
    int h=deep[u]-deep[v];///求出高度差
    for(int i=0; i<20; i++) ///这个操作可以将u节点向上提升任意高度
    {
        if(h&(1<<i))///二进制位上存在1就提升 1<<i步
        {
            u=father[u][i];
        }
    }
    if(u==v)///如果u==v表示 u就是v下面的分支节点
        return u;
    for(int i=19; i>=0; i--) ///找到第一个不相同的节点
    {
        if(father[u][i]!=father[v][i])
        {
            u=father[u][i];
            v=father[v][i];
        }
    }
    return father[u][0];///第一个不相同的节点的上一个就是最近公共祖先
}
int main()
{
    int n,m,s,u,v,a,b;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&u,&v);
        ve[u].push_back(v);
        ve[v].push_back(u);
    }
    dfs(s);
    st(n);
    while(m--)
    {
        scanf("%d%d",&a,&b);
        printf("%d\n",LCA(a,b));
    }
    return 0;
}

 

倍增与RMQ

RMQ（Range Minimum/Maximum Query），即区间最值查询，是指这样一个问题：对于长度为n的数列A，回答若干询问RMQ（A,i,j）(i,j<=n)，返回数列A中下标在i，j之间的最小/大值

这样的问题我们可以用线段树来解决，但代码比较冗长，用ST算法也可以解决这个问题，该算法一般用较长的时间做预处理，待信息充足以后便可以用较少的时间回答每个查询

ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询

预处理

我们定义f[i, j]表示从第i个数起连续2^j个数中的最大值

f[i, j]表示从第i个数起连续2^j个数中的最大值

 

f[i][j]表示i开始的连续2^j 个点的最大值。

则f[i][0]表示i开始连续1个点的最大值即a[i];

f[i][1]表示i开始连续2个点的最大值即a[i]和a[i+1]的最大值;

f[i][2]表示i开始连续4个点的最大值即a[i]~a[i+3]中的最大值；

f[i][3]表示i开始连续8个点的最大值即a[i]~a[i+7]中的最大值;

 ......

f[i][logn]开始连续n个点的最大值即 a[i]~a[i+n-1];(i+n-1<=n)

我们把f[i，j]平均分成两段（因为f[i，j]一定是偶数个数字），从 i 到i + 2 ^ (j - 1) - 1为一段，i + 2 ^ (j - 1)到i + 2 ^ j - 1为一段(长度都为2 ^ (j - 1))

f[i，j]就是这两段各自最大值中的最大值

状态转移方程f[i, j]=max（f[i，j-1], f[i + 2^(j-1)，j-1]）

void ST(int n)///预处理
{
    for(int i=1;i<=n;i++)
        f[i][0]=a[i];///初始化
    for(int j=1;(1<<j)<=n;j++)///枚举区间长度
    {
        for(int i=1;i+(1<<j)-1<=n;i++)///枚举起点
        f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    }
}

 

查询

假如我们需要查询的区间为(i,j)，那么我们需要找到覆盖这个闭区间(左边界取i，右边界取j)的最小幂 （区间重复并不影响答案，因为我们要找的是最大或最小值）

因为这个区间的长度为j - i + 1,所以我们可以取k=log2( j - i + 1)，则有：RMQ(A, i, j)=max{f[i , k], f[ j - 2 ^ k + 1, k]}

 

int RMQ(int l,int r)
{
       int k=floor(log2( r-l+1 ));///向下取整
       printf("k=%d\n",k);
       return max(f[l][k],f[r-(1<<k)+1][k]);
}

 

整理自用，如有问题请尽快联系我 QQ：1661027159