文献翻译|Design of True Random Number Generator Based on Multi-stage Feedback Ring Oscillator(基于多级反馈环形振荡器的真随机数发生器设计)
基于多级反馈环形振荡器的真随机数发生器设计
摘要
真随机数生成器(trng)在加密系统中起着重要的作用。本文提出了一种在现场可编程门阵列(FPGA)上生成真随机数的新方法,该方法以 多级反馈环形振荡器(MSFRO) 的随机抖动为熵源。在传统环形振荡器的基础上,增加了多级反馈结构,扩大了时钟抖动的范围,提高了时钟采样频率和熵源的随机性。与传统的时钟采样结构不同,我们利用MSFRO产生的时钟抖动信号对FPGA的锁相环(PLL)产生的时钟信号进行采样。对得到的输出值进行异或运算,以减小输出值的偏差,提高其随机性。TRNG在Xilinx Virtex-6 FPGA中实现,硬件资源消耗低,吞吐量高。将熵源分类、硬件资源和吞吐量与现有trng进行了比较。结果表明,拟合成的TRNG只消耗24个lut和2个DFFs。与其他trng相比,该设计硬件资源消耗非常低,吞吐量可达290 Mbps。此TRNG生成的随机位序列通过NIST SP800-22测试和NIST SP80090B测试。
关键词:真随机数发生器、FPGA、多级反馈、频率积累
一、引入
真随机数发生器(TRNG)在许多密码系统中都扮演着重要的角色,包括密码生成、认证协议、密钥生成、随机填充和数字图像加密[1]、[2]。此外,真随机数在数值计算、统计模拟、随机抽样和量子密钥分配等方面也有重要的应用。
TRNG的性能指标包括吞吐量、硬件资源消耗和随机数统计。TRNG严格满足统计要求,具有不可预测性,利用随机物理过程作为熵源产生随机数。熵源包括热噪声、亚稳态[3]、时钟抖动[4]、混沌[5]和磁隧道结(MTJ)[6]、[7]、[8]。
如果原始随机比特流的随机性不好,则需要进行冯·诺伊曼校正或引入哈希函数等后处理操作来提高随机性。
基于FPGA设计的trng的熵源一般是环振荡器、DCM[9]、自定时环(STR)[4]以及触发[3]的设定时间和保持时间的违反所引起的亚稳定。
TRNGs利用RO电路中的时钟抖动作为熵源,在长时间抖动积累下可以获得良好的随机性,但吞吐量会降低,硬件资源消耗大。主要受RO阶数的影响,输出频率降低,导致吞吐量降低。提出的基于快速进位逻辑的TRNG可以提高吞吐量,但为了获得更严重的路径延迟,需要繁琐的布线以提高随机性。在采用锁相环或数字时钟管理器(DCM)作为熵源的trng中,熵源结构简单,但随机性较差,需要进行复杂的计算才能找到合适的参数[9]。
因此,为了提高trng的吞吐量,减少FPGA上的硬件资源消耗。在本文中,我们提出了一种可以提高熵源随机性的熵源结构。由该熵源组成的TRNG具有以下三个优点:熵源质量好。采用多级反馈结构可以在短时间内增加时钟的相位抖动,改善熵源的随机性。该方法的吞吐率高,且熵源产生的抖动信号频率高。我们使用抖动信号对传统时钟信号进行采样,随机比特流产生的速率就是抖动信号的频率。采样电路简单。并且可以进一步降低硬件资源的消耗。
为了证明该结构的这些优点,我们在几个Virtex-6和Spartan-6 fpga上实现了TRNG。本文的其余部分结构如下。在第二部分,我们介绍了时钟抖动的产生原理和相关的研究。在第三部分,我们从理论上介绍了我们提高时钟抖动随机性的出发点,然后系统地介绍了我们提出的TRNG。第四部分介绍并讨论了随机性检验。最后,在第五部分中得出结论。
二、相关研究
时域时钟抖动和频域相位噪声是噪声影响时钟信号的两种方式。理想情况下,频率为F的固定脉冲的持续时间应为T=1/F,间隔为T/2的跳变边缘。然而,这样的信号并不存在。
如图1a所示,由于电路的热噪声和干扰,信号周期的长度总是会发生一定程度的变化,导致下一个跳边到达时间的不确定性。因此,在时域上,时钟频率的变化表现为时钟抖动,在频域上表现为相位噪声。
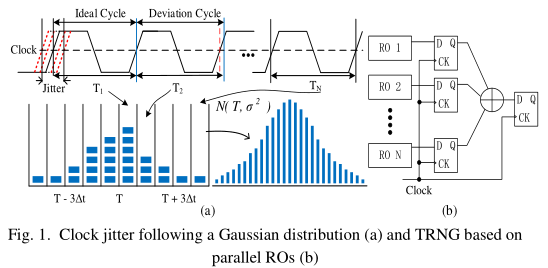
我们以时钟信号T1~TN的周期为样本,∆𝑡为时间间隔。我们对T1~TN样本进行统计分析。
如图1a所示,当∆𝑡趋于无穷大时,随机抖动的统计分布为𝑁(T,𝜎2)的高斯分布,其中T为理想边变化的时间点,𝜎2为抖动的方差。
利用时钟抖动产生随机数的基本原理是获得时钟信号上升沿或下降沿的不确定性。抖动定义为信号的定时事件与其期望位置之间的偏差。总抖动可分为随机抖动和确定性抖动。
随机抖动被认为是一种熵源,主要是由系统中的噪声或其他干扰引起的。如果我们对抖动范围内的数据进行采样,就可以得到一个随机数。
在基于FPGA的TRNG设计中,常用RO的时钟抖动作为熵源。然而,抖动范围很窄,难以提取。为了扩大抖动范围,RO需要长时间累积时钟抖动或增加阶数,但此时RO的频率会降低。
因此,基于RO设计的trng的吞吐量普遍较低。在[10]中,使用多个并行ROs生成随机比特流,如图1b所示。其目的是提高熵源的质量和吞吐量,但这将增加电路设计的复杂性,并消耗大量的硬件资源。我们可以在不增加电路复杂度的情况下,通过改进熵源结构来提高吞吐量,减少硬件资源的消耗。
三、多级反馈环形振荡器
在数字电路中,由于半导体噪声、温度变化、串扰和传播延迟,抖动会出现在RO时钟的上升沿或下降沿,并在RO中传播和累积。RO的周期大约是 𝑇=2𝑇𝑑elay*𝑁,这里的𝑇𝑑elay是一个逆变器(反相器)延迟,N是RO中逆变器(反相器)的数量。为了提高RO的频率,需要减少𝑇𝑑elay和逆变器(反相器)的数量𝑁。同时,为了改善RO的时钟抖动,需要增加逆变器的数量𝑁;这也将减少RO的频率。
在[11]中,提出了环形振荡器相位噪声与振荡器阶数的关系。它的表达式是:

其中𝐾为玻尔兹曼常数;𝑇为绝对温度;η,VDD, V, R, I为常数;𝑓0为RO的频率;𝑓为偏移频率;𝑝为环形振荡器的功耗;𝑁是环振子的阶数。当频率不固定时,增加𝑁会降低𝑓0频率,优化相位噪声,降低吞吐量。
频域相位噪声与时域平均抖动的关系为:
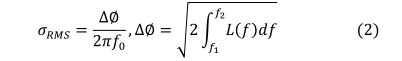
由式(2)可知,平均抖动与相位噪声正相关。此外,当信号频率𝑓0增大时,平均抖动𝜎𝑅MS变小,可以优化时钟抖动。因此,熵源的随机性变得更差。
为了解决这种矛盾,我们在RO电路中增加了多级反馈结构,反馈结构为单逆变器,这相当于增加RO的顺序。我
们的目的是将每个反馈结构和部分反激电路逆变器结合起来,形成一个可以独立工作的新的反激电路,使整个电路可以连续振荡。反馈结构增加了相位噪声,从而改善了熵源的随机性。
如图2所示,所提出的MSFRO是一个多级反馈结构。反馈结构的数量是奇数,因为当反馈结构成对出现时,由于耦合,它们会高度相关,这将大大降低TRNG[12]输出比特流的随机性。
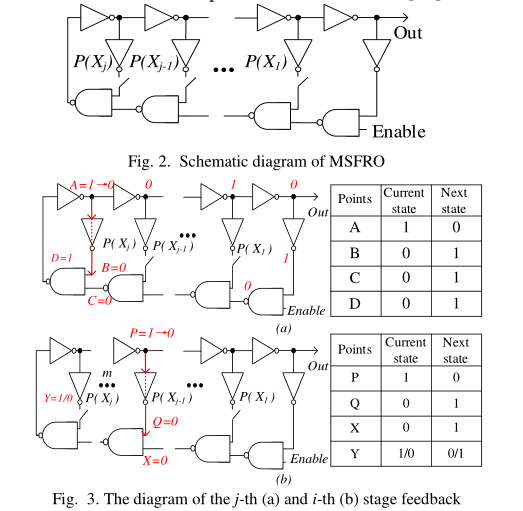
如图3a所示,在反馈的第j阶段,当A=1,B=0是通过反馈部分的逆变器得到的。C是从前一个顺序传播的值。然后用NAND运算B和C=0,得到D=1。D通过逆变器后,A的值从1变为0,形成振荡环,振荡周期缩短。
同样,当A=0时也可以形成振荡环。如图3b所示,在反馈的第i阶段,当A=1时,反馈后得到B=0。然后通过NAND运算B和C=0得到一个值。在通过m个逆变器后,这个值产生D=1/0,其中m = j-i+1。D通过m个逆变器后,值从1变为0。通过电路的反馈部分,可以有效地缩短振荡周期,提高振荡频率。
在本文中,我们提出了一种使该结构的频率高于传统RO的方法。这种方法叫做频率累积。首先,对方波进行傅里叶变换,得到:
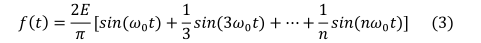
E是方波的振幅。通过在RO环中引入多个反馈阶段,可以在内部构建一个新的RO。每一个新的RO同时输出一个方波,这些方波累积形成一个新的方波。我们假设每个方波的傅里叶变换是扩大𝑓1(𝑡),𝑓2(𝑡),…,𝑓𝑗(𝑡)。对这些方波展开求和,得到如下表达式:
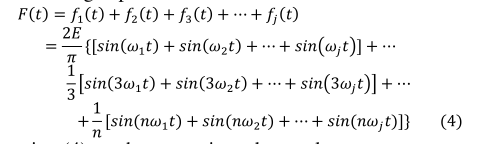
式(4)可近似等于:
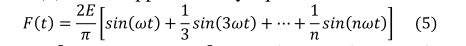
其中𝜔=[𝜔1,𝜔2,𝜔3,…,𝜔𝑗]。由此可见,式(5)应为方波。此外,频率的平方为: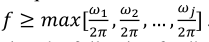 ,MSFRO结构使用以下反馈多项式定义:
,MSFRO结构使用以下反馈多项式定义:
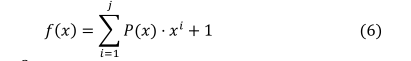
其中𝑗=(n−3)/2,𝑠>3且𝑠=2𝑘+1,𝑘>1且𝑘∈𝑁*。j为反馈部分逆变器个数,n为传统RO中逆变器个数,P(x)为反馈多项式系数且为常数表达式,即P(x)=1或P(x)=0。P(x)=1表示环路中有反馈连接,P(x)=0表示环路中没有反馈连接。如果反馈多项式P(x)的所有系数都为0,则反馈多项式为f(x)=1,表明回路中没有反馈。
我们用四种不同的模式对九阶MSFRO进行了实验。公式分别是f(x)=x+1, f(x)=x^2+1, f(x)=x^3+1, f(x)=x^3 +x^2+x+1。如图4所示,我们的TRNG结构使用两个msfro作为抖动信号源。
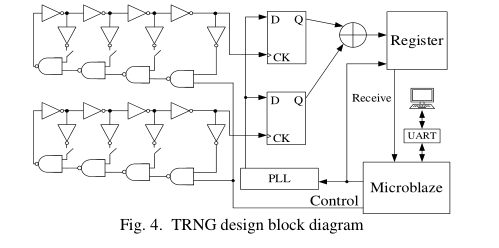
锁相环产生两个正常时钟。锁相环的输出作为触发器的数据输入,MSFRO的输出作为触发器的时钟信号输入。每次上升边缘的MSFRO输出信号来了,D触发器将采样锁相环输出信号产生一个随机比特。噪声引起的相位抖动范围很小,使用触发器采样时会采样很多确定的值,降低了随机数的随机性。因此,本文提出的TRNG采用两个MSFRO作为熵源,提取其随机性后直接通过异或输出得到随机数。
四、实验结果
A.NIST SP 800-22测试
本次试验验证了所提出的TRNG在标准操作条件(25℃,1.0V)下产生的序列的随机性。为了保证实验数据的准确性,避免单个开发板实验数据的偶然性,实验是在三个不同的Virtex-6 fpga开发板上进行的。
在不同的工作条件下,连续生成100万比特来测试随机性。Prop是十项测试的随机通过率。测试结果如表I所示,随机比特流可以通过每个高p值的随机测试。p值偏低可能是由于设备差异和单板布局的影响。但都通过了测试,说明TRNG可以生成真随机数。

B.NIST SP 800-90B测试
NIST SP800-90B测试比现有的熵估计方法更加复杂和严格。表II给出了IID检验、卡方检验和最长重复子串长度检验(LRS检验)的结果。实验结果表明,TRNG生成的比特流序列的最小熵为0.985281,通过了NIST SP800-90B测试中的IID测试。
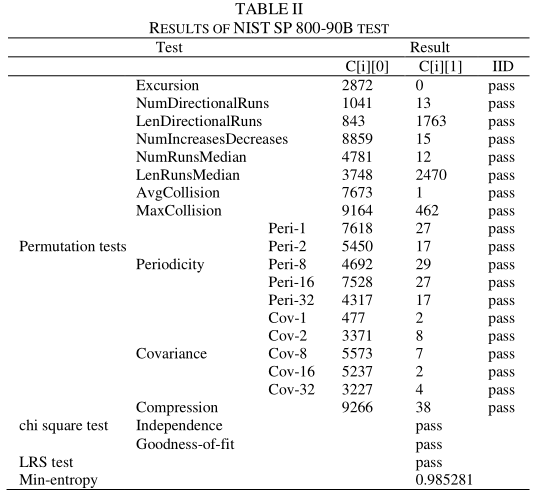
C.NIST测试结果在四种不同的模式
为了进一步验证结构的可靠性和合理性,我们对四种模态进行了试验。生成的随机比特流通过NIST SP800-22和SP800-90B进行测试。
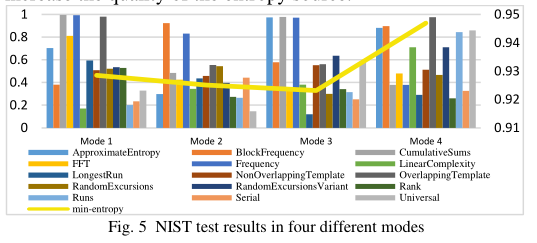
如图5所示,所有的位流都通过了NIST SP800-22测试,表明它们是真正的随机数。所有数据均通过NIST SP800-90B重新检验,以进一步确定所获得随机数的熵源质量。
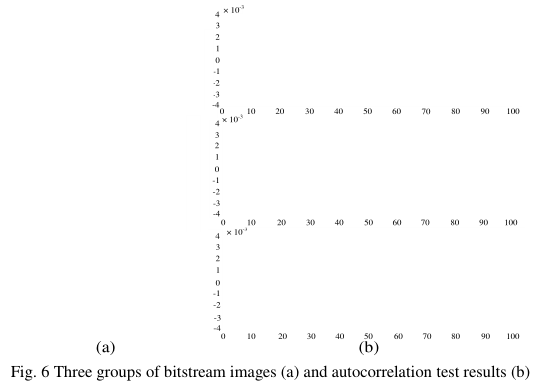
图6折线表示四种模式的最小熵值。模态4的最小熵为0.946909,高于其他三种模态。这是因为模式4有三种反馈结构,这会显著增加电路中的相位噪声,增加熵源的质量。
D.偏差检验和自相关检验
图6a显示了由三组100万连续位元生成的图像。我们可以清楚地看到,在本研究生成的图像中,黑白像素的分布非常均匀,因此生成的数据没有偏移,随机性好。检验随机序列的自相关就是检验序列的随机性。相关程度用相关系数表示。根据Karl Pearson设计的统计指标,相关系数小于0.3,可以认为相关不相关。
图6b为模式4结构测量的三组数据的自相关检验结果。从图中可以看出,各组数据的相关系数都在0.3以下。因此,所提出的TRNG生成的随机序列不具有自相关。
E.重启测试
在重新启动测试[13]中,我们绘制了6个重新启动测试的前几个采样位的数据。如图7所示,如果随机序列显示不同的图,则得到的数据为真正的随机序列。实验结果表明,每个测试产生了不同的随机序列。因此,本文设计的TRNG产生的随机序列不具有可重复性和相似性,是一个真正的随机序列。
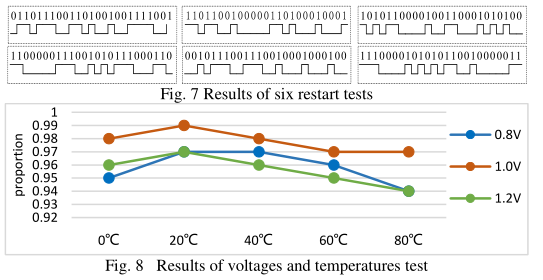
F.电压和温度测试
我们在Xilinx Virtex-6 FPGA上评估了TRNG在不同电压和温度下的性能。在不同的环境(温度0℃~80℃)和电压(0.8 V~1.2V)下进行了一些实验。如图8所示,在不同的温度和电压下进行了100组实验,每组实验采集了100万比特的比特流数据。对每一组测量数据进行NIST测试,以确定通过测试的百分比。由图8可以看出,在1.0V、20℃条件下,通过率最好,随机性最好。电压变化时,通过率减小,随机性减小。随着温度从20℃开始升高,通过率逐渐降低,随机性逐渐变差。
G.与其他基于FPGA的TRNG比较
我们将模式4的实验结果与其他trng进行比较,结果如表III所示。
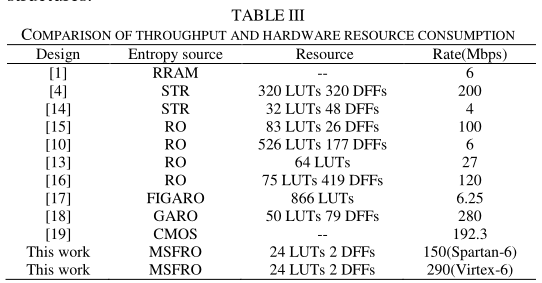
[1]的结构采用RRAM作为熵源,吞吐量低,只有6mbps。
[14]的结构采用STR作为熵源,吞吐量低,仅为4mbps。
[4]中,该结构采用STR作为熵源并行采样多个DFFs,吞吐量高达200mbps,但硬件资源消耗严重。这对于资源非常有限的FPGA来说非常不利。
[15],[10],[16]和[14]中的结构都使用RO作为熵源。
[15]和[16]的吞吐量分别为100 Mbps和120 Mbps,显著高于[10]和[13],但低于我们建议的TRNG (150 Mbps)。而且[15]和[16]的硬件资源消耗非常大。
[13]中的TRNG硬件资源消耗低,吞吐量低。
[10]中的TRNG不仅消耗大量硬件资源,而且吞吐量低。
[17]的结构采用FIGARO作为熵源,吞吐量低,只有6.25 Mbps。
[18]结构采用GARO作为熵源,吞吐量为280mbps。
[19]结构采用CMOS作为熵源,吞吐量为192.3 Mbps,但低于我们提出的TRNG (290mbps)。
总体而言,与其他架构相比,本文提出的TRNG具有更少的硬件资源消耗和更高的吞吐量。我们设置外部周期信号的频率范围为285~295MHz,用于注入锁定测试。共测试10组随机比特流数据,随机通过率为70%。
此外,我们在ISE中使用Xilinx XPower Analyzer来分析四种模式的功耗。如表4所示,由于存在多个反馈结构,模式4的功耗相对较高。

五、结论
我们利用本文提出的MSFRO时钟抖动来产生随机性。与现有的TRNG相比,我们的TRNG可以获得更高的吞吐量和更低的硬件资源开销,而且不需要复杂的提取结构。实验分析表明,所设计的TRNG性能良好,均通过了随机性测试。
提出的TRNG在spartan6 FPGA上的吞吐量为150 Mbps,在Virtex-6 FPGA上的吞吐量为290 Mbps,硬件资源开销仅为24个lut和2个DFFs。因此,我们节省了大量的硬件资源,并提供了更紧凑的TRNG设计。
REFERENCES
[1] R. Govindaraj, S. Ghosh and S. Katkoori, "CSRO-Based Reconfigurable True Random Number Generator Using RRAM," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 26, no. 12, pp. 2661-2670, Dec. 2018, doi: 10.1109/TVLSI.2018.2823274.
[2] P. Poudel, B. Ray and A. Milenkovic, "Microcontroller TRNGs Using Perturbed States of NOR Flash Memory Cells," in IEEE Transactions on Computers, vol. 68, no. 2, pp. 307-313, 1 Feb. 2019, doi: 10.1109/TC.2018.2866459.
[3] P. Z. Wieczorek and K. Gołofit, "Dual-Metastability Time-Competitive True Random Number Generator," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 61, no. 1, pp. 134-145, Jan. 2014, doi: 10.1109/TCSI.2013.2265952.
[4] Cherkaoui A et al., “A Very High Speed True Random Number Generator with Entropy Assessment”. In Cryptographic Hardware and Embedded Systems - CHES 2013, vol. 8086. pp179-196, Aug.2013, Doi: 10.1007/978-3-642-40349-1_11.
[5]Y Hosokawa and Y Nishio, "Simple chaotic circuit using cmos ring oscillators," Internalional Journal of Bijllrcalion and Chaos, vol. 14, no. 07, pp. 2513-2524, 2004
[6] E. I. Vatajelu and G. Di Natale, "High-Entropy STT-MTJ-Based TRNG," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 27, no. 2, pp. 491-495, Feb. 2019, doi: 10.1109/TVLSI.2018.2879439.
[7] A. Amirany, K. Jafari and M. H. Moaiyeri, "True Random Number Generator for Reliable Hardware Security Modules Based on a Neuromorphic Variation-Tolerant Spintronic Structure," in IEEE Transactions on Nanotechnology, vol. 19, pp. 784-791, 2020, doi: 10.1109/TNANO.2020.3034818.
[8] I. Alibeigi, A. Amirany, R. Rajaei, M. Tabandeh, and S. B. Shouraki, "A Low-Cost Highly Reliable Spintronic True Random Number Generator Circuit for Secure Cryptography," Spin, vol. 10, no. 01, 2019, doi: 10.1142/s2010324720500034.
[9] N. Fujieda, M. Takeda and S. Ichikawa, "An Analysis of DCM-Based True Random Number Generator," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 6, pp. 1109-1113, June 2020, doi: 10.1109/TCSII.2019.2926555.
[10] N. Nalla Anandakumar, S. K. Sanadhya and M. S. Hashmi, "FPGA-Based True Random Number Generation Using Programmable Delays in Oscillator-Rings," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 3, pp. 570-574, March 2020, doi: 10.1109/TCSII.2019.2919891.
[11] A. Hajimiri, S. Limotyrakis and T. H. Lee, "Jitter and phase noise in ring oscillators," in IEEE Journal of Solid-State Circuits, vol. 34, no. 6, pp. 790-804, June 1999, doi: 10.1109/4.766813.
[12] K. Wold and S. Petrović, "Security properties of oscillator rings in true random number generators," 2012 IEEE 15th International Symposium on Design and Diagnostics of Electronic Circuits & Systems (DDECS), 2012, pp. 145-150, doi: 10.1109/DDECS.2012.6219041.
[13] Sivaraman R, Rajagopalan, S. & Amirtharajan, “FPGA based generic RO TRNG architecture for image confusion,” Multimed Tools Appl, vol 79, pp 13841–13868, Feb 2020, doi: 10.1007/s11042-019-08592-z.
[14] H. Martin, P. Peris-Lopez, J. E. Tapiador and E. San Millan, "A New TRNG Based on Coherent Sampling With Self-Timed Rings," in IEEE Transactions on Industrial Informatics, vol. 12, no. 1, pp. 91-100, Feb. 2016, doi: 10.1109/TII.2015.2502183.
[15] K. Wold and C. H. Tan, "Analysis and Enhancement of Random Number Generator in FPGA Based on Oscillator Rings," 2008 International Conference on Reconfigurable Computing and FPGAs, 2008, pp. 385-390, doi: 10.1109/ReConFig.2008.17.
[16] Wang Y, Hui C, Liu C, Xu C. Theory and implementation of a very high throughput true random number generator in field programmable gate array. Rev Sci Instrum. 2016;87(4):044704. doi:10.1063/1.4945564.
[17] K. Demir and S. Ergun, "Random Number Generators Based on Irregular Sampling and Fibonacci–Galois Ring Oscillators," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 66, no. 10, pp. 1718-1722, Oct. 2019, doi: 10.1109/TCSII.2019.2933280.
[18] J. Lin, Y. Wang, Z. Zhao, C. Hui and Z. Song, "A New Method of True Random Number Generation based on Galois Ring Oscillator with Event Sampling Architecture in FPGA," 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), 2020, pp. 1-6, doi: 10.1109/I2MTC43012.2020.9129357.
[19] S. Larimian, M. R. Mahmoodi and D. B. Strukov, "Lightweight Integrated Design of PUF and TRNG Security Primitives Based on eFlash Memory in 55-nm CMOS," in IEEE Transactions on Electron Devices, vol. 67, no. 4, pp. 1586-1592, April 2020, doi: 10.1109/TED.2020.2976632.
本文来自博客园,作者:shihao_Yang,转载请注明原文链接:https://www.cnblogs.com/Yang-shihao/p/15483776.html

