求最大公约数的三种方法解析

 

求最大公约数的三种方法解析

指两个或多个整数共有约数中最大的一个。

最小公倍数:它与最大公约数的乘机为所求数之积。

比如求 x,y的最大公约数和最小公倍数

记住这个公式： x * y=最小公倍数 * 最大公约数

 1.辗转相除法

 

 

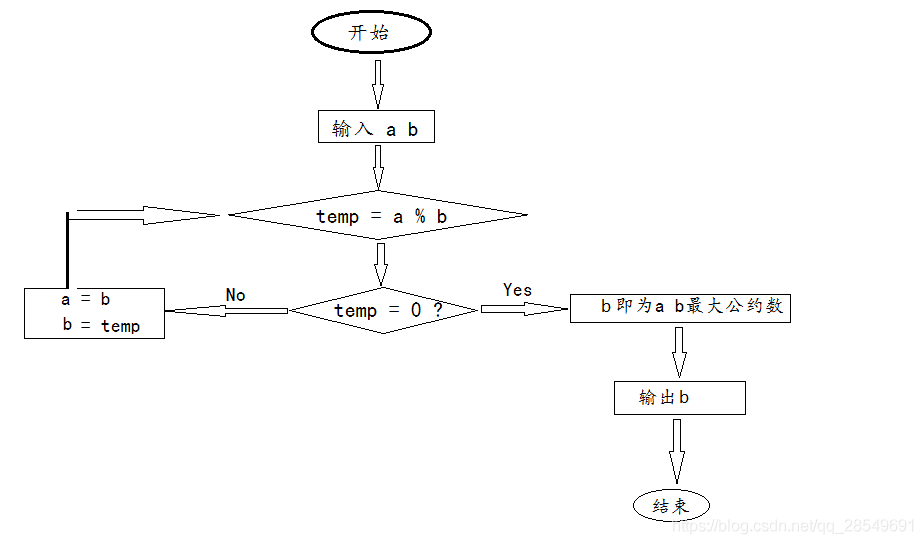
int gcd(int a, int b)
    {
        if (a % b == 0)
            return b;
        else
            return gcd(b, a % b);
    }

 

或

int gcd(int a, int b)
{
    int temp;
    while (a % b)
    {
        temp = b;
        b = a % b;
        a = temp;
    }
    return b;
}

2.辗转相减法

int gcd(int a, int b)
{
    while (a != b) //若a = b，则a（或b）即为两数的最大公约数
    {
        if (a > b)
            a = a - b;
        else
            b = b - a;
    }
    return a;
}

3.穷举法

int gcd(int a, int b)
{
    int  tmp;
    tmp = (a > b) ? b : a;
    while (tmp > 0)
    {
        if (a % tmp == 0 && b % tmp == 0)//只要找到一个能同时被a,b所整除的数，则中止循环
            break;
        --tmp;
    }
    return tmp;
}

int lcm(int u, int v) //求最小公倍数
{
    int tmp = gcd(u, v);
    return u * v / tmp;
}