树及其常用方法

树

定义

树是一种特殊的数据结构，他可以用来描述有分支的结构，是有一个或一个以上的节点所组成的优先集合

一些关键名词

• 树根或根节点(root)： 没有父节点的节点为根节点

• 父节点(parent): 每一个节点的上层节点为父节点

• 子节点(children): 每一个节点的下层节点为子节点

• 兄弟节点(slblings):有共同父节点的节点为兄弟节点

• 度(degree): 子数的个数为该节点的度

• 终端节点或叶子节点(terminal node):没有子节点的节点，即度为0的节点

• 非终端节点(non-terminal node):叶子意外的节点均为非终端节点，即度不为0的节点

• 阶层或级(level)：数的层级

• 高度(height): 数的最大阶度

• 树林(forest):树林是由n个互斥树的集合，移去树根即为树林

• 祖先(ancestor)和子孙(descendent):所谓祖先，是指从树根到该节点路径上锁包含的节点，而子孙则是在该节点字数中的任意节点

特质

1. 存在一个特殊的节点称为树根(root)

2. 其余的节点分为n => 0 个互斥的集合,T1, T2, T3且每个集合称为子树

二叉树

遵守小于父节点的值放在左子节点，大于父节点的值放在右子节点

二叉树的遍历

• 中序遍历：左子树->树根->右子树

• 前序遍历：树根->左子树->右子树

• 后序遍历：左子树->右子树->树根

 

链表实现二叉树

TreeNode

 package 链表实现;
 ​
 /**
  * @author YanAemons
  * @date 2021/10/11 16:05
  */
 public class TreeNode {
     int value;
     TreeNode left_Node;
     TreeNode right_Node;
 ​
     public TreeNode(int value)
     {
         this.value = value;
         this.left_Node = null;
         this.right_Node = null;
     }
 }
 ​

BinaryTree

 package 链表实现;
 ​
 import sun.reflect.generics.tree.Tree;
 ​
 /**
  * @author YanAemons
  * @date 2021/10/11 16:06
  */
 public class BinaryTree {
     public TreeNode rootNode;
     public BinaryTree(int[] data)
     {
         for (int i = 0; i < data.length; i++)
         {
             Add_Node_To_Tree(data[i]);
         }
     }
 ​
     void Add_Node_To_Tree(int value)
     {
         TreeNode currentNode = rootNode;
         if (rootNode == null)
         {
             rootNode = new TreeNode(value);
             return;
         }
 ​
         while(true)
         {
             if (value < currentNode.value)
             {
                 if (currentNode.left_Node == null)
                 {
                     currentNode.left_Node = new TreeNode(value);
                     return;
                 }
                 else currentNode = currentNode.left_Node;
             }
             else {
                 if (currentNode.right_Node == null)
                 {
                     currentNode.right_Node = new TreeNode(value);
                     return;
                 }
                 else currentNode = currentNode.right_Node;
             }
         }
     }
 ​
 }
 ​

Main

 package 链表实现;
 ​
 import java.io.BufferedReader;
 import java.io.IOException;
 import java.io.InputStreamReader;
 ​
 /**
  * @author YanAemons
  * @date 2021/10/11 16:11
  */
 public class Main {
     public static void main(String[] args) throws IOException {
         int ArraySize = 10;
         int tempdata;
         int[] content = new int[ArraySize];
         BufferedReader keyin = new BufferedReader(new InputStreamReader(System.in));
         System.out.println("请输入连续"+ArraySize+"个数据");
         for (int i = 0; i < ArraySize; i++)
         {
             System.out.print("请输入第"+(i+1)+"个数据");
             tempdata = Integer.parseInt(keyin.readLine());
             content[i] = tempdata;
         }
         new BinaryTree(content);
         System.out.println("===以链表方式建立二叉树,成功!!===");
     }
 }
 ​

二叉运算树

1. 考虑算术式中运算符的结合性与优先权，在适当的加上括号

2. 在由最内层的括号逐步向外，利用运算符当树根，左边操作数当左子树，右边操作数当右子树，其中优先权最低的运算符作为此儿茶运算树的树根

二叉排序树

1. 第一个输入数据当作此二叉树的树根

2. 之后的数据以递归的方式与树根进行比较，小于树根置于左子树，大于树根置于右子树

二叉搜索树的特点

1. 可以是空集合，但若不是空集合则节点上一定要有一个键值

2. 每一个树根的值需大于左子树的值每一个树根的值需小于右子树的值

3. 左右子树也是二叉搜索数

4. 树的每一个节点值都不相同

线索二叉树(Threaded Binary Tree)

就是把这些空的连接加以利用，再指到数的其他节点，而这些连接就称为"线索",而这颗树就称为线索二叉树

将二叉树转换为线索二叉树的步骤如下:

1. 先将二叉树通过中序遍历方式按序排，并将所有空链接改成线索

2. 如果线索链接指向该节点的左连接，则将该线索指到中序遍历顺序下前一个节点

3. 如果线索指向该节点的右链接，则将该线索指到中序遍历顺序下的后一个节点

4. 指向一个空节点，并将此空节点的右链接指向自己，而空节点的左子树是此线索二叉树

基本结构: LBIT--LCHILD--DATA--RCHILD--RBIT

• LBIT:左控制位

• LCHILD：左子树链接

• DATA:节点数据

• RCHILD：右子树链接

• RBIT：右控制位

树的二叉树表示法

1. 将节点的所有兄弟节点，用平行线连接起来

2. 删掉所有与子节点的连接，只保留与最左子节点的连接

3. 顺时针旋转45°

   

    

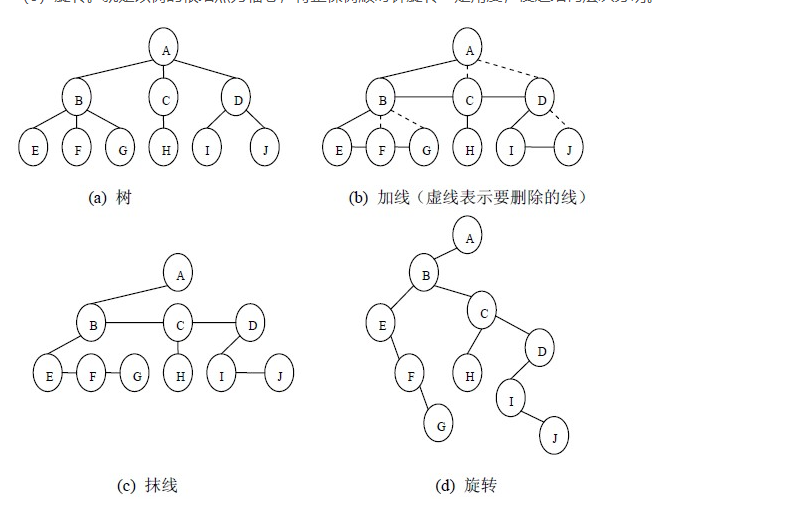
树林转换为二叉树

1. 由左至右将没课树的树根连接起来

2. 仍然利用树转换为二叉树的方法操作