查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 陈泽役 |
0.PTA得分截图

1.本周学习总结
1.1 查找的性能指标
ASL(Average Search Length),即平均查找长度,在查找运算中,由于所费时间在关键字的比较上,所以把平均需要和待查找值比较的关键字次数称为平均查找长度。
定义:ASL=∑ni=1pici。
ASL的计算与移动次数和比较次数有关,决定了该查找算法的时间复杂度。
1.2 静态查找
- 顺序查找
从表的一端开始,逐个扫描,将扫描到的关键字和给定的k值比较,若相等则查找成功,若扫描结束后,未找到关键字的记录,则查找失败。
int SeqSearch(int *a,int n,int k)
{
int i=0;
while(i<n&&a[i]!=k)
{
i++;
}
if(i>=n) //没找到,返回-1
{
return -1;
}
else
{
return i;
}
}
时间复杂度:O(n)
- 二分查找
设n个元素的数组a已经有序,用low和high两个变量来表示查找的区间,即在a[low]~a[high]中去查找用户输入的值x,和区间中间位置的元素a[mid] (mid=(low+high)/2)作比较,如果相等则找到,算法结束;如果是大于则修改区间(数组为升序数列:low=mid+1;数组为降序数列:high=mid-1);如果是小于也修改区间(数组为升序的改为:high=mid-1,;数组为降序数列:low=mid+1);一直到x=a[mid] (找到该值在数组中的位置)或者是low>high(在数组中找不到x的值)时算法终止;
int BinSearch(int *a,int n,int k)
{
int low=0,high=n-1,mid;
while(low<=high)
{
mid=(mid+high)/2;
if(a[mid]==k)
{
return mid+1;
}
if(k<a[mid])
{
high=mid-1;
}
else
{
low=mid+1;
}
}
return -1; //没找到
}
//递归代码
int BinSearch(int *a,int low,int high,int k)
{
int mid;
if(low<high)
{
mid=(low+high)/2;
if(a[mid]==k)
return mid+1;
if(a[mid]>k)
BinSearch(a, low,mid-1, k) ;
else
BinSearch(a, low,mid+1, k) ;
}
else
return -1;
}
时间复杂度:O(logn)
1.3 二叉搜索树
二叉排序树要么是空二叉树,要么具有如下特点:
- 二叉排序树中,如果其根结点有左子树,那么左子树上所有结点的值都小于根结点的值;
- 二叉排序树中,如果其根结点有右子树,那么右子树上所有结点的值都大小根结点的值;
- 二叉排序树的左右子树也要求都是二叉排序树;
1.3.1 如何构建二叉搜索树(操作)
- 插入

插入关键字k结点要保证插入后仍然满足BST的性质。
插入过程为:
1.若二叉排序树为空,则在给定的一系列关键字序列中,将第一个关键字设为根节点。
2.若不为空,则与根节点的关键字作比较
若比根节点小,作为该根节点的左子树;
若比根节点大,作为该根节点的右子树;
若相等,则无需插入。
- 删除
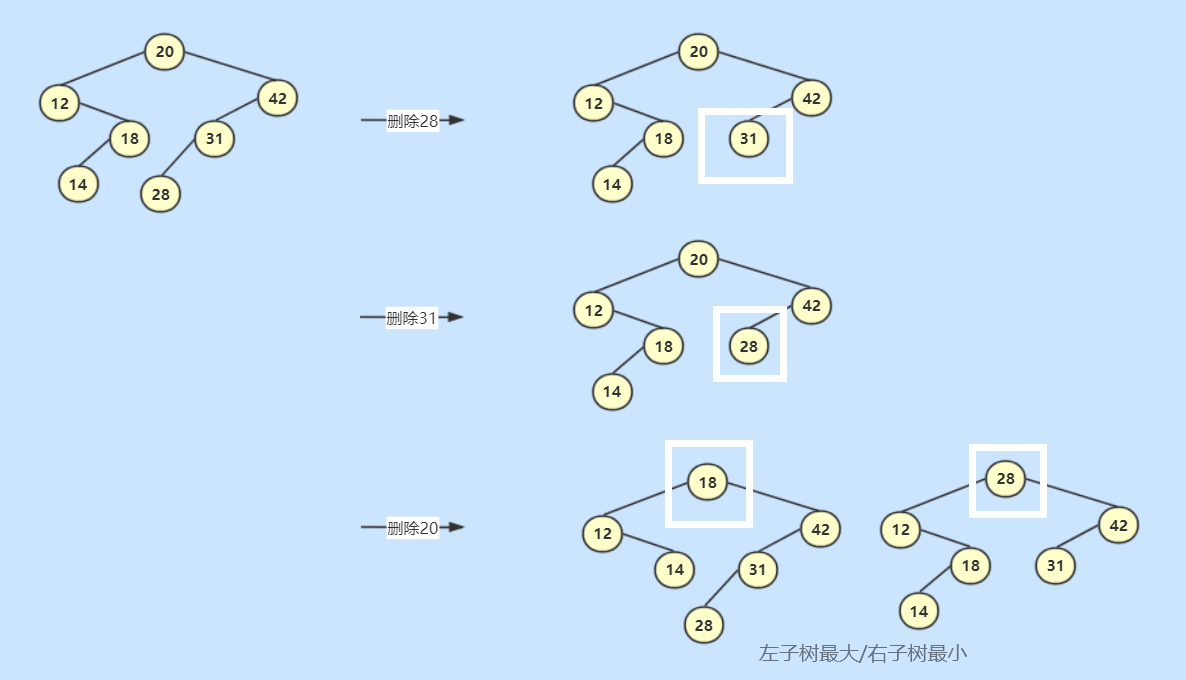
在删除操作前先用要找到待删除节点的位置
删除二叉树的结点又有三种情况:
1.删除叶子节点,可以直接删除,也就是直接让他的双亲结点为空
2.删除带有一个子节点的节点,则让不为空的子树取代被删结点,也就是让它的双亲结点指向它的不空子树
3.删除带有两个子节点的结点,可用它的前驱结点(左子树中最大的数,即左子树的最右结点)取代它,或是用它的后继节点(右子树中最小的节点,即右子树中最左的节点)取代它
1.3.2 如何构建二叉搜索树(代码)
- 结构体定义
typedef int KeyType; //关键字类型
typedef char* InfoType; //其他数据类型
typedef struct node
{
KeyType key; //关键字域
InfoType data; //其他数据域
struct node *lchild, *rchild;/*左右孩子*/
}BSTNode, * BSTree;
- 构建
void CreateBST(BinTree& BST, int n)/*建树函数*/
{
int x;
BST = NULL;//树初始化为空
for (int i = 0; i < n; i++)
{
cin >> x;
Insert(BST, x);
}
}
- 插入
void Insert(BinTree& BST, int X)
{
if (BST == NULL)/*树空*/
{
BST = new TNode;/*申请*/
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else if (X > BST->Data)/*大于插左边*/
{
Insert(BST->Left, X);
}
else if (X < BST->Data)/*小于插右边*/
{
Insert(BST->Right, X);
}
}
- 查找
BinTree Find(BinTree BST, ElementType X)
{
if (BST == NULL)
{
return NULL;/*为空返回空*/
}
if (X > BST->Data)
{
Find(BST->Right, X);/*大于在右*/
}
else if (X < BST->Data)
{
Find(BST->Left, X);/*小于在左*/
}
else
{
return BST;/*找到则返回*/
}
}
1.4 AVL树
- AVL树解决什么问题,其特点是什么?
结合一组数组,介绍AVL树的4种调整做法。
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
1.LL
LL情况需要右旋解决,如下图所示:
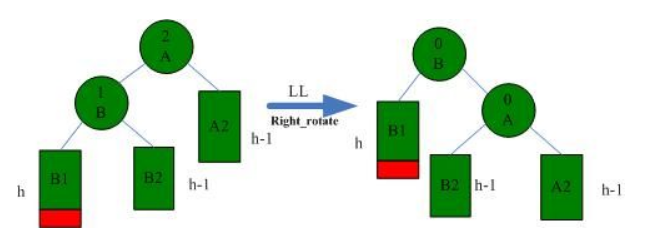
2.RR
RR情况需要左旋解决,如下图所示:
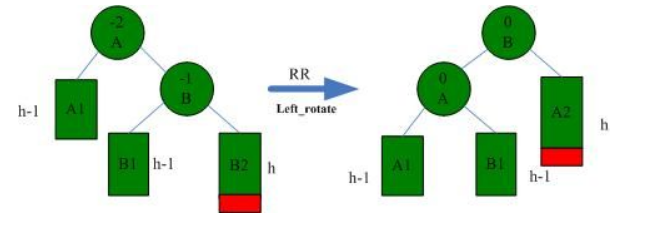
3.LR
LR情况需要左右(先B左旋转,后A右旋转)旋解决,如下图所示:
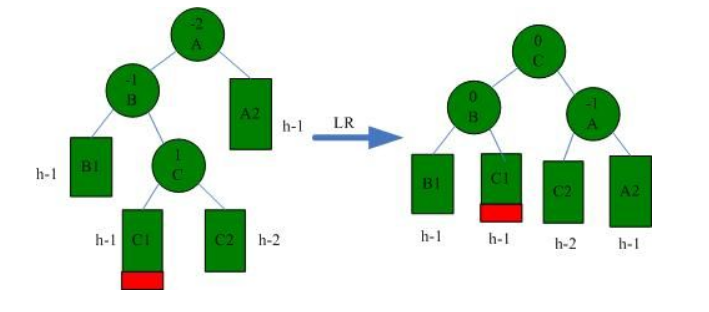
4.RL
RL情况需要右左旋解决(先B右旋转,后A左旋转),如下图所示:
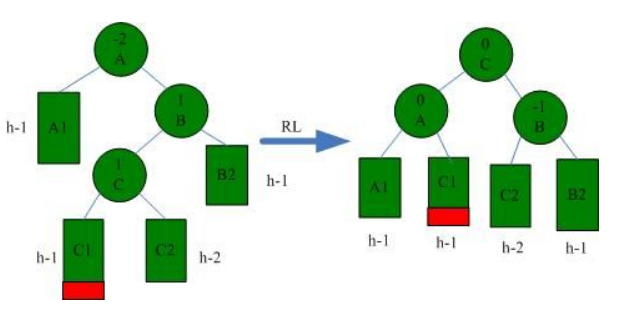
1.5 B-树和B+树
B-树
-
定义:是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2; 2.根结点的儿子数为[2, M]; 3.除根结点以外的非叶子结点的儿子数为[M/2, M]; 4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字) 5.非叶子结点的关键字个数=指向儿子的指针个数-1; 6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1]; 7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树; 8.所有叶子结点位于同一层; -
B-树的特性:
1.关键字集合分布在整颗树中;2.任何一个关键字出现且只出现在一个结点中; 3.搜索有可能在非叶子结点结束; 4.其搜索性能等价于在关键字全集内做一次二分查找; 5.自动层次控制;
B+树
-
定义:B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了: 2.非叶子结点的子树指针与关键字个数相同; 3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间); 5.为所有叶子结点增加一个链指针; 6.所有关键字都在叶子结点出现; -
B+树的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;2.不可能在非叶子结点命中; 3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层; 4.更适合文件索引系统;
1.6 散列查找
哈希表(又称散列表),是一种存储结构,适用于记录的关键字与存储的地址存在某种关系的数据。设要存储的元素个数为n,再设计长度为m的连续内存单元,通过改变下标改变对应的映射关系,元素存储在内存单元中。
哈希表的设计:主要是为了解决哈希冲突。在实际应用中,哈希冲突是难以避免的,而它主要与三个因素有关。
哈希函数的构造方法可采用直接定址法和除留余数法,除留余数法中h(k)=k mod p,p取不大于m的素数时效果最好,减少发生冲突的可能。

