超级变变变
Description
经过一系列的游戏之后,你终于迎来了今天的作业,第一个作业是预习一个超级美好的函数f(x),描述如下。
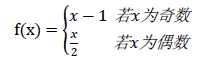
为了研究这个函数的性质,你决定定义一次变化为x=f(x)。
若x就经过若干次变化为k,则你就会觉得这是一个k变变数。
现在既然你已经这么觉得了,那就只好给定A,B,求有多少个A<=x<=B是k变变数了。
Input
输入包含三行。
第一行为一个整数k。
第二行为一个整数A。
第三行为一个整数B。
Output
输出仅一行,表示答案。
Sample Input
Sample Input 1
13
12345
67890123
Sample Input2
1
234567
1234567
Sample Output
Sample Output1
8387584
Sample Output2
1000001
Data Constraint
Hint
对于50%的数据,0<=k,A,B<=10^6
对于100%的数据,0<=k,A,B<=10^18 A<=B
.
.
.
.
.
分析
对于一个k,我们可以知道,它可以是由2 * k和2 * k+1变化得来的
而2 * k又是由2 * 2*k和2 * 2 * k+1变化得来的
同时2 * k+1又是由2 * (2 * k+1)和2 * (2 * k+1)+1变化得来的
以此类推,我们就可以得到一棵二叉树
其中,每一层的数字都是连续的,树上的每一个数字都可以通过变化得出k
利用这个性质,我们可以通过判断每一层有多少个数字在a~b的范围内从而逐层累加的出答案
然而,当k为偶数时
k不仅能由2 * k和2 * k+1变化得来,同时也能由k+1变化得来
因此,当k为偶数时,答案的统计也应该加上k+1的答案
由于任何数都可以变化得到0、1、2
所以,当k=0或1或2时,可以直接输出答案
要注意k有可能大于a
所以答案的统计范围为max(a,k)~b
.
.
.
.
.
.
程序:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int main()
{
long long k,a,b;
scanf("%lld",&k);
scanf("%lld",&a);
scanf("%lld",&b);
a=max(k,a);
if (k==0||k==1||k==2)
{
printf("%lld",b-a+1);
return 0;
}
long long ans=0,ta=k,tb=k;
while (ta<=b)
{
if (ta>=a)
{
if (tb<=b) ans+=tb-ta+1;
if (tb>b) ans+=b-ta+1;
}
if (ta<a)
{
if (tb>b)
{
ans+=b-a+1;
break;
}
}
ta=(long long)ta*2;
tb=(long long)tb*2+1;
}
if (k%2==0)
{
k++;
long long ta=k,tb=k;
while (ta<=b)
{
if (ta>=a)
{
if (tb<=b) ans+=tb-ta+1;
if (tb>b) ans+=b-ta+1;
}
if (ta<a)
{
if (tb>b)
{
ans+=b-a+1;
break;
}
}
ta=(long long)ta*2;
tb=(long long)tb*2+1;
}
}
printf("%lld",ans);
return 0;
}

