主成分回归（PCR）和最小二乘回归（PLS）

主成分回归（principal components regression, PCR）

#使用 p1s 库中的 pcr ()渴数实现主成分回归 (PCR)

#install.packages("pls")

library(pls)

set.seed(2)

pcr.fit=pcr(Salary~., data=Hitters,scale=TRUE,validation="CV") #设最 validation = "CV" 可以使得pcr ()函数使用十折的交叉验证计算每个可能的主成分个数M所对应的交叉验证误差。

summary(pcr.fit)

 

validationplot(pcr.fit,val.type="MSEP") #使用 validatìonplot ()函数作出交叉验证得分的图像，MSE是均方误差

 

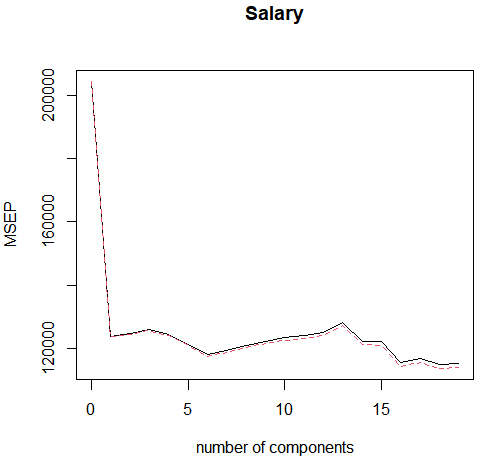
结果分析：从程序结果可以看到，当使用 M=16 个成分时，交叉验证误差最小。这个取值稍小于M=19 , M=19时 PCR 模型相当于简单最小二乘估计，因为此时在 PC模型使用了所有的成分，并没有降低数据的维度。 且是，从图像可以看到当模型中只纳入一个成分时，交叉验证误基本相同。这表明使用仅纳入少量成分的模型就足够了。

set.seed(1)

pcr.fit=pcr(Salary~., data=Hitters,subset=train,scale=TRUE, validation="CV") #在训练集上使用 PCR，并评价该方法在测试集上的使用情况。

validationplot(pcr.fit,val.type="MSEP")

 

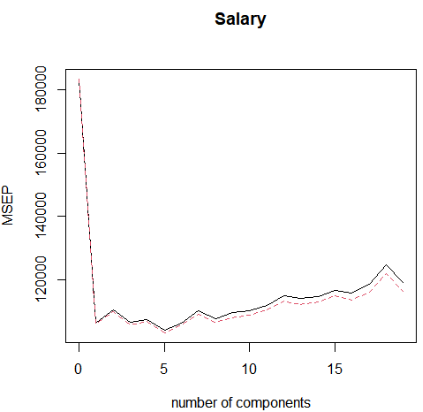
结果分析：当使用M=7个成分时，交叉验证误差最小。

pcr.pred=predict(pcr.fit,x[test,],ncomp=7)

mean((pcr.pred-y.test)^2) #计算测试集MSE

 

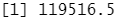
pcr.fit=pcr(y~x,scale=TRUE,ncomp=7) #在整个数据集上使用交叉验证选择出的成分个数M=7拟合PCR 模型。

summary(pcr.fit)

 

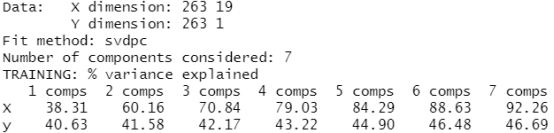
偏最小二乘回归(partial least squares,PLS)

#使用 plsr ()函数可以拟合偏最小二乘回归模型，该函数也在pls库中，其句法与pcr () 函数的句法相似。

set.seed(1)

pls.fit=plsr(Salary~., data=Hitters,subset=train,scale=TRUE, validation="CV")

summary(pls.fit)

 

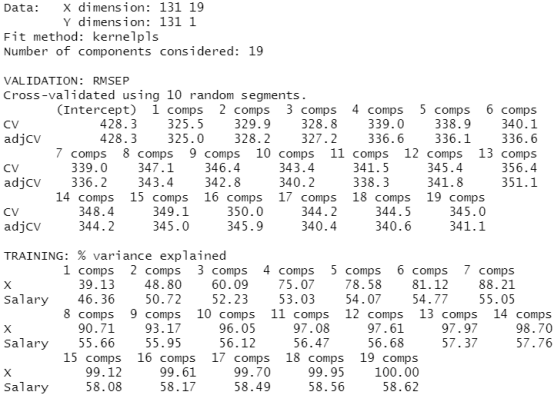
validationplot(pls.fit,val.type="MSEP")

 

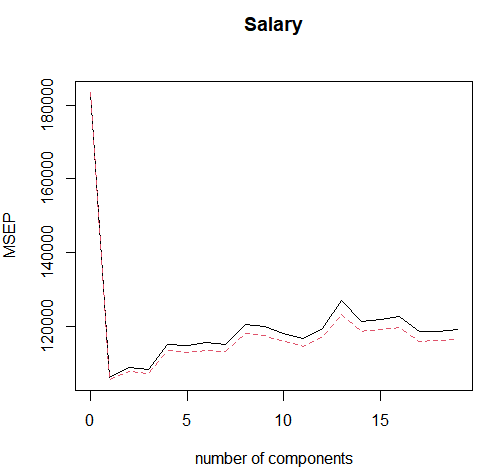
结果分析：当使用M=2个成分时，交叉验证误差最小。

pls.pred=predict(pls.fit,x[test,],ncomp=2)

mean((pls.pred-y.test)^2)

 

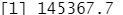
pls.fit=plsr(Salary~., data=Hitters,scale=TRUE,ncomp=2) #使用了交叉验证选取的 M=2 个成分在整个数据集上建立 PLS 模型。

summary(pls.fit)