SVM算法及案例分析（SVM分类、SVM回归）

 SVM算法的R语言实现

1.SVM分类

（1）标准分类模型

library(e1071)

data(iris)

attach(iris)

model<-svm(Species~.,data=iris) #标准分类模型

（2）多分类模型

#步骤1 数据集准备

x<-subset(iris,select = Species)

y<-Species

#步骤2 模型建立

model<-svm(x,y)

#步骤3 模型展示

summary(model)

pred<-predict(model,x)

table(pred,y)

#步骤4 多分类可视化

plot(cmdscale(dist(iris[,-5])),cex.axis=1.5,col.axis="blue",

     col.lab="red",cex.lab=1.5,col=as.integer(iris[,5]),

     pch=c("o","+")[1:150 %in% model$index+1],main="多分类可视化",

     xlab="Species",ylab="Species")

# "+"表示支持向量，"o"表示普通样本点

 

 

2. SVM回归

#步骤1 数据集准备

x<-seq(0.1,5,by=0.05)

y<-log(x)+rnorm(x,sd=0.2)

#步骤2 模型建立

m<-svm(x,y)

new<-predict(m,x)  #支持向量机2维回归模型

#步骤3 模型可视化

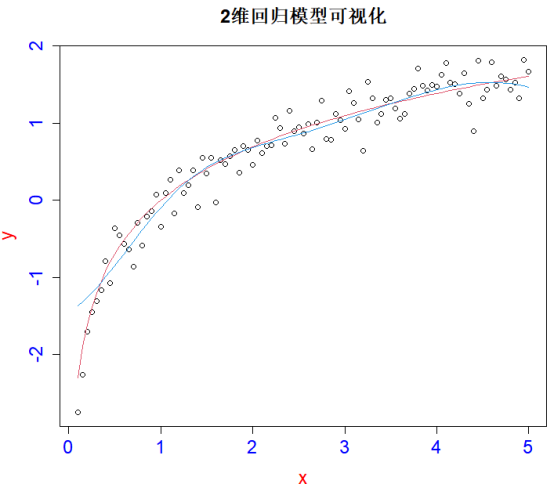
plot(x,y,main="2维回归模型可视化",cex.axis=1.5,col.axis="blue",

     col.lab="red",cex.lab=1.5,cex.main=1.5)+

     points(x,log(x),col=2,type="l")+

     points(x,new,col=4,type="l")  #回归模型建立与可视化

 

3. SVM扩展包（kernlab包）

#步骤1 加载kernlab包

library(kernlab)

#步骤2 数据集准备

#svm<-ksvm(label~.,data,kernel,kpar,C,cross)

x<-rbind(matrix(rnorm(120),,2),matrix(rnorm(120,mean = 3),,2))

y<-matrix(c(rep(1,60),rep(-1,60)))

#步骤3 模型建立与展示

svp<-ksvm(x,y,type="C-svc")

svp

 

#步骤4 模型可视化

plot(svp,data=x) #得到数据的散点分类示意图

 

案例1：SVM算法应用与iris数据据（e1071包）

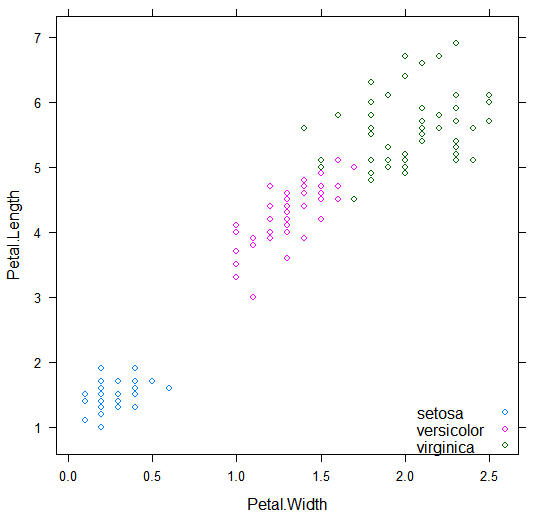
library(lattice)

library(e1071)

xyplot(Petal.Length~Petal.Width,data=iris,groups=Species,auto.key=list(corner=c(1,0))) #在正式建模之前，我们通过一个图形来初步判定数据的分布情况

  

data("iris")

attach(iris)

subdata<-iris[iris$Species!="virginica",]

subdata$Species<-factor(subdata$Species)

model<-svm(Species~Petal.Length+Petal.Width,data=subdata)

plot(model,subdata,Petal.Length~Petal.Width)

SVM算法案例分析iris数据集

#SVM算法案例

library(e1071)

data(iris)

summary(iris)

m<-svm(Species~.,data=iris) #以Species为标签，建立SVM模型

m #模型结果

 

x=iris[,-5]

y=iris[,5]

m<-svm(x,y,kernel="radial",gamma=if(is.vector(x))1 else 1/ncol(x))

summary(model)   #查看m模型的相关结果

 

pred<-predict(m,x)   #根据模型m对数据x进行预测

pred[sample(1:50,8)]   #随机挑选8个预测结果进行展示

 

table(pred,y)

 

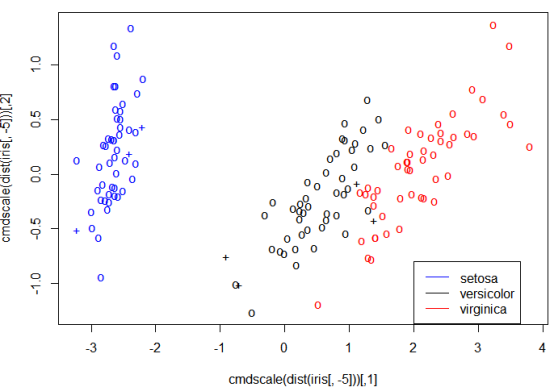
plot(cmdscale(dist(iris[,-5])),col=c("blue","black","red")

     [as.integer(iris[,5])],pch=c("o","+")[1:150 %in% model$index+1])   #SVM分类作图,"+"表示支持向量，"o"表示普通样本点

legend(2,-0.8,c("setosa","versicolor","virginica"),col=c("blue","black","red"),lty=1)

 

#plot函数还可以从其他角度对SVM模型进行可视化分析

data(iris)

model<-svm(Species~.,data=iris)

plot(model,iris,Petal.Width~Petal.Length,fill=F,

     symbolPalette=c("blue","black","red"),svSymbol="+")   #绘制模型类别关于花瓣宽度核长度的分类情况

legend(1,2.5,c("setosa","versicolor","virginica"),col=c("blue","black","red"),lty=1)

 

 

案例2：SVM算法在基因表达数据的应用

library(ISLR)

names(Khan)

 

dim(Khan$xtrain) #查看数据的维度

 

dim(Khan$xtest)

 

length(Khan$ytrain)

 

length(Khan$ytest)

 

结果分析：数据集由 2308 个基因的表达测定组成，训练集和测试集分别由 63和 20 个观测组成。

table(Khan$ytrain)  #训练集中的类别及观测数目

 

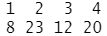
table(Khan$ytest) ##测试集中的类别及观测数目

 

#在这个数据集中，相对于观测的数目来说，特征的数目非常多，基于这一特点建议使用线性核函数，因为使用多项式核函数和径向核函数得到更高光滑性是没有必要的。

dat=data.frame(x=Khan$xtrain, y=as.factor(Khan$ytrain)) #训练数据集

out=svm(y~., data=dat, kernel="linear",cost=10)

summary(out)

 

table(out$fitted, dat$y) #训练集混淆矩阵

 

结果分析：混淆矩阵结果显示，训练集的误装为0，事实上，这并不奇怪，因为相对于观测的数目来说，变量的数目较多意味着很容易找到把这些类别完全分开的超平面。

dat.te=data.frame(x=Khan$xtest, y=as.factor(Khan$ytest)) #测试集

pred.te=predict(out, newdata=dat.te)

table(pred.te, dat.te$y) #测试集混淆矩阵

 

结果分析：混淆矩阵结果显示，测试集中有2个样本被错误分类了。