判别分析--费希尔判别、贝叶斯判别、距离判别

判别分析

比较理论一些来说，判别分析就是根据已掌握的每个类别若干样本的数据信息，总结出客观事物分类的规律性，建立判别公式和判别准则;在遇到新的样本点时，再根据已总结出来的判别公式和判别准则，来判断出该样本点所属的类别。

1  概述

三大类主流的判别分析算法，分别为费希尔(Fisher)判别、贝叶斯(Bayes)判别和距离判别。

具体的，在费希尔判别中我们将主要讨论线性判别分析（Linear Discriminant Analysis，简称LDA）及其原理一般化后的衍生算法，即二次判别分析（Quadratic Discriminant Analysis，简称QDA);而在贝叶斯判别中将介绍朴素贝叶斯分类(Naive Bayesian Classification)算法;距离判别我们将介绍使用最为广泛的K最近邻(k-Nearest Neighbor，简称kNN)及有权重的K最近邻( Weighted k-Nearest Neighbor）算法。

1.1 费希尔判别

费希尔判别的基本思想就是“投影”，即将高维空间的点向低维空间投影，从而简化问题进行处理。

投影方法之所以有效，是因为在原坐标系下，空间中的点可能很难被划分开，如下图中，当类别Ⅰ和类别Ⅱ中的样本点都投影至图中的“原坐标轴”后，出现了部分样本点的“影子”重合的情况，这样就无法将分属于这两个类别的样本点区别开来;而如果使用如图8-2中的“投影轴”进行投影，所得到的“影子”就可以被“类别划分线”明显地区分开来，也就是得到了我们想要的判别结果。

 

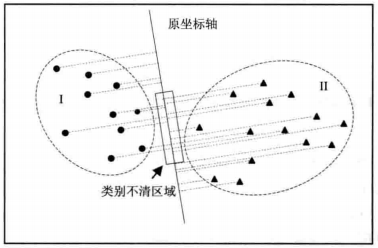
                                 原坐标轴下判别

 

                                投影轴下判别

我们可以发现，费希尔判别最重要的就是选择出适当的投影轴，对该投影轴方向上的要求是:保证投影后，使每一类之内的投影值所形成的类内离差尽可能小，而不同类之间的投影值所形成的类间离差尽可能大，即在该空间中有最佳的可分离性，以此获得较高的判别效果。

对于线性判别，一般来说，可以先将样本点投影到一维空间，即直线上，若效果不明显，则可以考虑增加一个维度，即投影至二维空间中，依次类推。而二次判别与线性判别的区别就在于投影面的形状不同，二次判别使用若干二次曲面，而非直线或平面来将样本划分至相应的类别中。

相比较来说，二次判别的适用面比线性判别函数要广。这是因为，在实际的模式识别问题中，各类别样本在特征空间中的分布往往比较复杂，因此往往无法用线性分类的方式得到令人满意的效果。这就必须使用非线性的分类方法，而二次判别函数就是一种常用的非线性判别函数，尤其是类域的形状接近二次超曲面体时效果更优。

1.2 贝叶斯判别

朴素贝叶斯的算法思路简单且容易理解。

理论上来说，它就是根据已知的先验概率 P(A|B)，利用贝叶斯公式

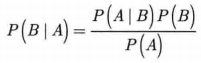
求后验概率P(B|A)，即该样本属于某一类的概率，然后选择具有最大后验概率的类作为该样本所属的类。

通俗地说，就是对于给出的待分类样本，求出在此样本出现条件下各个类别出现的概率，哪个最大，就认为此样本属于哪个类别。

朴素贝叶斯的算法原理虽然“朴素”，但用起来却很有效，其优势在于不怕噪声和无关变量。而明显的不足之处则在于，它假设各特征属性之间是无关的，当这个条件成立时，朴素贝叶斯的判别正确率很高，但不幸的是，在现实中各个特征属性间往往并非独立，而是具有较强相关性的，这样就限制了朴素贝叶斯分类的能力。

1.3 距离判别

距离判别的基本思想，就是根据待判定样本与已知类别样本之间的距离远近做出判别。具体的，即根据已知类别样本信息建立距离判别函数式，再将各待判定样本的属性数据逐一代入计算，得到距离值，根据距离值将样本判入距离值最小的类别的样本簇。

K最近邻算法则是距离判别中使用最为广泛的，即如果一个样本在特征空间中的K个最相似/最近邻的样本中的大多数属于某一个类别，则该样本也属于这个类别。

K最近邻方法在进行判别时，由于其主要依靠周围有限邻近样本的信息，而不是靠判别类域的方法来确定所属类别，因此对于类域的交叉或重叠较多的待分样本集来说，该方法较其他方法要更为适合。