自助法--boot 包

1 自助法

所谓自助法，即从初始样本重复随机替换抽样，生成一个或一系列待检验统计量的经验分布。

无需假设一个特定的理论分布，便可生成统计量的置信区间，并能检验统计假设。倘若你假设均值的样本分布不是正态分布，该怎么办呢？可使用自助法。

(1) 从样本中随机选择10个观测，抽样后再放回。有些观测可能会被选择多次，有些可能一直都不会被选中。

(2) 计算并记录样本均值。

(3) 重复1和2一千次。

(4) 将1000个样本均值从小到大排序。

(5) 找出样本均值2.5%和97.5%的分位点。此时即初始位置和最末位置的第25个数，它们就限定了95%的置信区间。

2 boot 包中的自助法

boot包扩展了自助法和重抽样的相关用途。你可以对一个统计量（如中位数）或一个统计

量向量（如一列回归系数）使用自助法。

一般来说，自助法有三个主要步骤。

(1) 写一个能返回待研究统计量值的函数。如果只有单个统计量（如中位数），函数应该返回一个数值；如果有一列统计量（如一列回归系数），函数应该返回一个向量。

(2) 为生成R中自助法所需的有效统计量重复数，使用boot()函数对上面所写的函数进行处理。

(3) 使用boot.ci()函数获取步骤(2)生成的统计量的置信区间。

主要的自助法函数是boot()，它的格式为：

bootobject <- boot(data=, statistic=, R=, ...)

 

boot()函数调用统计量函数R次，每次都从整数1:nrow(data)中生成一列有放回的随机指标，这些指标被统计量函数用来选择样本。

你可以用bootobject$t0和bootobject$t这样来获取这些元素。一旦生成了自助样本，可通过print()和plot()来检查结果。如果结果看起来还算合理，使用boot.ci()函数获取统计量的置信区间。格式如下：

boot.ci(bootobject, conf=, type= )

 

type参数设定了获取置信区间的方法。perc方法（分位数）展示的是样本均值，bca将根据偏差对区间做简单调整。bca在大部分情况中都是更可取的。

3  对单个统计量使用自助法

以mtcars数据集为例，它有11个变量，包含32辆汽车的信息。假设你正使用多元回归根据车重wt和发动机排量mpg来预测汽车每加仑行驶的英里数disp，除了标准的回归统计量，你还想获得95%的R平方值的置信区间（预测变量对响应变量可解释的方差比），那么便可使用非参数的自助法来获取置信区间。

（1）首先是写一个获取R平方值的函数：

rsq <- function(formula, data, indices) {

  d <- data[indices,]

  fit <- lm(formula, data=d)

  return(summary(fit)$r.square)

}

函数返回回归的R平方值。d <- data[indices, ]必须声明，因为boot()要用其来选择样本。

（2）做大量的自助抽样（比如1000），代码如下：

library(boot)

set.seed(1234)

results <- boot(data=mtcars, statistic=rsq, R=1000, formula=mpg~wt+disp)

（3）boot的对象可以输出，代码如下：

print(results)

 

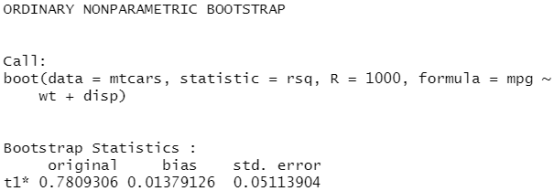
也可用plot(results)来绘制结果：

 

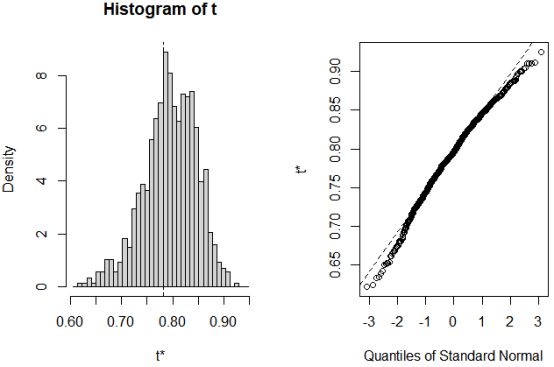
图中可以看到，自助的R平方值不呈正态分布。它的95%的置信区间可以通过如下代码获得：

 boot.ci(results, type=c("perc", "bca"))

 

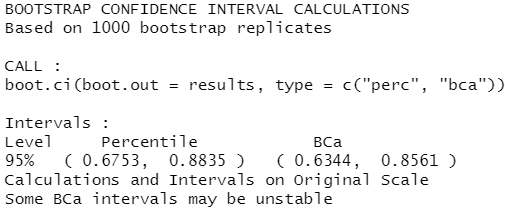
结果分析：从该例可以看到，生成置信区间的不同方法将会导致获得不同的区间。本例中的依偏差调整区间方法与分位数方法稍有不同。