Mini-batch 梯度下降（Mini-batch gradient descent）

Mini-batch 梯度下降（Mini-batch gradient descent）

 

  向量化能够让你相对较快地处理所有m个样本。如果m很大的话，处理速度仍然缓慢，如果m是 500 万或 5000 万或者更大的一个数，在对整个训练集执行梯度下降法时，你要做的是，你必须处理整个训练集，然后才能进行一步梯度下降法，所以如果你在处理完整个 500 万个样本的训练集之前，先让梯度下降法处理一部分，你的算法速度会更快。

我们可以把训练集分割为小一点的子集训练，这些子集被取名为 mini-batch，假设每一个子集中只有 1000 个样本，那么把其中的x⁽¹⁾到x⁽¹⁰⁰⁰⁾取出来，称为X^{1}，将其称为第一个子训练集，也叫做 mini-batch，然后你再取出接下来的 1000 个样本，从x⁽¹⁰⁰¹⁾到x⁽²⁰⁰⁰⁾，称为X^{2}，然后再取 1000个样本，以此类推，每个 mini-batch 都有 1000 个样本。对Y也要进行相同处理，你也要相应地拆分Y的训练集，所以这是Y^{1}，然后从y⁽¹⁰⁰¹⁾到y⁽²⁰⁰⁰⁾，这个叫Y^{2}，一直到Y^{5000}。

 

上角小括号(i)表示训练集里的值，所以x⁽ⁱ⁾是第i个训练样本，我们用了上角中括号[l]来表示神经网络的层数，z^[l]表示神经网络中第l层的z值，我们现在引入了大括号t来代表不同的mini-batch，所以我们有X^{t}和Y^{t}。X^{t}和Y^{t}的维数：如果X^{1}是一个有 1000 个样本的训练集，或者说是 1000 个样本的x值，所以维数应该是(n_x, 1000)，X^{2}的维数应该是(n_x, 1000)，以此类推，因此所有的子集维数都是(n_x, 1000)，而这些（Y^{t}）的维数都是(1,1000)。

 

mini-batch 梯度下降法，指的是每次同时处理的单个的 mini-batch X^{t}和Y^{t}，而不是同时处理全部的X和Y训练集.首先对输入也就是X^{t}，执行前向传播，然后执行z^[1] = w^[1]x + b^[1]，你在处理第一个 mini-batch，时它变成了X^{t}，即z^[1] = w^[1]x^{t} + b^[1]，然后执行A^[1]k = g^[1](Z^[1])，之所以用大写的Z是因为这是一个向量内涵，以此类推，直到A^[L] = g^[L](Z^[L])，这就是我们的预测值；接下来你要计算损失成本函数J，因为子集规模是 1000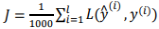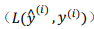，, 指的是来自于 mini-batch  X^{t}和Y^{t}中的样本，如果你用到了正则化，可以使用正则化的术语，因为这是一个 mini-batch 的损失，所以我将J损失记为上角标t，放在大括号里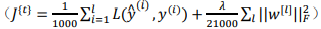，接下来，你执行反向传播来计算J^{t}的梯度，你只是使用X^{t}和Y^{t}，然后你更新加权值，w实际上是w^[t]，更新为：w^[l]:=w^[l]=adw^[l]，对b做相同处理：b^[l]:=b^[l]=adb^[l] 。

 

使用 batch 梯度下降法时，每次迭代你都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数J是迭代次数的一个函数，它应该会随着每次迭代而减少，如果J在某次迭代中增加了，那肯定出了问题，也许你的学习率太大。使用 mini-batch 梯度下降法，则并不是每次迭代都是下降的，会出现一些摆动，但整体趋势是向下的，它不会总朝向最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向。

 

如果训练集较小，直接使用 batch 梯度下降法，你可以快速处理整个训练集，比如少于2000个样本。在 mini-batch 中，要确保X^{t}和Y^{t}，要符合 CPU/GPU 内存，取决于你的应用方向以及训练集的大小。