回归分析1（回归分析、回归诊断、模型综合验证）

1 OLS回归（最小二乘法回归）

1.1 用lm()拟合回归模型

在R中，拟合线性模型最基本的函数是lm()，格式为：myfit<-lm(formula,data)

1.2 简单线性回归

dat<-women

fit<-lm(weight~height,data=dat)

summarize(fit)

 

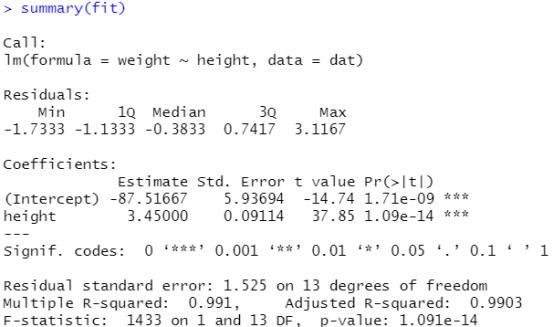
结果分析：回归方程weight = 3.45 height - 87.51667，这两个估计值是否可靠呢，需要看Pr(>|t|)值，p值小于0.05，我们就认为它在95%的置信区间上是不为0的，它的统计是显著的，简单一点，只要有星星，结果就可以认为是可靠的，看拟合优度Adjusted R-squared：0.9903，结果是非常好的，p-value是对整个方程的估计， p-value: 1.091e-14<0.05可以认为结果是可靠的。

plot(dat$height,dat$weight)  #查看height和weight的散点图（实际散点图）

abline(fit)  #画回归线，查看拟合结果（估计出来的线）

 

结果分析：散点图是实际的数据，回归线基本在散点图附近，说明拟合效果比较好

1.3 多项式回归（身高和体重的平方）

fit1<-lm(weight~height+I(height^2),data=dat)   #为了防止错误识别^，加了一个I()函数，指出^是一个常规得符号

summary(fit1)

 

结果分析：回归方程weight = -7.34832height + 0.08306height^2 + 261.87818，这两个估计值是否可靠，需要看Pr(>|t|)值，p值小于0.05，我们就认为它在95%的置信区间上是不为0的，它的统计是显著的，简单一点，只要有星星，结果就可以认为是可靠的，看拟合优度Adjusted R-squared：0.9994，结果是非常好的，p-value是对整个方程的估计， p-value:  2.2e-16<0.05可以认为结果是可靠的，对比上一个可以看出这个拟合优度更高

plot(dat$height,dat$weight)  #画散点图

lines(dat$height,fitted(fit1))  #使用函数lines()画线，abline()只适用于一元，要给出横坐标dat$height，纵坐标fitted(fit1)

 

1.4 多元线性回归（预测变量不止一个）

states<-as.data.frame(state.x77[,c("Murder",

           "Population","Illiteracy","Income","Frost")])

cor(states)  #列出是所有列变量两两之间的相关系数

 

 画出全部两两变量之间的关系：

library(car)

scatterplotMatrix(states,spead=F,smooth.args=list(lty=2)

 

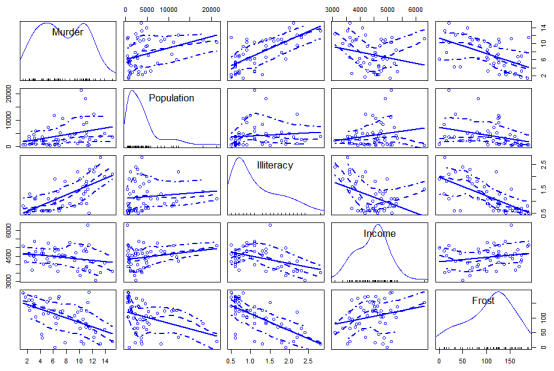
结果分析：对角线是单变量自己的分布情况，其他情况虽然点很复杂，但上面清晰的描述了一条实线，大致说明了变量之间的关系 

fit2<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)  #回归分析，Murder是预测变量，Population+Illiteracy+Income+Frost是解释变量

summary(fit2)

 

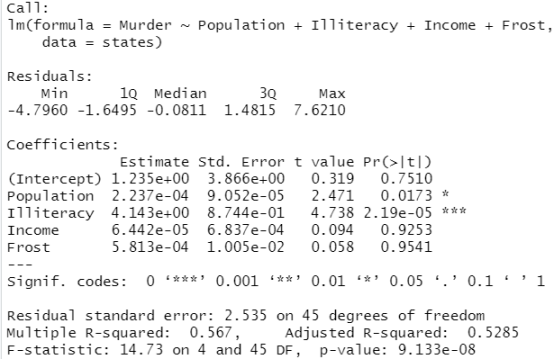
结果分析：Murder与Population和Illiteracy的关系后面的Pr(>|t|)小于0.05，后面有星星，说明他们之间的关系是显著的，Murder与Income和Frost的关系后面的Pr(>|t|)大于0.05，后面也没有星星，说明其关系不显著，并且Income和Frost前面的系数 Estimate是正的，说明其与Murder是正相关，但是从上面的散点图可以看出，估计出来的直线是向下的，即呈现负相关性，所以可以认为Murder与Income和Frost没什么关系。

 

错误：下标出界

 

修正：检查列名是否写正确

 

1.1 有交互项的多元线性回归

交互项：响应变量与其中一个预测变量的关系还依赖另外一个预测变量的水平

fit3<-lm(mpg~hp+wt+hp:wt,data=mtcars)  #回归分析，交互项用冒号 ：连接

summary(fit3)

 

结果分析：可以看出mpg与hp和wt以及它们的交互项hp:wt都是有关系的，后面有星星，三颗星表示关系是最好的

2 回归诊断

states<-as.data.frame(state.x77[,c("Murder",

           "Population","Illiteracy","Income","Frost")])

fit2<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)  #回归分析，Murder是预测变量，Population+Illiteracy+Income+Frost是解释变量

summary(fit2)

confint(fit2)   #给出区间估计，95%的可能

 

2.1 标准方法

dat<-women  #确定数据集

fit<-lm(height~weight,data=dat)  #做回归分析

summary(fit) 

opar<-par(no.readonly = T)

par(mfrow=c(2,2))  #画图

plot(fit) 

结果分析：右上角是Q-Q图，反应样本的正态性，样本散点图呈一条直线，基本认定是服从正太假设的；左上图是观察样本的线性问题的，很明显这个呈现是二次曲线，不满足线性；左下角图是观察样本的同方差性，如果是同方差性，这个线会在散点图的上下两侧波动，这个图是符合的；右下角图是独立性，观察离群值

dat<-women

fit1<-lm(weight~height+I(height^2),data=dat)

opar<-par(no.readonly = T)

par(mfrow=c(2,2))

plot(fit1)

 

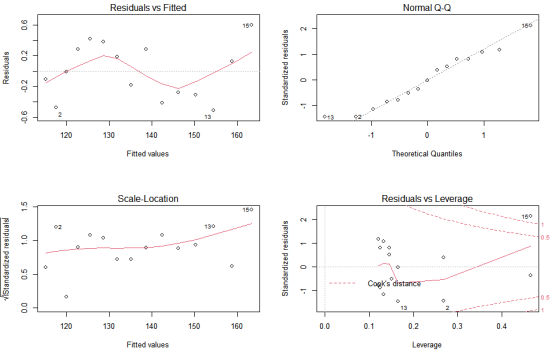
结果分析：右上角是Q-Q图，反应样本的正态性，样本散点图呈一条直线，基本认定是服从正太假设的；左上图是观察样本的线性问题的，这次是拟合weight与height平方之间的关系，可以看出基本满足线性；左下角图是观察样本的同方差性，如果是同方差性，这个线会在散点图的上下两侧波动，这个图是符合的；右下角图是独立性，观察离群值

2.2 改进方法

library(car)

（1）正态性

states<-as.data.frame(state.x77[,c("Murder",

           "Population","Illiteracy","Income","Frost")])

fit2<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)  #回归分析，Murder是预测变量，Population+Illiteracy+Income+Frost是解释变量

summary(fit2)

par(mfrow=c(1,1)) #把绘图区域恢复

qqplot(fit2,labels=row.names(states),id.mentod="identify",

       simulate=T,main="QQ plot")

结果分析：大多数点置信区间（两条虚线之间）范围内，点基本在一条直线上，我们可以认为此样本基本符合正太分布

这个州 Nevada 的估计值：

 

这个州 Nevada 的实际值：

 

结论：这个州的估计和实际差别很大，在实际应用中可以当离群点删掉

 

错误：种类'list'目前没有在'greater'里实现

 

修正：这里是为什么呢？？

      后来仔细检查了语句，单词大小写错了

 

 （2）独立性

states<-as.data.frame(state.x77[,c("Murder",

           "Population","Illiteracy","Income","Frost")])

fit2<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)  #回归分析，Murder是预测变量，Population+Illiteracy+Income+Frost是解释变量

durbinWatsonTest(fit2)

 

 结论分析：我们希望p-value的值越大越好，如何很大，就说明不相关，即互相独立，基本上我们可以认为这些变量是互相独立的

（3）线性

states<-as.data.frame(state.x77[,c("Murder",

                                   "Population","Illiteracy","Income","Frost")])

fit2<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)

par(mfrow=c(2,2))

crPlots(fit2)  #画成分残差图

 

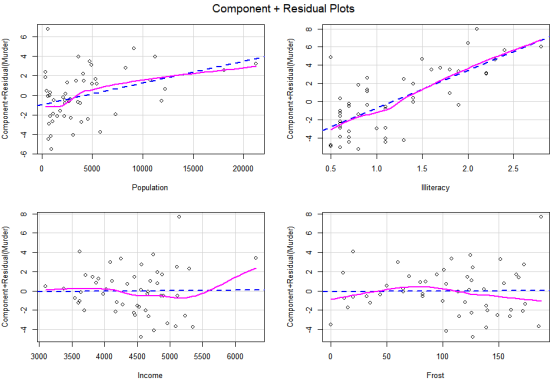
结果分析：虚线是直线，是最小二乘法估计，我们需要看实线是否与虚线基本重合，若基本重合，我们认为是呈线性关系的

（4）同方差性

 ncvTest(fit2)

 

结果分析：跟上面一样，P值越大越好，P越大说明其是同方差性的，满足假设

2.3 线性模型假设的综合验证

install.packages("gvlma")

library(gvlma)

states<-as.data.frame(state.x77[,c("Murder",

           "Population","Illiteracy","Income","Frost")])

fit2<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)  #回归分析，Murder是预测变量，Population+Illiteracy+Income+Frost是解释变量

gvmodel<-gvlma(fit2)

summary(gvmodel)

 

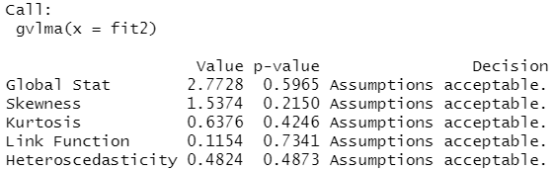
结果分析：这里后面都是acceptable，若是不接受，要一个个检查上面四个图

2.3.1 多重共线性

vif(fit2) 

 

结果分析：计算出这四个方差膨胀因子，书本上认为小于4就可以，实际上我们还是会计算一下相关系数

cor(states)  #做两两变量之间的相关性系数的比较

 

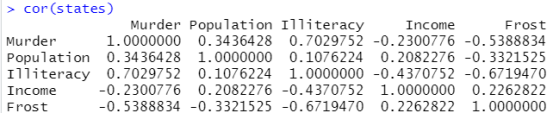
结果分析：一般对角线上的值越大越好，除对角线以外的矩阵数字最好不要大于0.7