有向图的拓扑排序——BFS

假设你有n个任务要做，其中某些任务需要在另外一些任务之前完成，你该如何规划你的任务，使得按照你的规划依次做下去就能完成你的所有任务？

定义

拓扑排序（Topological sorting, toposort）：给定一个有向无环图，将所有节点排成一个线性序列，在这个序列中只有从前面的节点指向后面的节点的边。

条件

有向图中没有环。如果有环的话就无法进行拓扑排序。因为如果尝试将所有节点排成一个线性序列的话，就必然会出现这种情况：

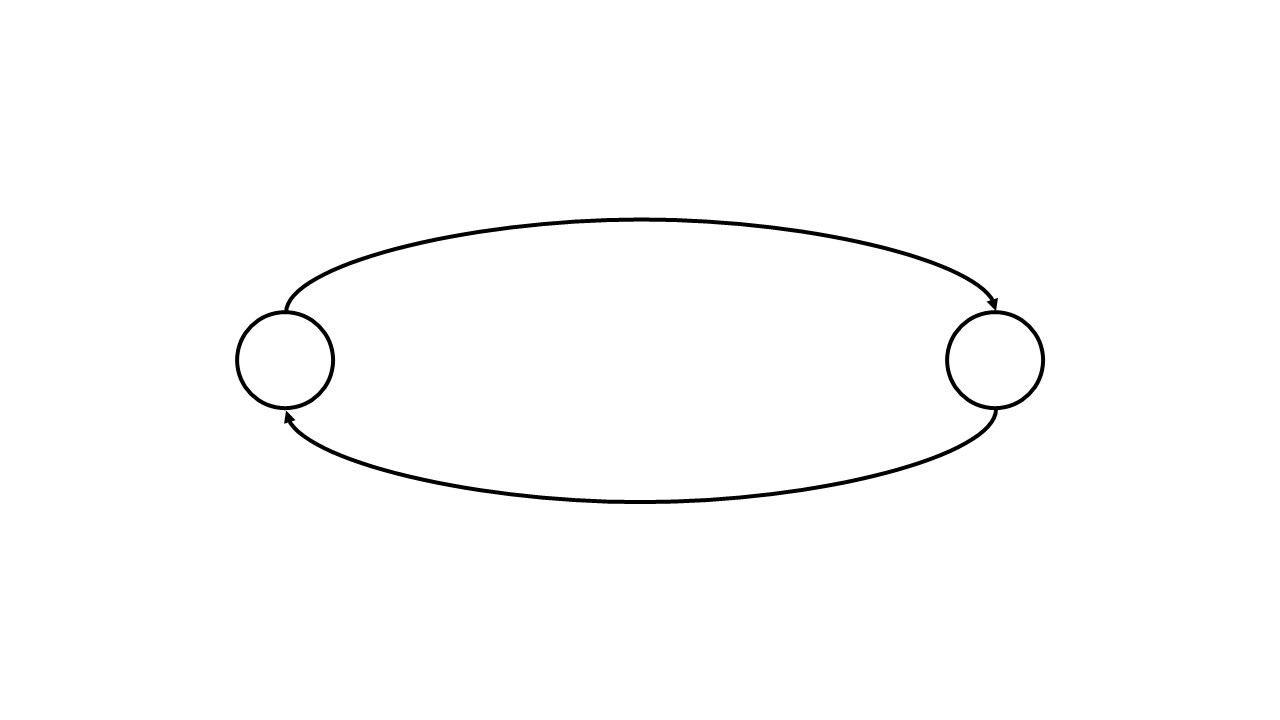
必然有从后面的节点指向前面的节点的有向边，不符合拓扑排序的定义，所以无法对有环的有向图进行拓扑排序。

假如你手边有两个任务A和B，要完成任务A你得先完成任务B，要完成任务B你又得先完成任务A，你一定会觉得这很刁钻，对吧？

注意一张图的拓扑排序并不是唯一的，比如下面这张图：

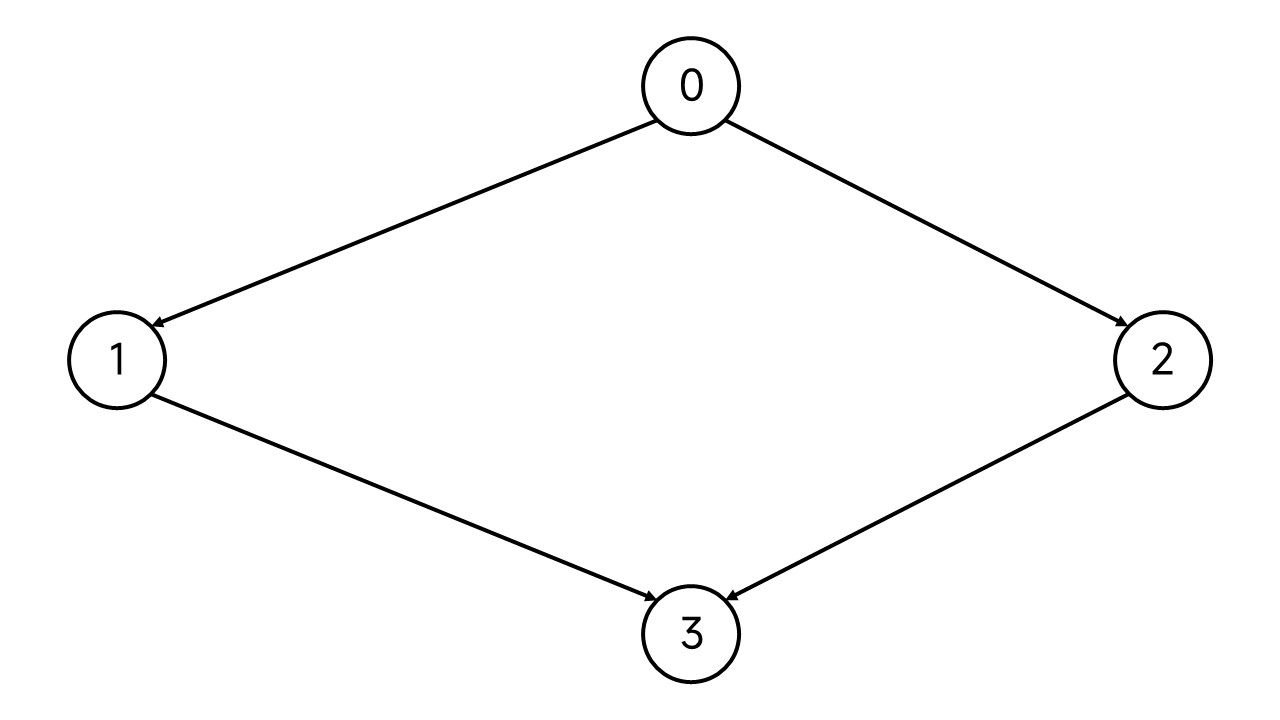
序列 0 1 2 3 和 0 2 1 3 均是合法的拓扑排序序列，只要1和2出现在0之后3之前即可，内部的顺序无所谓。

方法

拓扑排序有多种方法，BFS（广度优先搜索）是其中的一种。

以下面这张图为例：

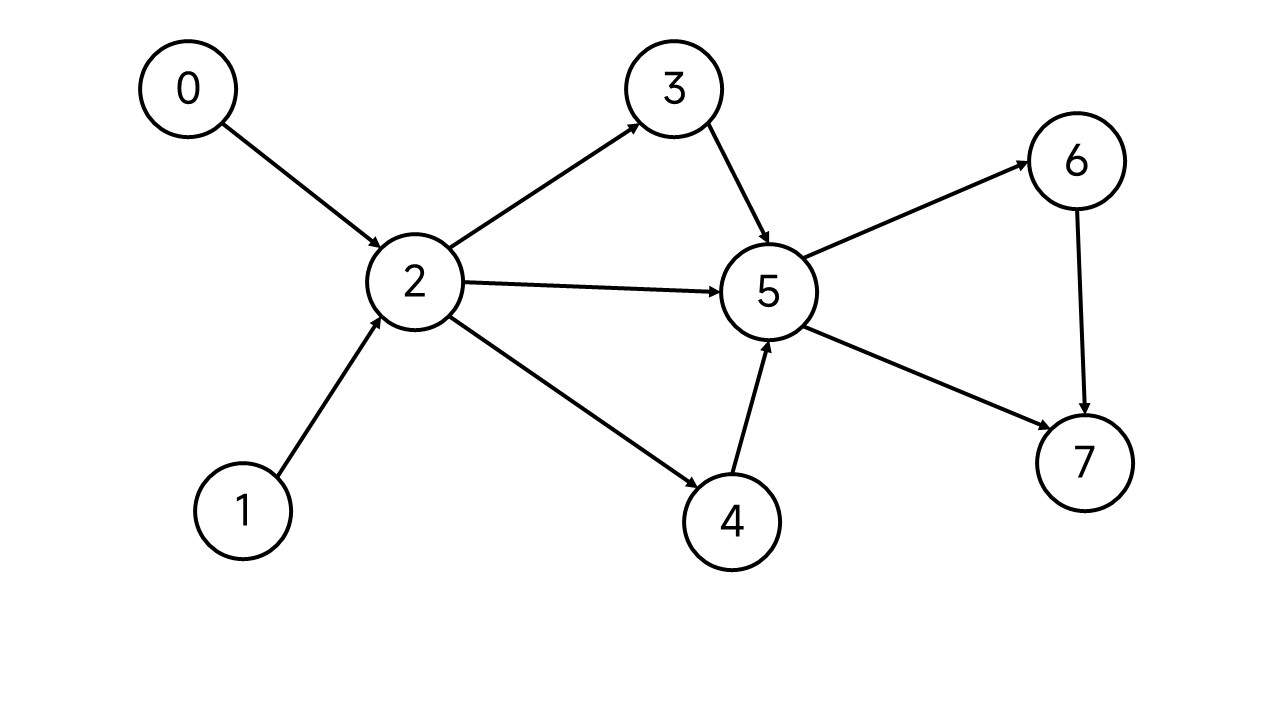
最先完成的任务之前没有需要完成的任务，用图论的语言来说就是拓扑排序序列的第一个节点没有入边，入度为0。在这张图中，入度为0的节点有两个：节点0和节点1，将这两个节点添加到序列中。

任务完成之后，就不需要考虑了，我们可以直接将这两个节点从图中移除。

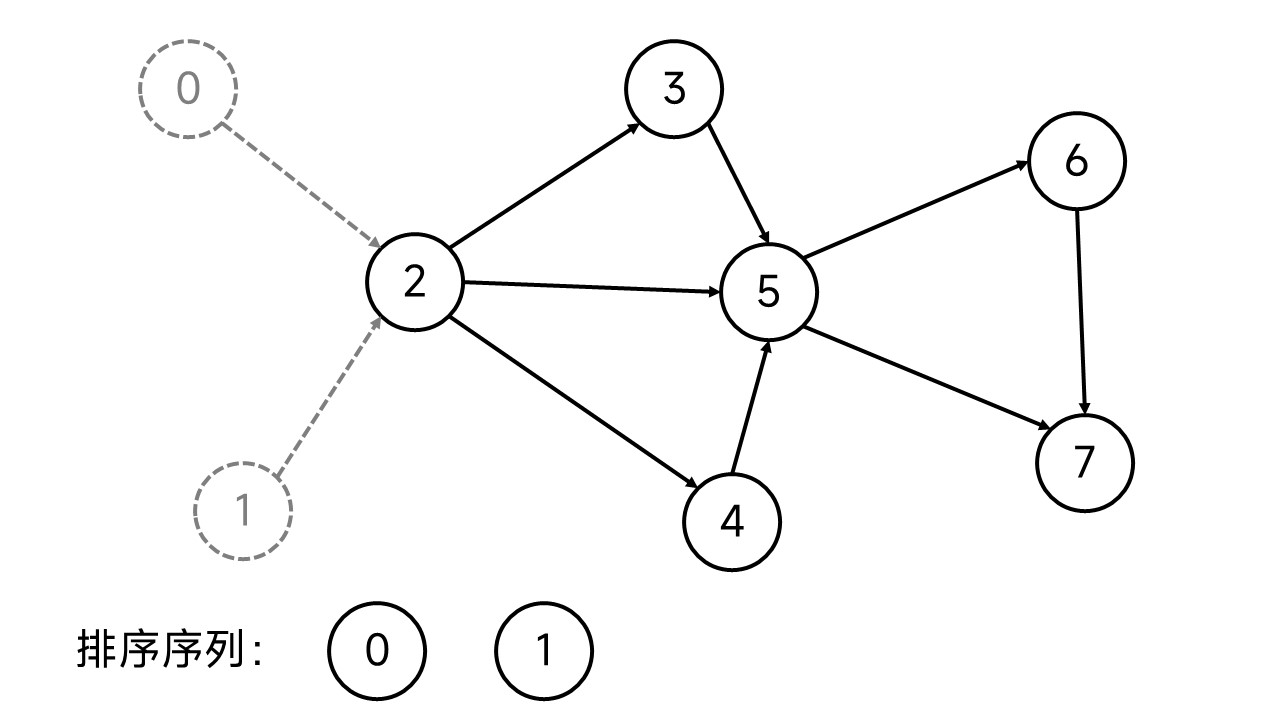
这时，节点2就变成0入度节点了，继续同样的步骤。一直这样重复下去，直到图中没有剩余的节点为止。这样，我们就得到了这样一个拓扑排序序列：

0 1 2 3 4 5 6 7

所以，整个拓扑排序算法如下：

1. 寻找0入度节点，从图中移除并添加到拓扑排序序列。
2. 重复上述步骤，直到图中没有剩余的节点。

算法及代码实现

为了使语义更加明确，我们先定义类型别名node_t，代表unsigned long long：

using node_t = unsigned long long;

因为整个算法主要利用的是两个节点之间的邻接关系，我们在这里使用邻接表来表示整个图。同时使用邻接表需要的空间花销更少。

class Graph {
    unsigned long long n;
    vector<vector<node_t>> map;

public:
    Graph(initializer_list<initializer_list<node_t>> list) : n(list.size()), map({}) {
        for (auto &l : list) {
            map.emplace_back(l);
        }
    }

    vector<node_t> toposort();
};

为了不破坏整个图的结构，我们单独开一个数组来存放所有节点的入度。伪代码如下：

初始化入度数组S
for (节点v : 节点集合V) {
    for (节点v’ : 以节点V为起点的所有有向边的终点集合V’) {
        S[v’]++
    }
}

代码：

vector<node_t> inDegrees(n, 0);
for (auto &ends : map) {
    for (node_t end : ends) {
        inDegrees[end]++;
    }
}

注意到某一时刻0入度节点可能不止1个，因此我们需要某种数据结构来“暂存”这些0入度节点。又注意到0入度节点总是先出现后被移除并加入到序列，因此我们的Mr. Right就是具有“先入后出”性质的队列。

伪代码：

初始化队列Q
for (节点v : 节点集合V) {
    if (节点v的入度为0) {
        将节点v加入到队列Q中
    }
}

代码：

queue<node_t> zeroInDegree;
for (node_t node = 0; node < n; node++) {
    if (inDegrees[node] == 0) {
        zeroInDegree.push(node);
    }
}

接下来，我们只需要将队列头部节点移除并加入到排序序列，并相应的更新该节点指向的节点的入度。如果指向的节点的入度减为零了，那就添加到队列中。

伪代码：

令队列Q的头部节点为v’
将v’弹出队列并加入到拓扑排序序列
for (节点v’’ : v’指向的所有节点集合) {
    v’’的入度减一
    if (v’’的入度 == 0) {
        将v’’加入队列Q
    }
}

代码：

node_t v = zeroInDegree.front();
zeroInDegree.pop();
sort.push_back(v);
for (node_t end : map[v]) {
    inDegrees[end]--;
    if (inDegrees[end] == 0) {
        zeroInDegree.push(end);
    }
}

如此重复下去，如果队列变空了，则说明已经将所有的节点都加入到序列中了，算法结束。

整个算法的伪代码：

初始化入度数组S、队列Q和拓扑排序序列T
for (节点v : 节点集合V) {
    for (节点v’ : 以节点V为起点的所有有向边的终点集合V’) {
        S[v’]++
    }
}
for (节点v : 节点集合V) {
    if (S[v’] == 0) {
        将节点v加入到队列Q中
    }
}
令队列Q的头部节点为v’
将v’弹出队列并加入到拓扑排序序列
for (节点v’’ : v’指向的所有节点集合) {
    S[v’’]--
    if (S[v’’] == 0) {
        将v’’加入队列Q
    }
}

代码：

vector<node_t> Graph::toposort() {
    vector<node_t> inDegrees(n, 0);
    queue<node_t> zeroInDegree;
    vector<node_t> sort;
    for (auto &ends : map) {
        for (node_t end : ends) {
            inDegrees[end]++;
        }
    }
    for (node_t node = 0; node < n; node++) {
        if (inDegrees[node] == 0) {
            zeroInDegree.push(node);
        }
    }
    while (!zeroInDegree.empty()) {
        node_t v = zeroInDegree.front();
        zeroInDegree.pop();
        sort.push_back(v);
        for (node_t end : map[v]) {
            inDegrees[end]--;
            if (inDegrees[end] == 0) {
                zeroInDegree.push(end);
            }
        }
    }
    return sort;
}

测试：

int main() {
    Graph graph{
            {2},
            {2},
            {3, 4, 5},
            {5},
            {5},
            {6, 7},
            {7},
            {}
    };
    auto sort = graph.toposort();
    for (auto node : sort) {
        cout << node << ' ';
    }
    cout << endl;
    return 0;
}

复杂度分析

时间复杂度：O(n+e)，其中n为顶点数，e为边数。这主要取决于寻找0入度节点所需要的时间花销。

空间复杂度：O(n+e)，其中n为顶点数，e为边数。这主要取决于邻接表所需要的空间花销。