【学习记录】用电池问题及其解答
用电池问题指的是这样的一类问题:
你有一台游戏机,这台游戏机需要同时装上$k$节电池才能正常工作。
你现在有$n$节电池,每节电池的电量是$a_i$,代表它在使用$a_i$分钟之后会没电。
你可以在任意时刻更换游戏机中的电池,这个时刻不一定是整数,更换电池的操作不占用时间。
现在请问这台游戏机最多能正常工作多久?答案保留三位小数。
这是一道计算概论期末考试中出现的问题,我在考场上思考$1h$无果,于是在考后学习了一下。
对于这一类看起来不知道是什么问题的问题,我们应当考虑通过手算几个样例来理解题目的本质。
在本题中,最简单的样例是$k=1$,此时所求答案就是$\sum \limits_{i=1}^{n}a_i$。
第二简单的样例是$k=2$,此时我们是否可以断言所求答案是$\frac{1}{2}\sum \limits_{i=1}^{n}a_i$?
事实上这是不能的。比如当$n=2$,且两节电池电量不一样的时候,那么多的那一节多出来的部分就会被浪费掉。
于是我们自然而然地考虑一个问题:什么时候会出现电池电量被浪费掉的情况呢?
为方便考虑,下面我们令$a_1 < a_2 < \cdots <a_n$。
首先注意到假如$\sum \limits_{i=1}^{n-1}a_i <a_n$,那么$a_n$就一定会有一部分电量($a_n - \sum \limits_{i=1}^{n-1}a_i $)被浪费掉。
那么如果$\sum \limits_{i=1}^{n-1}a_i \geq a_n$呢?此时我们确实能够得到结论:$a_n$不会有电量被浪费掉。
下面给出这个结论的证明:
注意到满足上述条件时有$\frac{1}{2}\sum \limits_{i=1}^{n}a_i\geq a_n$,
从而我们考虑一种安排电池的方案能恰好用满$\frac{1}{2}\sum \limits_{i=1}^{n}a_i$这么长的时间:
- 先把$a_n$安排到第一个电池位。
- 再把$a_{n-1}$拆成两部分,一部分用来补第一个电池位缺的部分,另一部分安排到第二个电池位。
- 以此类推安排$a_{n-2},\cdots,a_1$。
- 最后按照安排的方案装填游戏机即可。(具体方案见下图)
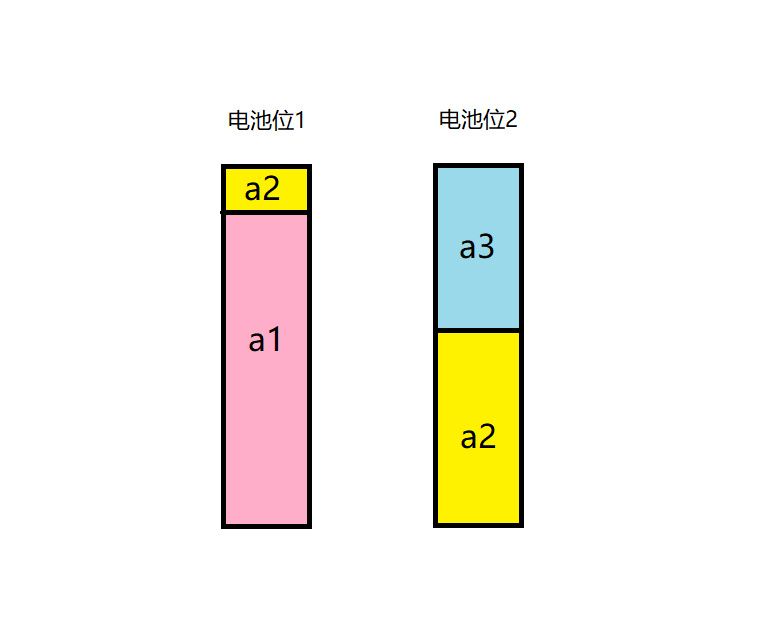
如果安排好之后的方案是这样,那么装游戏机的方案就是(我们认为开始时刻在最底下,结束时刻在最上面):
- 从开始到电池位2的$a_2$用完的这段时间,我们用电池$(a_1,a_2)$。
- 从电池位2的$a_2$用完到电池位1的$a_1$用完的这段时间,我们用电池$(a_1,a_3)$。
- 从电池位1的$a_1$用完到结束的这段时间,我们用电池$(a_2,a_3)$。
如果按这种电池位的方式看这个问题,容易发现一种方案不合法当且仅当某一节电池在某一时刻同时出现在两个电池位。
而根据我们的安排方式,某一节电池如果出现在两个电池位,那么在其中一个电池位里它必然是最后一段时间使用的,而在另外一个电池位里它必然是最前一段时间使用的。
而如果这样都不合法,那么必然有$a_i >\frac{1}{2}\sum \limits_{i=1}^{n}a_i$。
根据我们前面的假定知道不存在这样的$a_i$,从而这个方案必然合法,证毕。
根据这个证明也可以看出,此时不仅$a_n$不会有电量被浪费掉,任何一节电池都不会有电量被浪费掉。
从而我们就解决了$k=2$时的问题:
- 如果$\sum \limits_{i=1}^{n-1}a_i <a_n$,那么答案是$\sum \limits_{i=1}^{n-1}a_i$。
- 否则,答案是$\frac{1}{2}\sum \limits_{i=1}^{n}a_i$。
当$k>2$,我们以此类推,是否能够得到如下结论呢?
- 如果$\frac{1}{k-1}\sum \limits_{i=1}^{n-1}a_i <a_n$,那么答案是$\frac{1}{k-1}\sum \limits_{i=1}^{n-1}a_i$。
- 否则,答案是$\frac{1}{k}\sum \limits_{i=1}^{n}a_i$。
根据上述安排的方案容易发现第二种情况是正确的。
但是第一种情况有问题:我们不能够假定前$n-1$节电池就一定能安排满$k-1$个位置。
如何判断前$n-1$节电池是否能安排满$k-1$个位置呢?我们发现这就变成了原问题的子问题,所以递归处理即可。
此时的答案一定小于$a_n$,从而第$n$节电池就变成了一个“占位电池”,只需要让它在某个电池位上一直使用就可以了。
同时,注意到“前$n-m$节电池能否安排满$k-m$”个位置对于$m$具有单调性。
也就是说存在某个$m_0$,使得比它小的所有$m$全都能安排满,比它大的所有$m$全都安排不满。
所以我们可以直接二分这个$m_0$的位置,然后检查$\frac{1}{k- m_{0} }\sum \limits_{i=1}^{n- m_{0}}a_i$ 与$a_{n- m_{0} +1}$的大小关系就可以了。
算法本身的复杂度可以做到$O(n)$,瓶颈在于输入以及前缀和。
在考场上,这道题目的数据范围是$n\leq 1000$,导致我一直在想$dp$做法,但是无功而返。
同时我也没有手算样例,而是一直在思考一些非常抽象的东西,导致我没有发现题目的本质。
最后,我之前见过这道题在$k=2$时的题目,但没有听讲解,也没有深入去想,导致我考场上见到这道题目可以说是大脑一片空白。
从中不难发现我个人在解决算法题目上存在的一些弱点:
- 过于依赖数据范围思考解法,难以从题目本身入手。
- 过于高估自己的抽象思维能力,不想或者不屑于分析样例。
- 懒于思考,不能把每个遇见的问题理解清楚。
归根到底还是骄傲轻敌:以为用自己算法竞赛的功底可以轻松水过这门课,所以就抱着一种无所谓的心态去学习和考试,导致这学期在计概上几乎什么也没学到,考的也非常不好,可以说是十分失败了。
这学期的计概课程基本已经结束了,对于这门课来说我也不再有补救的机会,只能寄希望于今后的课程了。
希望在后面的学习中我能始终怀有一个学习者应有的心态,不去过多的考虑成绩和与他人的比较,而将注意力放在学习的内容上。
不只是为其他同学解答问题,向其他同学请教问题也是必不可少的一项学习内容。同学们也没有所谓的“水平高低”之分,每位同学在算法思维方面都可以说有远远超过我的地方,只不过学习的时间太少,才在有些时候没有体现出来应有的实力。
而对我而言,所谓“暂时领先”便沾沾自喜实在是可笑的,停滞不前的水流只会腐烂死亡,唯有奔涌向前才能汇入江海。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号