【转载】利用向量积(叉积)计算三角形的面积和多边形的面积
利用向量积(叉积)计算三角形的面积和多边形的面积:
向量的数量积和向量积:
(1) 向量的数量积
(1) 向量的向量积
两个向量a和b的叉积(向量积)可以被定义为: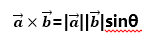
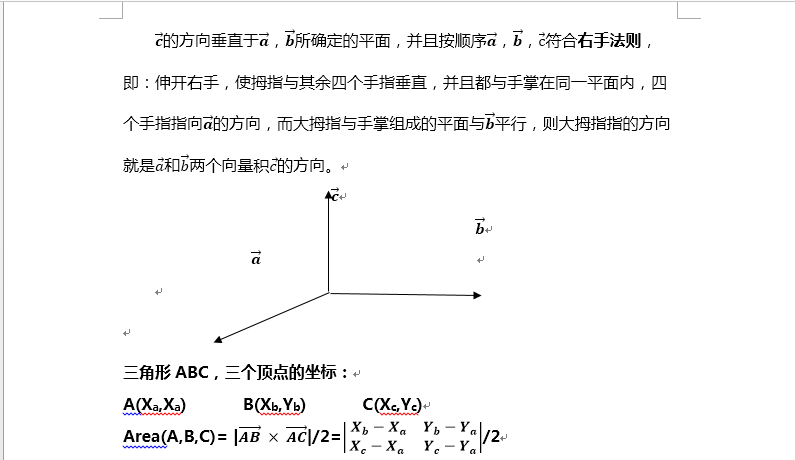
在这里θ表示两向量之间的角夹角(0° ≤ θ ≤ 180°),它位于这两个矢量 所定义的平面上。
向量积的模(长度)![]() 可以解释成以a和b为邻边的平行四边形的面积。求三角形ABC的面积,根据向量积的意义,得到:
可以解释成以a和b为邻边的平行四边形的面积。求三角形ABC的面积,根据向量积的意义,得到: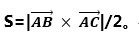
a=axi+ayj+azk;
b=bxi+byj+bzk;
a×b=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k,为了帮助记忆,利用三阶行列式,写成:
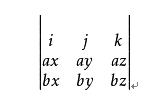
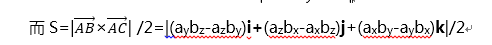

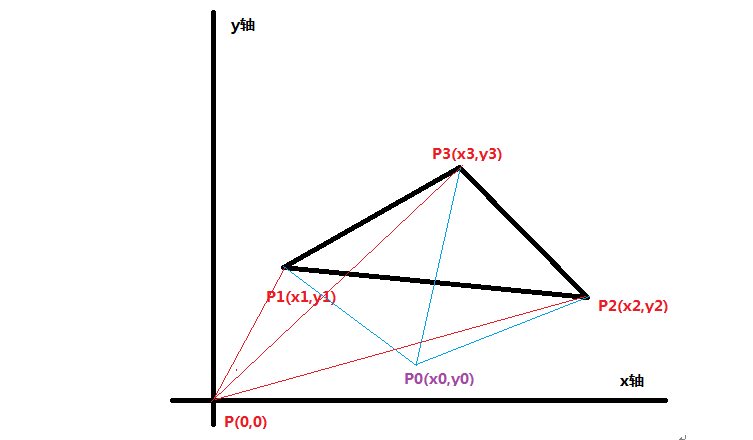
计算任意多边形的面积:(顶点按逆时针顺序排列)
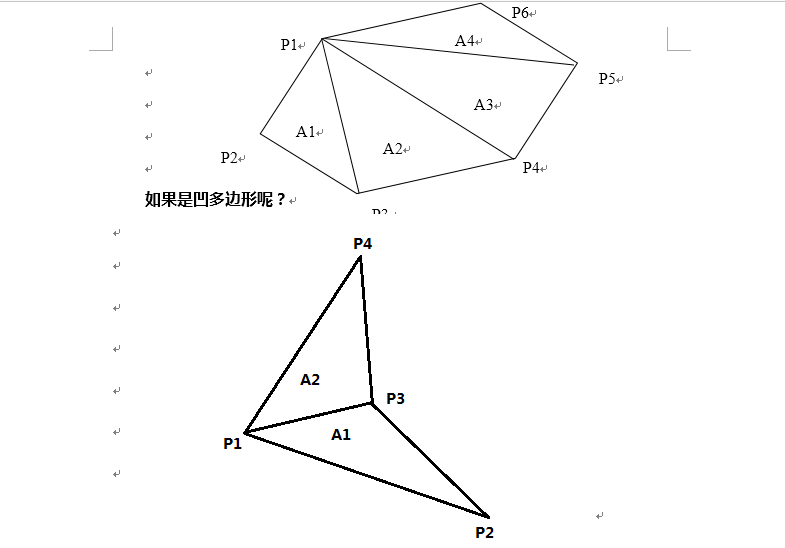
求多边形面积最基础的方法就是用剖分法来做的,就是把多边形分成若干个三角形,然后对每个三角形求面积,求面积,在有精度要求的情况下,不要用海伦-秦九昭公式,海伦公式可能在精度损失方面会比较严重,而且计算量很大。
最适合解决任意多边形面积的方法是:向量积法。
顶点为Pk(k=1,2,3…n)的多边形,其顶点坐标分别为(x1,y1),(x2,y2),(x3,y3)…(xn,yn)。
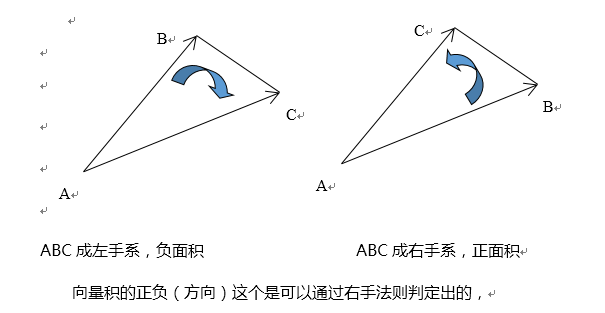
在计算几何里,我们知道,△ABC的面积就是“向量AB”和“向量AC”两个向量叉积的绝对值的一半。其正负表示三角形顶点是在右手系还是左手系。
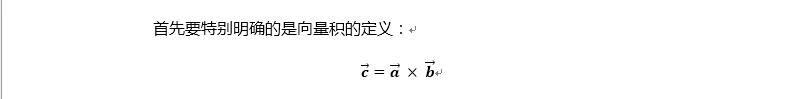







 浙公网安备 33010602011771号
浙公网安备 33010602011771号