【实用性程序】弧微分计算圆周长
最近学了学关于微积分的知识(当然,这还是最简单的),于是想到利用微分进行近似计算圆周长(除以2倍半径就是圆周率pi)
思路:
首先把圆放在直角坐标系中,不妨设圆心(0,0),半径r = 1。 因而,圆的标准方程为 x^2+y^2 = 1 (1)
下面开始微积分大法:(对圆方程这个隐函数求导数)
对方程(1)两边对x求导数: 2*x + 2*y * y′ = 0 (解释一下:x^2 的导数为 2x , y^2 的导数为 2y * y′ , y′就是y对x的导数 , 右边常数1的导数为 0)
解出 y' = - x/y
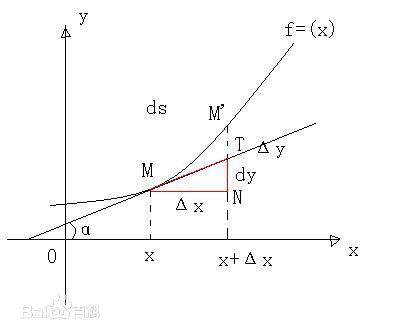
根据微分 : dy = y' * dx , 再由弧微分的计算公式(实际上就是勾股定理), dx 对应的弧长约为 √dx^2+dy^2 . 图中MM' 近似用MT 表示。
然后让dx取一个趋近于0的数,一段一段求和即可(类似割圆法的思想)
代码:
#include<bits/stdc++.h>
using namespace std;
double dx = 1,sum = 0,x,y,dy;
int main()
{
int n;
cin >> n; //精确程度
for (int i = 1 ; i <= n ; i ++) {
sum = 0; dx *= 0.1;
printf("delta x = %llf ... sum = ",dx);
for (x = dx ; x <= 1-dx ; x += dx)
{
y = sqrt(1-x*x);
dy = -x/y*dx;
sum += sqrt(dx*dx+dy*dy);
// printf("%.5f %.5f %.5f\n",x,y,sum);
}
sum += 2*sqrt(dx*dx+dy*dy);
printf("%lf\n",sum*4);
}
return 0;
}
实际测试结果:
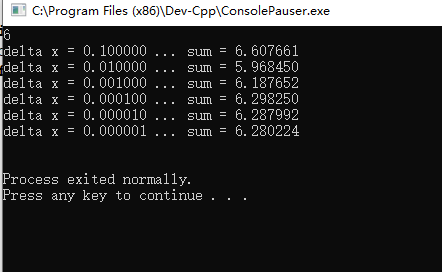
理论结果:
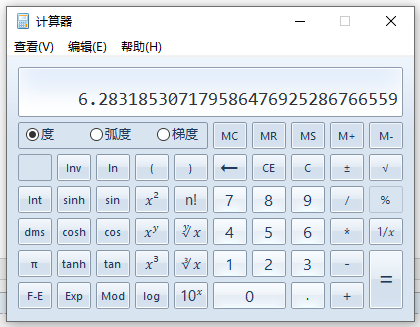


 浙公网安备 33010602011771号
浙公网安备 33010602011771号