【Codeforces】 Round #374 (Div. 2)

Position:http://codeforces.com/contest/721

我的情况

开始还是rank1，秒出C。（11:00机房都走光了，我ma到11:05才走，只打了一个小时）

结果。。。

FST！！尤其是第一题还WA了一发。gi烂。B题还ma得慢。

最后滚到青名。。。。。

反思

首先每次都WA了A题，很不应该，虽然快，样例都没测就交，结果丢了50分。

B题ma得慢。

C题未考虑到LL情况，虽然有上界T，但我没用啊，直接记录到这个点的用了几个点的最短距离，dfs时没有判断与T的关系。统计答案才判，结果FST，WA烂，掉raiting。

D不能怪没时间。很水但没做？问题，人家一个小时也可以AK。我觉得还是分析问题能力要提升，ma代码速度提高，细节要考虑清楚。

官方题解

Round374

A. One-dimensional Japanese Crossword

Recently Adaltik discovered japanese crosswords. Japanese crossword is a picture, represented as a table sized a × b squares, and each square is colored white or black. There are integers to the left of the rows and to the top of the columns, encrypting the corresponding row or column. The number of integers represents how many groups of black squares there are in corresponding row or column, and the integers themselves represents the number of consecutive black squares in corresponding group (you can find more detailed explanation in Wikipedia https://en.wikipedia.org/wiki/Japanese_crossword).

Adaltik decided that the general case of japanese crossword is too complicated and drew a row consisting of n squares (e.g. japanese crossword sized 1 × n), which he wants to encrypt in the same way as in japanese crossword.

$\text{[math]}$ The example of encrypting of a single row of japanese crossword.

Help Adaltik find the numbers encrypting the row he drew.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 100) — the length of the row. The second line of the input contains a single string consisting of n characters 'B' or 'W', ('B' corresponds to black square, 'W' — to white square in the row that Adaltik drew).

Output

The first line should contain a single integer k — the number of integers encrypting the row, e.g. the number of groups of black squares in the row.

The second line should contain k integers, encrypting the row, e.g. corresponding to sizes of groups of consecutive black squares in the order from left to right.

input
3
BBW
output
1
2
input
13
WBBBBWWBWBBBW
output
3
4 1 3 

Note

The last sample case correspond to the picture in the statement.

Understanding

求一个字符串中连续一段B出现的个数，并输出每段的数目

Solution

模拟？枚举→CF官方implementation(翻译:贯彻实施扫一遍→运用吧)。O(n)将字符串扫一遍，如果发现一个'B'，往后找'B'，记录个数即可

Introspection

A题wa了一发，50分啊，raiting啊。

以后一定要测样例，并且考虑到各种特殊的情况，n=1，极限数据爆LL

下次拿小号开黑。。。只要不skip就行。

Code

// <A.cpp> - Fri Sep 30 22:03:52 2016
// This file is made by YJinpeng，created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long long LL;
const int MAXN=110;
inline LL gi() {
    register LL w=0,q=0;register char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')q=1,ch=getchar();
    while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
    return q?-w:w;
}
char s[MAXN];int a[MAXN];
int main()
{
    freopen("A.in","r",stdin);
    freopen("A.out","w",stdout);
    int n=gi(),k=0;
    scanf("%s",s);
    for(int i=0;i<n;i++)
        if(s[i]=='B'){
            int j=i;k++;
            while(s[j++]=='B')a[k]++;
            i=j-1;
        }
    printf("%d\n",k);
    for(int i=1;i<=k;i++)printf("%d ",a[i]);
    return 0;
}

B. Passwords

Vanya is managed to enter his favourite site Codehorses. Vanya uses n distinct passwords for sites at all, however he can't remember which one exactly he specified during Codehorses registration.

Vanya will enter passwords in order of non-decreasing their lengths, and he will enter passwords of same length in arbitrary order. Just when Vanya will have entered the correct password, he is immediately authorized on the site. Vanya will not enter any password twice.

Entering any passwords takes one second for Vanya. But if Vanya will enter wrong password k times, then he is able to make the next try only 5 seconds after that. Vanya makes each try immediately, that is, at each moment when Vanya is able to enter password, he is doing that.

Determine how many seconds will Vanya need to enter Codehorses in the best case for him (if he spends minimum possible number of second) and in the worst case (if he spends maximum possible amount of seconds).

Input

The first line of the input contains two integers n and k (1 ≤ n, k ≤ 100) — the number of Vanya's passwords and the number of failed tries, after which the access to the site is blocked for 5 seconds.

The next n lines contains passwords, one per line — pairwise distinct non-empty strings consisting of latin letters and digits. Each password length does not exceed 100 characters.

The last line of the input contains the Vanya's Codehorses password. It is guaranteed that the Vanya's Codehorses password is equal to some of his n passwords.

Output

Print two integers — time (in seconds), Vanya needs to be authorized to Codehorses in the best case for him and in the worst case respectively.

input
5 2
cba
abc
bb1
abC
ABC
abc
output
1 15
input
4 100
11
22
1
2
22
output
3 4

Note

Consider the first sample case. As soon as all passwords have the same length, Vanya can enter the right password at the first try as well as at the last try. If he enters it at the first try, he spends exactly 1 second. Thus in the best case the answer is 1. If, at the other hand, he enters it at the last try, he enters another 4 passwords before. He spends 2 seconds to enter first 2 passwords, then he waits 5 seconds as soon as he made 2 wrong tries. Then he spends 2 more seconds to enter 2 wrong passwords, again waits 5 seconds and, finally, enters the correct password spending 1 more second. In summary in the worst case he is able to be authorized in 15 seconds.

Consider the second sample case. There is no way of entering passwords and get the access to the site blocked. As soon as the required password has length of 2, Vanya enters all passwords of length 1 anyway, spending 2 seconds for that. Then, in the best case, he immediately enters the correct password and the answer for the best case is 3, but in the worst case he enters wrong password of length 2 and only then the right one, spending 4 seconds at all.

Understanding

给你很多个输入的密码，并且给你正确的密码（保证输入的中有正确的密码）。求输入顺序使得最少与最多的此时可以得到密码，要求按字符串长度顺序输出。

Solution

贪心。记每个字符串的长度，sort。最小：把长度小的输完，然后再输出+1就行。最大：长度小的输完+长度相等并且不等于密码串的个数+1。

Code

// <B.cpp> - Fri Sep 30 22:03:53 2016
// This file is made by YJinpeng，created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#define MOD 1000000007
#define INF 1e9
#define IN inline
#define RG register
using namespace std;
typedef long long LL;
typedef long double LB;
const int MAXN=110;
const int MAXM=100010;
inline int max(int &x,int &y) {return x>y?x:y;}
inline int min(int &x,int &y) {return x<y?x:y;}
inline LL gi() {
    register LL w=0,q=0;register char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')q=1,ch=getchar();
    while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
    return q?-w:w;
}
char c[MAXN];
struct node{
    char s[MAXN];int l;
    bool operator<(node b)const{return l<b.l;}
    void read(){scanf("%s",s);l=strlen(s);}
    bool pan(){
        for(int i=0;i<l;i++)
            if(s[i]!=c[i])return true;
        return false;
    }
}a[MAXN];
int main()
{
    freopen("B.in","r",stdin);
    freopen("B.out","w",stdout);
    int n=gi(),k=gi();
    for(int i=1;i<=n;i++)a[i].read();
    scanf("%s",c);int i,l=strlen(c),ans=0;
    sort(a+1,a+1+n);
    for(i=1;i<=n;i++){
        if(a[i].l>=l)break;
        ans++;
        if(i%k==0)ans+=5;
    }
    printf("%d ",ans+1);int kk=(i-1)%k;
    for(;i<=n;i++){
        if(a[i].l>l)break;
        if(a[i].pan()){
            ans++;kk++;if(kk%k==0)ans+=5;
        }
    }
    printf("%d",ans+1);
    return 0;
}

C. Journey

Recently Irina arrived to one of the most famous cities of Berland — the Berlatov city. There are n showplaces in the city, numbered from 1 to n, and some of them are connected by one-directional roads. The roads in Berlatov are designed in a way such that there are no cyclic routes between showplaces.

Initially Irina stands at the showplace 1, and the endpoint of her journey is the showplace n. Naturally, Irina wants to visit as much showplaces as she can during her journey. However, Irina's stay in Berlatov is limited and she can't be there for more than T time units.

Help Irina determine how many showplaces she may visit during her journey from showplace 1 to showplace n within a time not exceeding T. It is guaranteed that there is at least one route from showplace 1 to showplace n such that Irina will spend no more than T time units passing it.

Input

The first line of the input contains three integers n, m and T (2 ≤ n ≤ 5000, 1 ≤ m ≤ 5000, 1 ≤ T ≤ 10⁹) — the number of showplaces, the number of roads between them and the time of Irina's stay in Berlatov respectively.

The next m lines describes roads in Berlatov. i-th of them contains 3 integers u_i, v_i, t_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i, 1 ≤ t_i ≤ 10⁹), meaning that there is a road starting from showplace u_i and leading to showplace v_i, and Irina spends t_i time units to pass it. It is guaranteed that the roads do not form cyclic routes.

It is guaranteed, that there is at most one road between each pair of showplaces.

Output

Print the single integer k (2 ≤ k ≤ n) — the maximum number of showplaces that Irina can visit during her journey from showplace 1 to showplace n within time not exceeding T, in the first line.

Print k distinct integers in the second line — indices of showplaces that Irina will visit on her route, in the order of encountering them.

If there are multiple answers, print any of them.

Understanding

给你一个DAG(有向无环图)，求1~n路径中，走过点数最多，且边权和<=T的方案。

Solution

记忆化搜索，f[i][j]记录，第i个点走到n号点经过j的最小边权和。转移：f[i][j]=min{f[son][j-1]+w[edge]}

每次转移用d[i][j]记录它转到的儿子。

Code

// <C.cpp> - Fri Sep 30 22:03:53 2016
// This file is made by YJinpeng，created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#define IN inline
#define RG register
using namespace std;
typedef long long LL;
const int MAXN=5010;
const int MAXM=MAXN<<1;
inline LL gi() {
    register LL w=0,q=0;register char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')q=1,ch=getchar();
    while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
    return q?-w:w;
}
int n,tot,be,T;
int to[MAXM],ne[MAXM],fr[MAXN],W[MAXM];
int f[MAXN][MAXN],d[MAXN][MAXN];bool used[MAXN];
void add(int u,int v,int w){
    to[++tot]=v;ne[tot]=fr[u];fr[u]=tot;W[tot]=w;
}
void dfs(int x){
    if(x==n){f[x][1]=0;return;}
    if(used[x])return;used[x]=true;
    for(int i=fr[x];i;i=ne[i]){
        dfs(to[i]);
        for(int j=1;j<=n;j++){
            if(f[to[i]][j-1]==be)continue;
            if(f[to[i]][j-1]+W[i]>T)continue;//..会爆int
            if(f[to[i]][j-1]+W[i]<f[x][j]){
                f[x][j]=f[to[i]][j-1]+W[i];
                d[x][j]=to[i];
            }
        }
    }
}
int main()
{
    freopen("C.in","r",stdin);
    freopen("C.out","w",stdout);
    n=gi();int m=gi();T=gi();
    for(int i=1;i<=m;i++){
        int u=gi(),v=gi(),w=gi();
        add(u,v,w);
    }
    memset(f,123,sizeof(f));be=f[1][1];
    dfs(1);int i;
    for(i=n;i;i--)
        if(f[1][i]<=T)break;
    printf("%d\n",i);
    for(int o=1;i;i--){
        printf("%d ",o);
        o=d[o][i];
    }
    return 0;
}

D. Maxim and Array

Recently Maxim has found an array of n integers, needed by no one. He immediately come up with idea of changing it: he invented positive integer x and decided to add or subtract it from arbitrary array elements. Formally, by applying single operation Maxim chooses integer i (1 ≤ i ≤ n) and replaces the i-th element of array a_i either with a_i + x or with a_i - x. Please note that the operation may be applied more than once to the same position.

Maxim is a curious minimalis, thus he wants to know what is the minimum value that the product of all array elements (i.e. 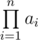$\text{[math]}$ ) can reach, if Maxim would apply no more than k operations to it. Please help him in that.

Input

The first line of the input contains three integers n, k and x (1 ≤ n, k ≤ 200 000, 1 ≤ x ≤ 10⁹) — the number of elements in the array, the maximum number of operations and the number invented by Maxim, respectively.

The second line contains n integers a₁, a₂, ..., a_n (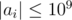 $\text{[math]}$ ) — the elements of the array found by Maxim.

Output

Print n integers b₁, b₂, ..., b_n in the only line — the array elements after applying no more than k operations to the array. In particular, $\text{[math]}$ should stay true for every 1 ≤ i ≤ n, but the product of all array elements should be minimum possible.

If there are multiple answers, print any of them.

input
5 3 1
5 4 3 5 2
output
5 4 3 5 -1
input
5 3 1
5 4 4 5 5
output
5 1 4 5 5

Understanding

给你一列数和k个操作，每次操作要将一个数(+|-)x，舍得最后乘积最小。

Solution

贪心。%遥犇。首先可以想到，使结果为负会很好，如果为正，也要使其尽量小。那么记录为负的个数，开小根堆记录绝对值的最小值，每次修改最小值会是答案更小。

设a×b，a<b，(a+x)×b<a×(b+x)，即证。如果剩下负数为奇数个，+x　else -x。

Code

// <D.cpp> - Fri Sep 30 22:03:53 2016
// This file is made by YJinpeng，created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <queue>
#define IN inline
#define RG register
using namespace std;
typedef long long LL;
const int MAXN=200010;
inline LL gi() {
    register LL w=0,q=0;register char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')q=1,ch=getchar();
    while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
    return q?-w:w;
}
LL a[MAXN];
struct node{LL s;int p;};
priority_queue<node>q;
IN bool operator<(RG node a,RG node b){return a.s>b.s;}
int main()
{
    freopen("D.in","r",stdin);
    freopen("D.out","w",stdout);
    int n=gi(),k=gi(),x=gi(),b=0;
    for(int i=1;i<=n;i++)
        a[i]=gi(),q.push((node){a[i]<0?-a[i]:a[i],i}),b+=a[i]<0;
    while(k--){
        int p=q.top().p;q.pop();b-=a[p]<0;
        if(b&1)a[p]+=x;else a[p]-=x;
        b+=a[p]<0;q.push((node){a[p]<0?-a[p]:a[p],p});
    }
    for(int i=1;i<=n;i++)printf("%lld ",a[i]);
    return 0;
}

posted @ 2016-10-01 21:49 _Mashiro 阅读(723) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

_Mashiro

彩虹的美丽是因为经历了风雨的洗礼，朝阳的光辉是因为冲破了黑夜的束缚

【Codeforces】 Round #374 (Div. 2)

我的情况

反思

官方题解

Understanding

Solution

Introspection

Code

Understanding

Solution

Code

Understanding

Solution

Code

Understanding

Solution

Code

公告