几何建模与处理之五 Bezier曲线与B样条曲线
几何建模与处理之五 Bezier曲线与B样条曲线
Bezier曲线
建模的两种形式:
- 重建(Reconstruction)
- 逆向工程:形状已有,要将其“猜”出来
- 采样->拟合:需要函数空间足够丰富(表达能力够)
- 代数观点:{a,b,c}作为基函数的组合权系数
- 设计(Design)
- 自由设计:凭空产生,或从一个简单的形状编辑得到
- 交互式编辑:几何直观性要好
- 几何观点:基函数{t2,t,1}作为控制点的组合权系数
二次多项式曲线(抛物线):
使用幂基表示曲线
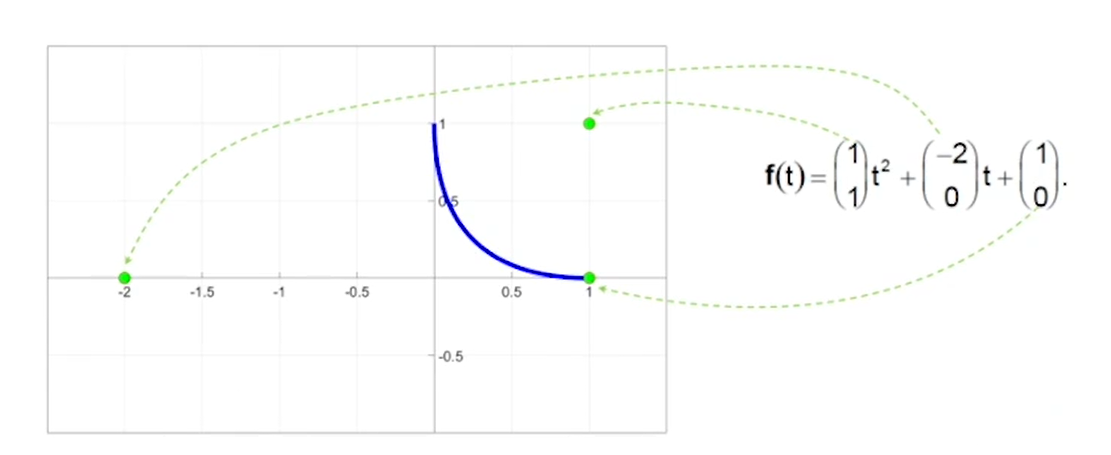
使用Bernstein基函数表达
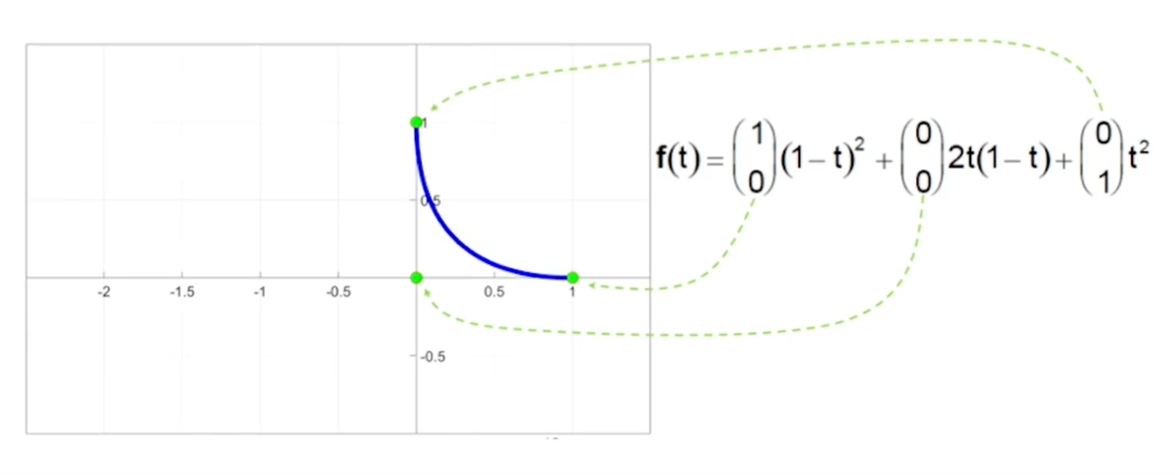
系数顶点与曲线关联性强,具有很好的几何意义,对于交互式曲线设计更直观.
Bernstein基函数
n次Bernstein基函数:\(B=({B_0^{(n)}, B_1^{(n)},...,B_n^{(n)}})\)
性质:
-
对称性:\(B_i^n(t)=B_{n-1}^n(1-t)\)
-
\(B_i^{(n)}\)在\(t=\frac{i}{n}\)达到最大值
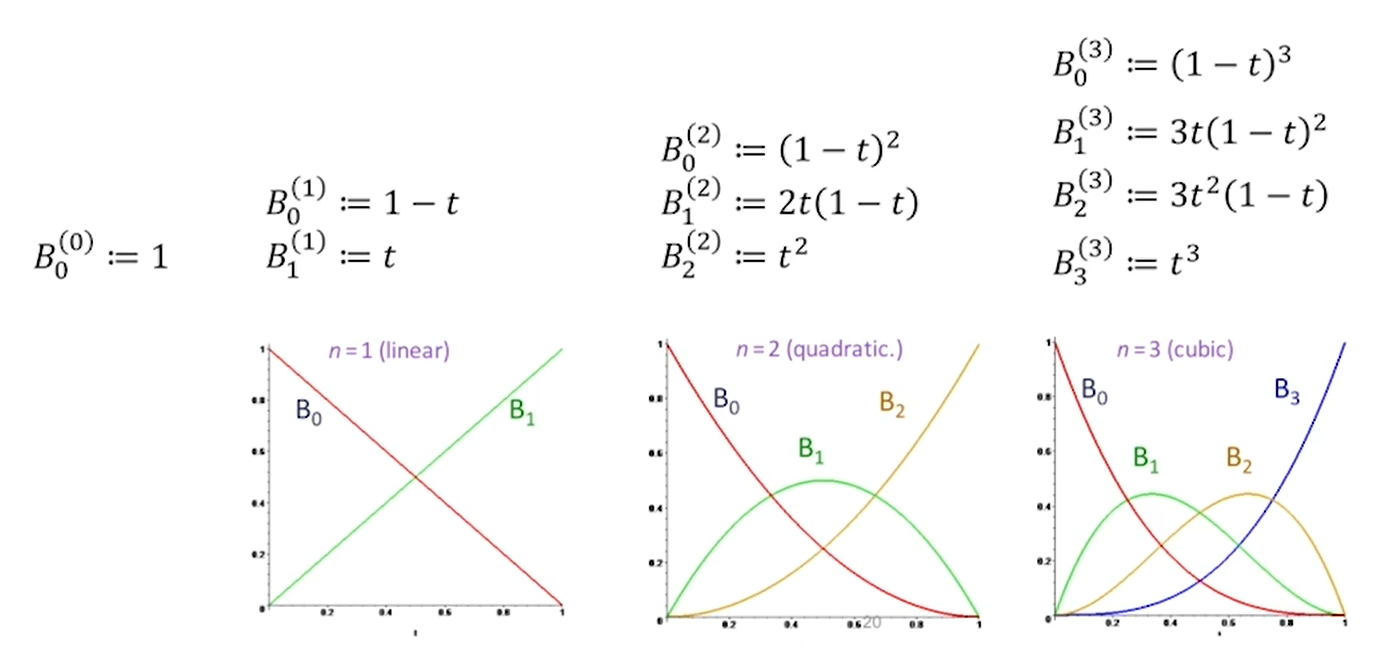
用Bernstein基函数所表达的曲线具有非常好的几何意义
Bezier曲线
n次Berzier曲线:n+1个控制点
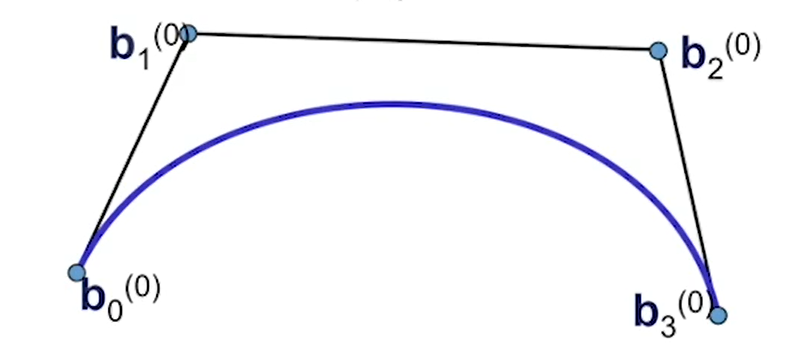
Berzier曲线的性质来源于Bernstein基函数的性质。
Bernstein基函数与Bezier曲线的性质
-
正权性:正性+权性
- \(B_i^{(n)}(t) \ge 0,t\in [0,1]\)
- \(\sum_{i=1}^n B_i^{(n)}(t) = 1,t\in [0,1]\)
-
基性:B是次数不高于n的多项式集合(空间)的一组基
-
递推公式:
- 基函数的递推公式:\(B_i^{(n)}(t)=(1-t)B_i^{(n-1)}(t)+tB_{i-1}^{(n-1)}(t) \quad B_0^0(t)=1,B_i^{(n)}(t)=0\quad for\quad i\notin{0...n}\)
- 高阶的基函数由两个低阶的基函数“升阶”得到,利于保持一些良好的性质
-
端点插值性:Bezier曲线经过首位两个控制顶点
-
导数:
- \(f'(t)=n\sum_{i=0}^{n-1}B_i^{n-1}(t)(p_{i+1}-p_i)\)
- \(f^{[r]}(t)=\frac{n!}{(n-r)!}\sum_{i=0}^{n-r}B_i^{n-r}(t)· \Delta ^rp_i\)
Bezier曲线的端点性质
- 端点插值:
- 端点的切线方向与边相同
- 端点的2阶(k)切线与3点(k+1)相关
-
升阶:\((1-t)B_i^n(t)=(1-\frac{i}{n+1})B_i^{n+1}(t)\) => \(tB_i^n(t)=\frac{i+1}{n+1}B_i^{n+1}(t)\)
Bezier曲线升阶:$$f(t)=\sum_{i=0}{n+1}B_i(t)[\frac {n+1-i}{n+1}P_i+\frac{i}{n+1}P_{i-1}]$$
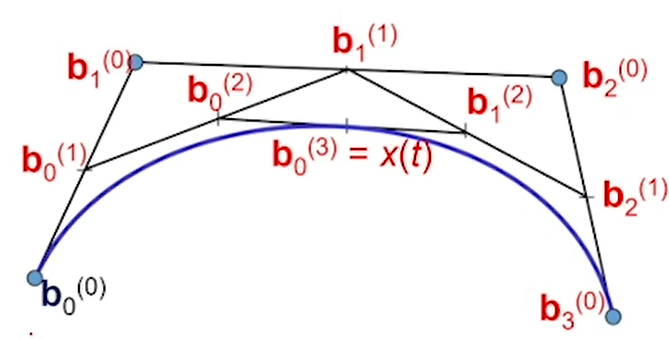
De casteljau algorithm
根据基函数的递推公式:\(B_i^{(n)}(t)=(1-t)B_i^{(n-1)}(t)+tB_{i-1}^{(n-1)}(t)\)
给定一个t,就能求出x(t):\(b_i^{(r)}=(1-n)b_i^{r-1}+tb_{i+1}^{(r-1)}\)
几何样条曲线
两Bezier曲线的拼接条件:
C0:
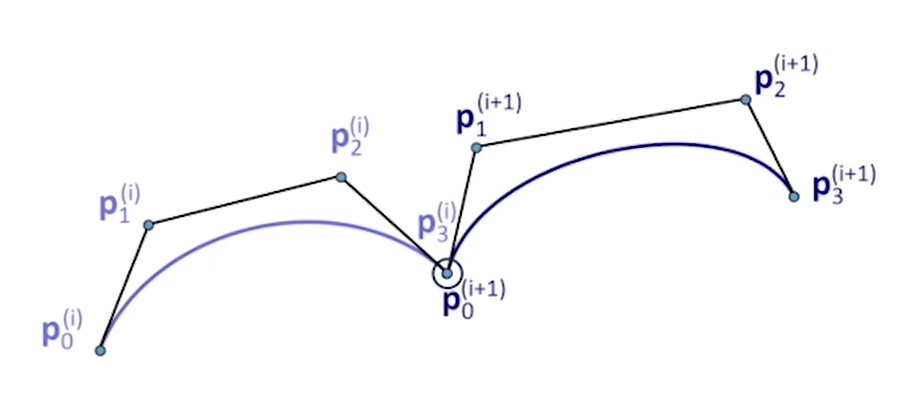
G1:三点共线
C1:三点共线且等长
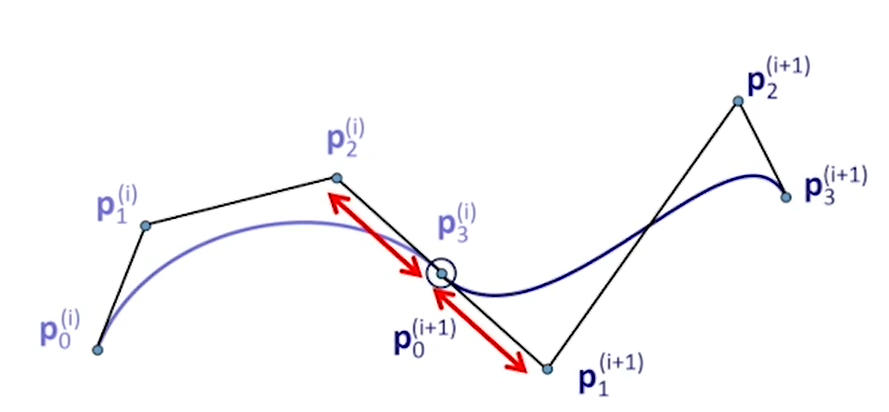
C2:\(d^2/dt^2\)为\((p_2-2p_1+p_0),(p_n-2p_{n-1}+p_{n-2})\),阴影三角形相似
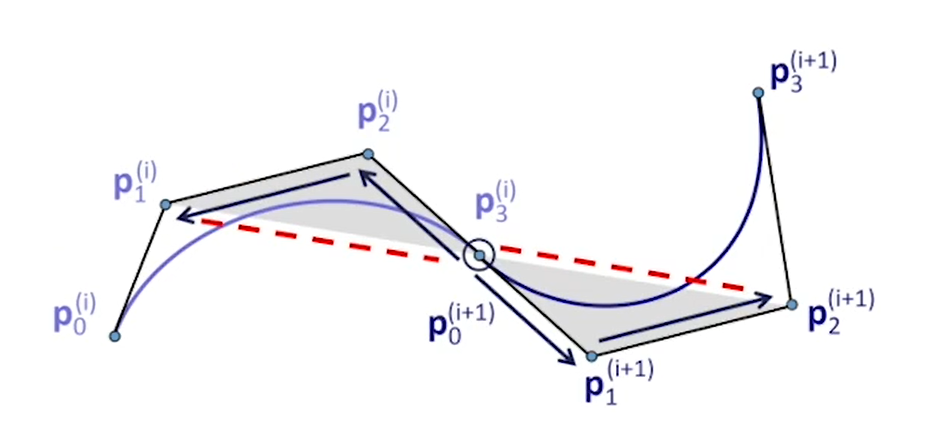
构造3次插值Bezier曲线的几何方法
工程中,在点pi(0<i<n)处,作pi-1和pi+1连线的平行线,取1/6的位置作为控制点。一段曲线由四个点约束。
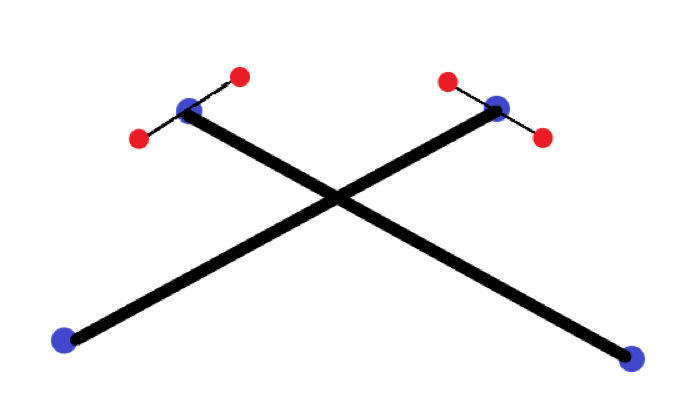
B样条
Bezier曲线(Bernstein基函数)存在全局性,不利于设计。
B样条曲线:分段Bezier曲线,具有局部性。
样条曲线的统一表达
基函数
均匀结点(Uniform)
非均匀结点(\(t_0<t_1<....<t_n<...t_{n+k}\))
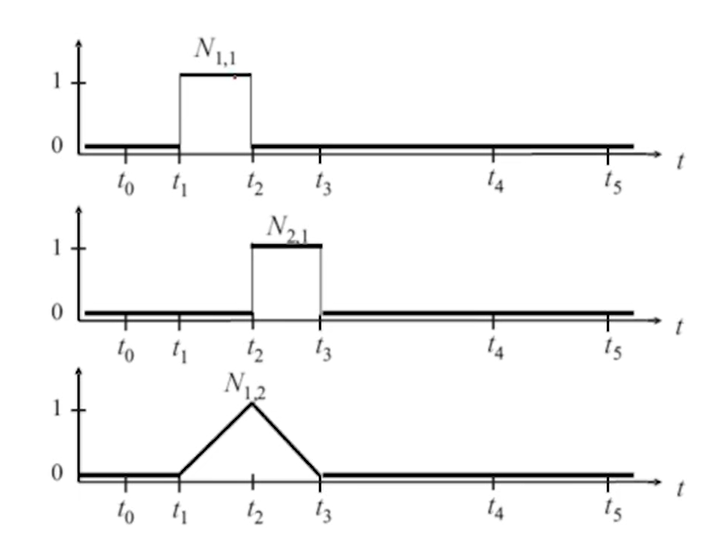
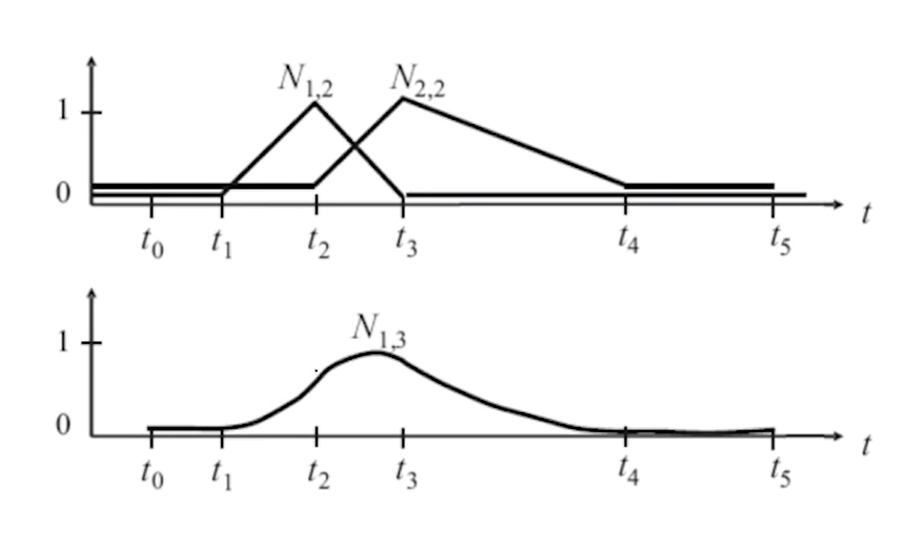
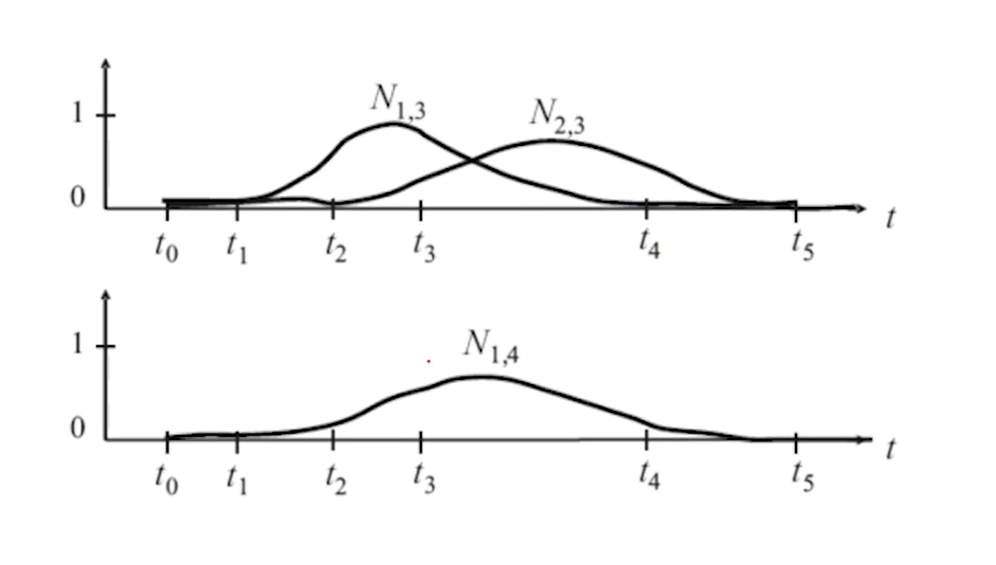
性质:
- \(N_{i,k}(t)>0\) for \(t_i<t<t_{i+k}\)(局部性)
- \(\sum_{i=0}^nN_{i,k}(t)=1\) for \(t_{k-1}\le t \le t_{n+1}\) (权性)
- \(N_{i,k}(t)\)在\(t_j\)处是Ck-2
B-spline curve
给定n+1个控制点,\(d_0,...d_n\in R^3\),\(T=(t_0,...t_{n+k})\)称为向量节点。
每多出一个重结点(Multiple knots),曲线的光滑性降一阶。
例如,k=4,n=5的B-spline curve
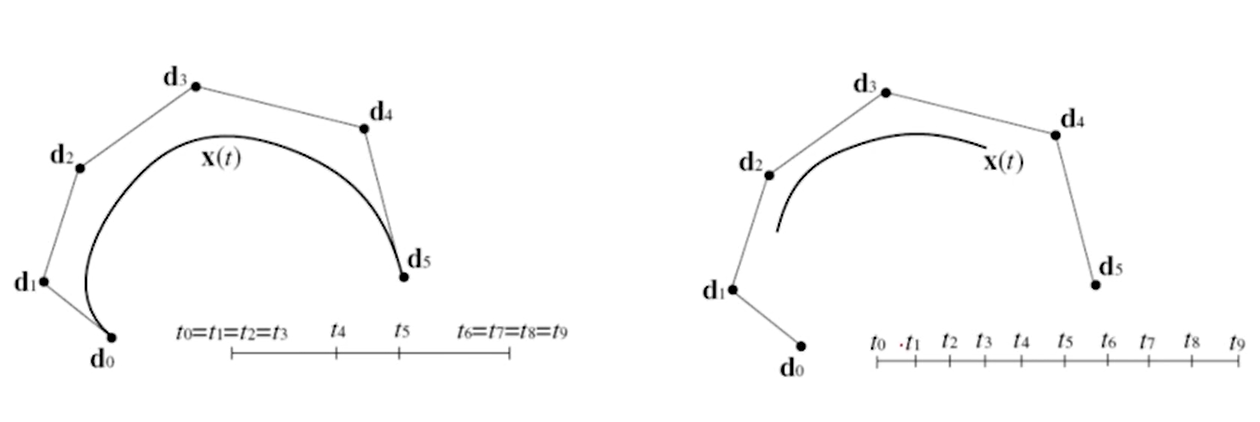
k重时(0,...,0,1,...,1)为Bernstein基。
The de Boor algorithm
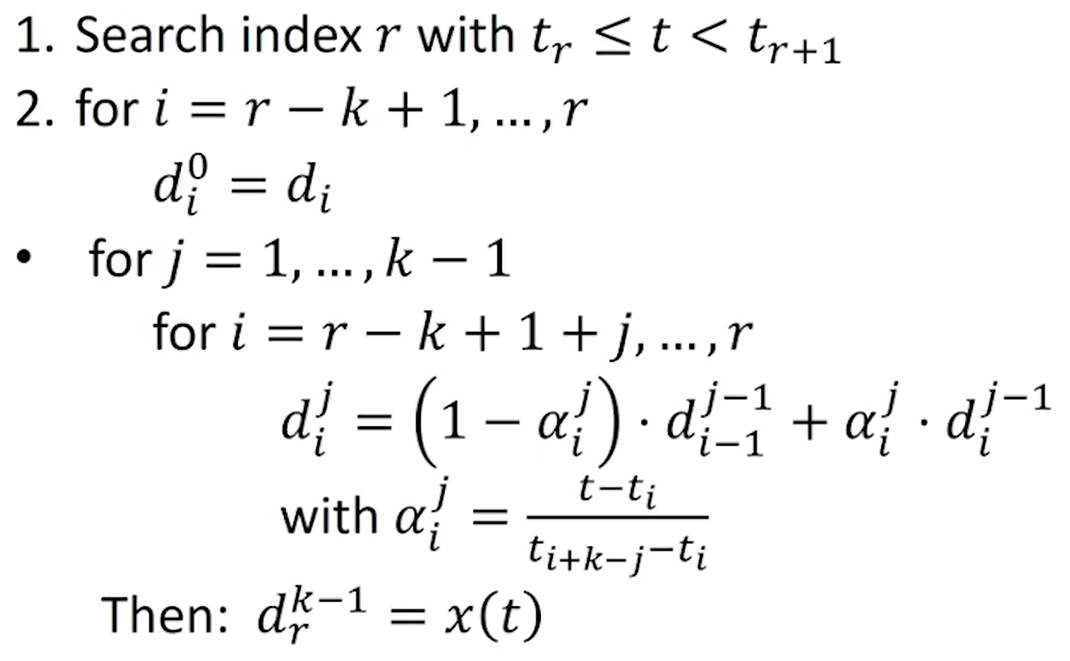


 浙公网安备 33010602011771号
浙公网安备 33010602011771号