几何建模与处理之三 参数曲线

几何建模与处理之三 参数曲线

目录

• 几何建模与处理之三 参数曲线
  • 多元函数
    • 张量积
    • 多元函数的神经网络表达
  • 向量值函数
    • • 平面参数曲线
      • 空间参数曲线
      • 参数曲面
      • 二维映射
      • 三维映射
      • 降维映射（低维映射）
      • 一般映射
  • 曲线拟合
    • 曲线拟合问题
    • 参数化问题
    • 曲面参数化

在前两节中，学习了一元（单变量）函数\(f:R^1\to R^1\quad y=f(x)\)的数据拟合方法。接下下学习多元函数及多元函数的数据拟合。

多元函数

多元，即多变量，函数形式如下：

\[f:R^n\to R^1\quad \begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\to y\\y=f(x_1,x_2,\dots,x_n) \]

多元函数的基函数构造需要引入张量积的概念。

张量积

定义：多个一元基函数的乘积形式

优点：定义简单

不足：随着维数增加，基函数个数急剧增加，导致变量技据增加（求解系统规模急剧增加，求解代价大）

二元函数的基函数：即用两个一元函数的基函数的相互乘积来定义

例： 二次二元多项式函数\(z=f(x,y)\)的基函数\(\lbrace 1,x,y,x^2,xy,y^2\rbrace\)

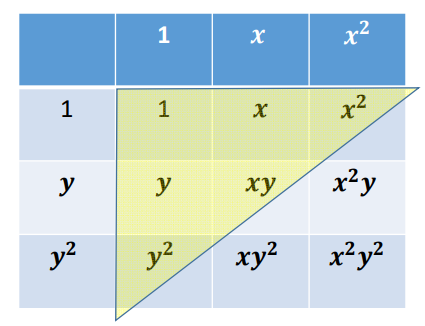
张量积基函数：

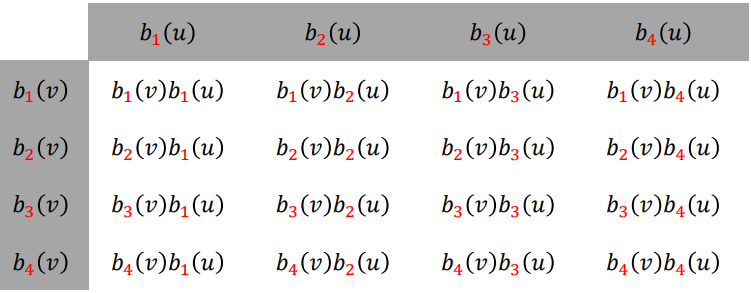
多元函数的神经网络表达

用一个单变量函数\(\sigma(x)\)（激活函数）的不同仿射变换构造“基函数”：基函数数目可控

\[y=f(x_1,x_2,\dots,x_n)=\omega_0+\sum_{j=1}^mw_i\sigma(a_j^1x_1+\dots+a_j^ix_i+\dots+a_j^nx_n+b_j) \]

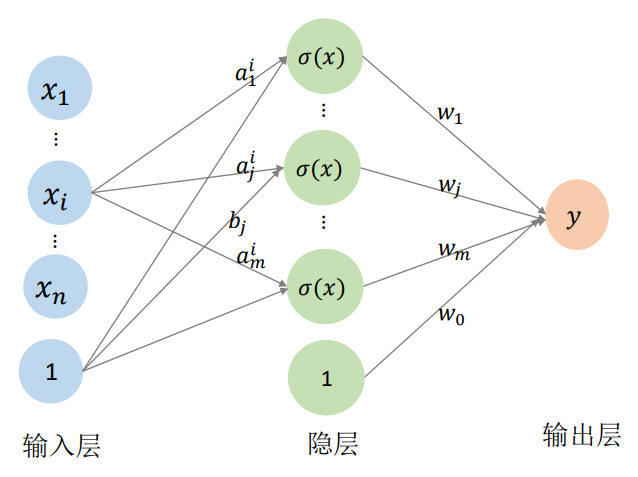
向量值函数

向量值，即多个应变量

单变量向量值函数：

\[f:R^1\to R^m\quad x\to\begin{pmatrix}y_1\\\vdots\\y_n\end{pmatrix}\\\begin {cases}y_1=f_1(x)\\\vdots\\y_m=f_m(x)\end{cases} \]

看成多个单变量函数，各个函数独立无关

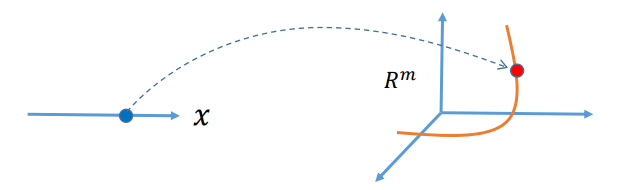
几何解释：

一个实数\(x\in R^1\)映射到\(m\)维空间\(R^m\)的一个点，轨迹构成\(R^m\)的一条“曲线”，本质维度为1

平面参数曲线

函数形式：

\[f:R^1 \to R^2\quad \begin {cases}x=x(t)&t\in [0,1]\\y=y(t)&t\in [0,1]\end {cases} \]

几何解释：

一条曲线由一个变量参数𝑡决定，也称为单参数曲线，参数𝑡可看成该曲线的“时间”变量，可灵活表达非函数型的曲线（任意曲线）。

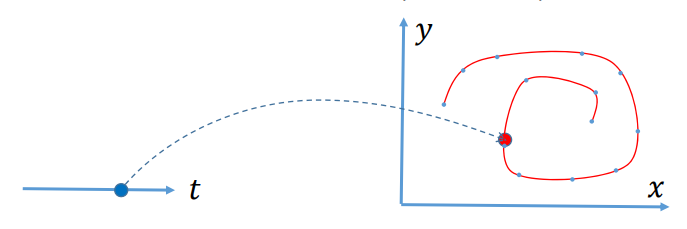
空间参数曲线

函数形式：

\[f:R^1 \to R^3\quad \begin {cases}x=x(t)\\y=y(t)&t\in [0,1]\\z=z(t)\end {cases} \]

几何解释：

一条曲线由一个变量参数𝑡决定，也称为单参数曲线，参数 𝑡可看成该曲线的“时间”变量，可灵活表达非函数型的曲线（任意曲线）。

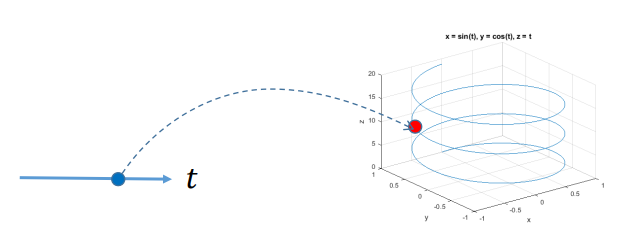
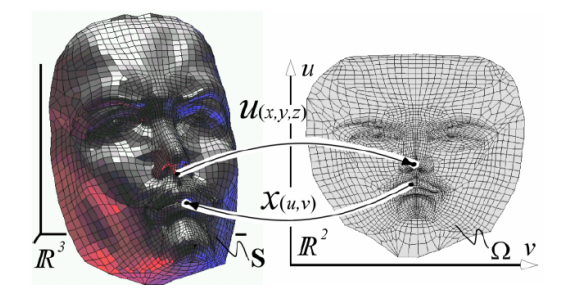
参数曲面

\[f:R^2 \to R^3\quad \begin {cases}x=x(u,v)\\y=y(u,v)&(u,v)\in [0,1]×[0,1]\\z=z(u,v)\end {cases} \]

几何解释：

一张曲面由两个参数ሺ𝑢, 𝑣ሻ决定，也称为双参数曲面， 可灵活表达非函数型的任意曲面。

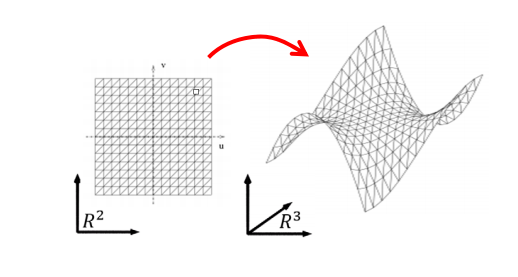
二维映射

\[f:R^2 \to R^2\quad \begin {cases}x=x(u,v)\\y=y(u,v)\end {cases}(u,v)\in [0,1]×[0,1]\\ \]

几何解释：

二维区域之间的映射，可看成特殊的曲面（第三个维度始终为 0 ）

应用：图像变形

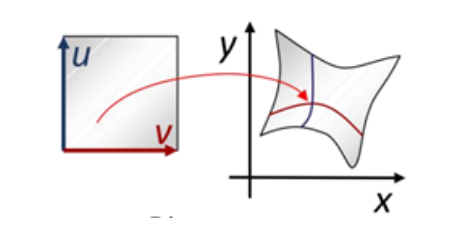
三维映射

\[f:R^3 \to R^3\quad \begin {cases}x=x(u,v,w)\\y=y(u,v,w)\\z=z(u,v,w)\end {cases}(u,v,w)\in [0,1]^3\\ \]

几何解释：

三维体区域之间的映射

应用：体形变、体参数化

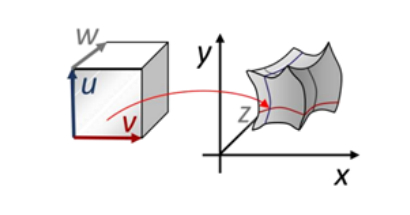
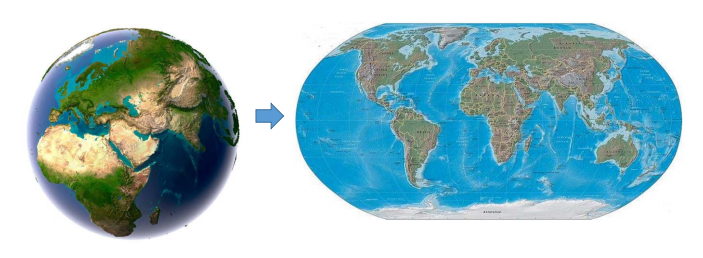
降维映射（低维映射）

\[f:R^3\to R^2 \]

降维映射一般有信息丢失，丢失的信息大部分情况下不可逆，即无法恢复

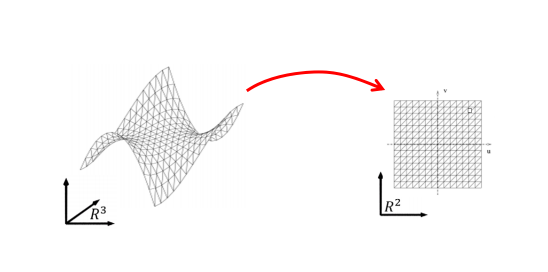
一般映射

\[f:R^n\to R^m \]

如果\(n\lt m\)，为低维到高维的映射（高维的超曲面，n维流形曲面），本征维度为n。如果\(n\lt m\)，为降维映射，一般信息有损失， 如果\(R^n\)中的点集刚好位于一个𝑚 维（或小于𝑚 ）的流形上，则映射可能是无损的，即可以被恢复的。

曲线拟合

曲线拟合问题

输入：给定平面上系列点\((x_i,y_i),i=1,2,\dots,n\)

输出：一条参数曲线，拟合这些点

\[f:R^1\to R^2\quad \begin{cases}x=x(t)\\y=y(t)\end{cases}t\in [0,1] \]

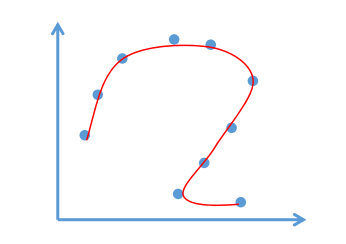
问题：对数据点\((x_i,y_i)\)，对应哪个参数\(t_i\)?

误差度量：\(E=\sum_{i=1}^n \begin{Vmatrix} \begin{pmatrix}x(t_i)\\y(t_i)\end{pmatrix}-\begin{pmatrix}x_i\\y_i\end{pmatrix}\end{Vmatrix}^2=\begin{Vmatrix} \mathbf p(t_i)-\mathbf p_i\end{Vmatrix}^2\) \(\mathbf p=\mathbf p(t)=\begin{pmatrix}x(t)\\y(t)\end{pmatrix}\)

参数化问题

求数据点所对应的参数：一个降维的问题！

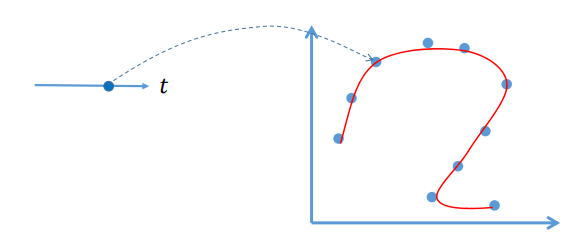
点列的参数化方法

• Equidistant (uniform) parameterization 均匀参数化

\(t_{i+1}-t_i=const\)

\(e.g.t_i=i\)

Geometry of the data points is not considered
不考虑数据点的几何形状。

• Chordal parameterization 弦长参数化

\(t_{i+1}-t_i=\begin{Vmatrix} k_{i+1}-k_i\end{Vmatrix}\)

Parameter intervals proportional to the distances ofneighbored control points
参数间隔与相邻控制点的距离成正比

• Centripetal parameterization 向心参数化

  \(t_{i+1}-t_i=\sqrt{\begin{Vmatrix} k_{i+1}-k_i\end{Vmatrix}}\)

• Foley parameterization Foley参数化

  lnvolvement of angles in the control polygon
  控制多边形中角的变化

  \(t_{t+1}-t_i=\begin{Vmatrix} k_{i+1}-k_i\end{Vmatrix}·(1+\frac32\frac{\hat a_i\begin{Vmatrix} k_{i}-k_{i-1}\end{Vmatrix}}{\begin{Vmatrix} k_{i}-k_{i-1}\end{Vmatrix}+\begin{Vmatrix} k_{i+1}-k_i\end{Vmatrix}}+\frac32\frac{\hat a_{i+1}\begin{Vmatrix} k_{i+1}-k_{i}\end{Vmatrix}}{\begin{Vmatrix} k_{i+1}-k_{i}\end{Vmatrix}+\begin{Vmatrix} k_{i+2}-k_{i+1}\end{Vmatrix}})\)

  \(\hat a_i=\min(\pi-a_i,\frac\pi 2)\)

  \(a_i=\angle(k_{i-1},k_i,k_{i+1})\)

曲面参数化

三维的点找二维的参数：一个降维的问题

后续再学习