DirectX11——粒子系统
DirectX11 粒子系统
前言
粒子系统表示三维计算机图形学中模拟一些特定的模糊现象的技术,而这些现象用其它传统的渲染技术难以实现真实感的物理运动规律。(百度百科)
我们经常使用粒子系统来模拟火焰、爆炸、烟雾等现象,在Unity3D中就有一套成熟粒子系统以供游戏开发者使用。最近在学习使用DirectX11中的着色器反射来构建粒子系统渲染框架,并尝试使用这一套框架实现爆炸和喷泉特效。
本人学习的DirectX11是基于Windows SDK实现的,本次粒子系统的所有前置知识以及粒子系统的实现均来自DirectX11 with Windows SDK教程:https://www.cnblogs.com/X-Jun/p/9028764.html
本次粒子系统的框架也使用了https://github.com/MKXJun/DirectX11-With-Windows-SDK中第35个项目中的ParticleEffect框架和ParticleRender。
涵盖知识
粒子系统的实现属于教程中高级部分的内容,需要的知识比较全面,具体请看思维导图:
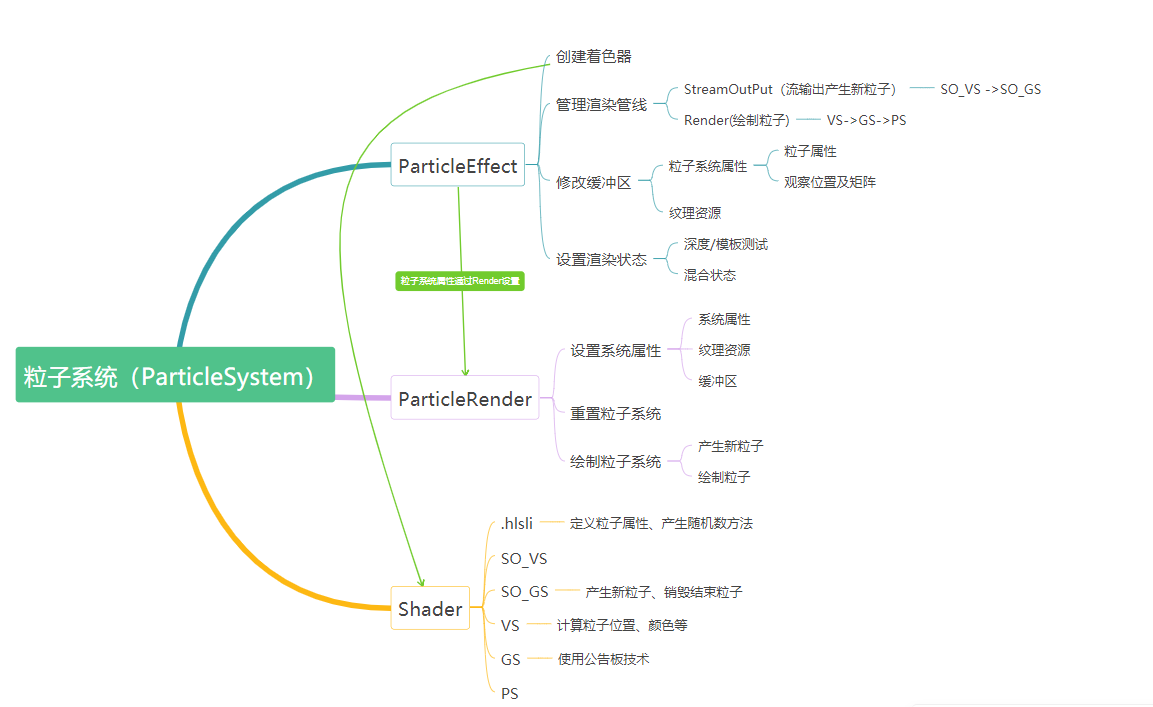
总结一下:着色器的书写与C++中创建着色器、流输出阶段、利用着色器反射修改缓冲区数据、混合状态和深度/模板测试、利用几何着色器实现公告板效果。
通过粒子系统的实现学习,可以学习到:
-
利用几何着色器和流输出阶段高效产生和储存粒子
-
使用物理知识来模拟物理运动规律
-
锻炼设计渲染框架的能力
粒子系统
粒子系统需要较多的属性,不同的粒子系统会拥有不同的属性,在通用的粒子系统中,我们定义以下属性:
1、发射位置
2、发射方向
3、发射间隔
4、粒子存活时间
5、系统时长
6、系统步长
7、最大粒子数目
8、观察位置和观察矩阵
这些属性应该不难理解,观察位置和观察矩阵在其他渲染系统中也是必备的。
粒子
粒子本身也有不少的属性,通用的粒子属性如下:
struct ParticleVertex { XMFLOAT3 initialPos; // 初始位置 XMFLOAT3 initialVel; // 初始速度 XMFLOAT3 size; // 粒子大小 float age; // 粒子年龄 uint type; // 粒子类型 }
粒子类型包括发射器粒子和普通发射粒子,发射器粒子会根据自身年龄(解释为年龄不太合适,因为它会不断地循环置零)来判断是否发射新粒子,发射新粒子后重新积累时间,又一次达到系统的发射间隔时发射新粒子。在几何着色器中,发射粒子总是被输出到顶点缓冲区,如果没控制好粒子最大数量、粒子发射间隔和粒子存活时间,缓冲区无法发容纳射器粒子,粒子系统就会消失(没有粒子)。
随机数值
我们可以在C++使用random来产生随机数,但在HLSL中并没有产生随机数的方法,因此我们需要自己定义一些产生随机数的方法。通常情况下,对一个Texture1D资源进行不同位置的采样可以达到获得随机数的效果。创建一个1D纹理,里面每个元素是float4(DXGI_FORMAT_R32G32B32A32_FLOAT),然后我们使用区间[-1, 1]的随机4D向量来填满纹理,采样的时候则使用wrap寻址模式即可。采样的结果也是在[-1, 1],可根据需要通过计算使之落在指定范围。
下面是获得随机单位向量的方法:
float3 RandUnitVec3(float offset) { // 使用游戏时间加上偏移值来从随机纹理采样 float u = (g_GameTime + offset); // 分量均在[-1,1] float3 v = g_RandomVecMap.SampleLevel(g_SamLinear, u, 0).xyz; // 标准化向量 return normalize(v); }
接下来的爆炸和喷泉特效的简单模拟,在这里只讲解主要的步骤。
喷泉
喷泉系统:粒子从某个点产生,并沿着圆锥体范围内的随机方向向上发射,最终重力会使得它们掉落到地面。
重力的模拟比较简单,在Fountain.hlsli中定义重力加速度G,在计算粒子位置时使用物理匀加速直线运动位移公式:x = 1/2 * a * t * t + v * t计算位移,加上初始位置即可。
// Fountain.hlsli ... cbuffer CBFixed : register(b1) { // 重力加速度 float3 g_G = float3(0.0f, -9.8f, 0.0f); // 纹理坐标 float2 g_QuadTex[4] = { float2(0.0f, 1.0f), float2(1.0f, 1.0f), float2(0.0f, 0.0f), float2(1.0f, 0.0f) }; } ... // Fountain_VS.hlsl VertexOut VS(VertexParticle vIn) { VertexOut vOut; float t = vIn.Age; // 恒定加速度等式 vOut.PosW = 0.5f * t * t * g_G + t * vIn.InitialVelW + vIn.InitialPosW; // 颜色随着时间褪去 float opacity = 1.0f - smoothstep(0.0f, 1.0f, t / 1.0f); vOut.Color = float4(1.0f, 1.0f, 1.0f, opacity); vOut.SizeW = vIn.SizeW; vOut.Type = vIn.Type; return vOut; }
在随机数部分已经提及,我们定义了产生随机单位向量的方法:
float3 RandUnitVec3(float offset) { // 使用游戏时间加上偏移值来从随机纹理采样 float u = (g_GameTime + offset); // 分量均在[-1,1] float3 v = g_RandomVecMap.SampleLevel(g_SamLinear, u, 0).xyz; // 标准化向量 return normalize(v); }
在产生新粒子我们可以使用以下计算使向量集中在圆锥区域:
float3 vRandom = RandUnitVec3(offset); vRandom.x *= 0.5f; // 可根据圆锥的范围乘上特定值使向量集中在指定区域 vRandom.z *= 0.5f; vRandom.y = sqrt(1 - vRandom.x * vRandom.x - vRandom.z * vRandom.z); // 落在单位圆上
在模拟喷泉中发现,一帧发射一个粒子的效果仍然很差,需要使用循环来产生更多的粒子。
注意:几何着色器的每次调用最多只能处理1024个标量
// Fountain_SO_GS.hlsl #include " Fountain.hlsli" [maxvertexcount(4)] void GS(point VertexParticle gIn[1], inout PointStream<VertexParticle> output) { gIn[0].Age += g_TimeStep; if (gIn[0].Type == PT_EMITTER) { // 是否到时间发射新的粒子 if (gIn[0].Age > g_EmitInterval) { // for循环产生更多粒子,以三个粒子为例 for (int i = 0; i < 3; i++) { float3 vRandom = RandUnitVec3(g_GameTime * i); // 不同的偏移量进行采集 vRandom.x *= 0.5f; // 可根据圆锥的范围乘上特定值使向量集中在指定区域 vRandom.z *= 0.5f; vRandom.y = sqrt(1 - vRandom.x * vRandom.x - vRandom.z * vRandom.z);// 落在单位圆上 VertexParticle p; p.InitialPosW = g_EmitPosW.xyz; p.InitialVelW = 4.0f * vRandom; p.SizeW = float2(3.0f, 3.0f); p.Age = 0.0f; p.Type = PT_FLARE; output.Append(p); } // 重置时间准备下一次发射 gIn[0].Age = 0.0f; } // 总是保留发射器 output.Append(gIn[0]); } else { // 用于限制粒子数目产生的特定条件,对于不同的粒子系统限制也有所变化 if (gIn[0].Age <= g_AliveTime) output.Append(gIn[0]); } }
爆炸
发射器粒子产生N个随机方向的外壳粒子。在经过一个短暂时间后,每个外壳粒子应当爆炸产生M个粒子。每个外壳不需要在同一个时间发生爆炸——通过随机性赋上不同的爆炸倒计时。
在这里为了方便观察将N和M设为10,保存发射器粒子观察随机性。
与喷泉相比爆炸系统更加复杂,发射器会发射两种粒子,故我们需要添加第三种粒子:外壳粒子PT_SHELL。外壳粒子会随机时间爆炸,故我们需要获得一个随机数来定义爆炸时间。我们先定义一个方法来获得[-1, 1]间的随机数。
float RandNum(float offset) { // 使用游戏时间加上偏移值来从随机纹理采样 float u = (g_GameTime + offset); // 在[-1,1] float v = g_RandomVecMap.SampleLevel(g_SamLinear, u, 0).x; return v; }
再通过以下计算使其落在粒子的最大存活时间内:
float Randomtime = (RandNum(i * g_GameTime) + 1) * 0.5f * g_AliveTime;
外壳粒子的初始年龄(Age)就是粒子存活时间减去获得的随机爆炸时间:
p.Age = g_AliveTime - Randomtime;
这样就可以在外壳粒子生命周期结束时产生新的普通粒子。
完整的Explosion_SO_GS如下:
#include "Explosion.hlsli" [maxvertexcount(11)] void GS(point VertexParticle gIn[1], inout PointStream<VertexParticle> output) { gIn[0].Age += g_TimeStep; if (gIn[0].Type == PT_EMITTER) { // 是否到时间发射新的粒子 if (gIn[0].Age > g_EmitInterval) { uint ShellParticleCount = 10; [unroll] for (int i = 0; i < ShellParticleCount; i++) { float3 vRandom = RandUnitVec3(i * g_GameTime); float Randomtime = (RandNum(i * g_GameTime) + 1) * 0.5f * g_AliveTime; VertexParticle p; p.InitialPosW = g_EmitPosW.xyz; p.InitialVelW = 5.0f * vRandom; p.SizeW = float2(2.0f, 2.0f); p.Age = g_AliveTime - Randomtime; p.Type = PT_SHELL; output.Append(p); } // 重置时间准备下一次发射 gIn[0].Age = 0.0f; } // 总是保留发射器 output.Append(gIn[0]); } else if (gIn[0].Type == PT_SHELL) { if (gIn[0].Age > g_AliveTime) { uint FlareParticleCount = 10; [unroll] for (int i = 0; i < FlareParticleCount; i++) { float3 vRandom = RandUnitVec3(i * g_GameTime * 0.9f); VertexParticle p; p.InitialPosW = gIn[0].InitialPosW; p.InitialVelW = 10.0f * vRandom; p.SizeW = float2(1.0f, 1.0f); p.Age = 0; p.Type = PT_FLARE; output.Append(p); } } else { gIn[0].InitialPosW = gIn[0].InitialPosW + g_TimeStep * gIn[0].InitialVelW; gIn[0].InitialVelW = gIn[0].InitialVelW * (1 + g_AccelW * g_TimeStep); output.Append(gIn[0]); } } else { // 用于限制粒子数目产生的特定条件,对于不同的粒子系统限制也有所变化 if (gIn[0].Age <= g_AliveTime) { gIn[0].InitialPosW = gIn[0].InitialPosW + g_TimeStep * gIn[0].InitialVelW; gIn[0].InitialVelW = gIn[0].InitialVelW * (1 + g_AccelW * g_TimeStep); output.Append(gIn[0]); } } }
在位置和速度计算中,g_AccelW是粒子运动中受到的空气阻力产生的加速度,忽略重力影响。
演示
下面的动图演示喷泉和爆炸效果:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号