从0开始的字符串学习--KMP与失配树

-1、序

（我也不知道为什么一篇瞎写的学习笔记会有序qwq）

一开始学字符串的时候大多算法都是只记了下流程，并没有深入理解，于是准备重新整理一下字符串相关的一些东西，就有了这篇Blog。

0、符号及约定

（以下定义仅适用于本篇Blog）

$\varepsilon$：空串，即不含任何字符的字符串；

$S, T, \ldots$：字符串（若不做特殊说明，下文中大写字母均表示字符串）；

$|S|$：$S$的长度；

$S_i$：$S$的第$i$个字符（从$1$开始标号，即$i \in [1, |S|]$）；

$S_{l \ldots r}$：由$S_l, S_{l+1}, \ldots, S_r$组成的子串；

$prefix(S)$：$S$的前缀集，即$\{S_{1 \ldots i} | i \in [1, |S|]\} \cup \{\varepsilon\}$；

$suffix(S)$：$S$的后缀集，即$\{S_{i \ldots |S|} | i \in [1, |S|]\} \cup \{\varepsilon\}$；

$T \subseteq S$：$T$是$S$的子串；

$T \subsetneqq S$：$T$是$S$的真子串，即$T \subseteq S \land T \neq S$；

$ABC\ldots$：由若干个字符串依次首尾相接形成的新字符串；

1、Border，周期与失配树

1.1、Border

我们称$T$为$S$的Border，当且仅当：$T \subsetneqq S \land T \in prefix(S) \land T \in suffix(S)$。记$Border(S)$为$S$的所有Border组成的集合。

于是就有了几个显而易见的性质：

性质1.1.1：$\varepsilon$是任何非空字符串的Border。

性质1.1.2：$S_{1 \ldots t} \in Border(S) \longleftrightarrow S_{1 \ldots t} = S_{|S|-t+1 \ldots |S|}$。

性质1.1.3（Border的传递性）：若$P$是$Q$的Border且$Q$是$S$的Border，那么$P$是$S$的Border。

证明：因为前缀、后缀均具有传递性，由Border的定义，易证Border具有传递性。

性质1.1.4：$T \in Border(S) \longleftrightarrow T_{1 \ldots |T|-1} \in Border(S_{1 \ldots |S|-1}) \land T_{|T|} = S_{|S|}$。

1.2、周期

我们称整数$t$是$S$的周期，当且仅当：$t \in [1, |S|-1] \land \forall i \in [1, |S|-t], S_i = S_{i+t}$，记作$t \mid S$。

性质1.2.1：对于$S$的非空前缀$T$，$T$是$S$的Border当且仅当$|S|-|T|$是$S$的周期，这意味着非空Border与周期一一对应。

证明：$|S|-|T| \mid S \longleftrightarrow \forall i \in [1, |T|], S_i = S_{i+|S|-|T|} \longleftrightarrow S_{1 \ldots |T|} = S_{|S|-|T|+1 \ldots |S|} \longleftrightarrow T \in Border(S)$。

性质1.2.2：对于$S$的真子串$T$，$|T|$是$S$的周期当且仅当$S$是一个由无限个$T$组成的串的子串（即$|T| \mid S \longleftrightarrow S \subseteq TT\ldots$）。

证明留作习题。

1.3、MaxBorder

我们将非空字符串$S$最长的Border称作它的MaxBorder，记作$MaxBorder(S)$。

性质1.3.1：$S$所有异于其MaxBorder的Border都是其MaxBorder的Border。

（即$T \in Border(S) \land T \neq MaxBorder(S) \rightarrow T \in Border(MaxBorder(S))$）。

证明：令$S$的MaxBorder为$B$。对于$S$中一个异于$B$的Border$T$，根据Border的定义可知$T$和$B$都是$S$的前缀，又因为$T$比$B$短，所以$T$是$B$的前缀。同理可证$T$也是$B$的后缀。于是易知$T$是$B$的Border。

1.4、失配树（Border Tree）

对于$S$的每一个前缀，将其与其MaxBorder连一条边，就会形成一颗以$\varepsilon$为根的树，称作失配树（或者Border Tree）。

举个栗子，对于字符串 abacabaa ，它的Border Tree如下图所示：

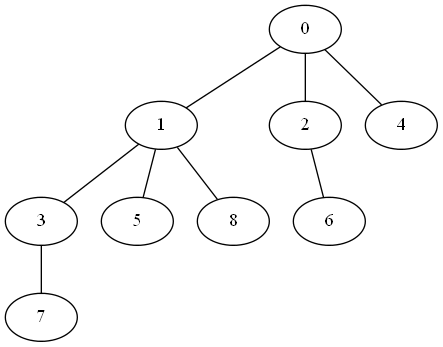
（节点标号为其代表的前缀长度）

性质1.4.1：对于$S$的两个前缀$P$和$Q$，$Q$是$P$的Border当且仅当$Q$在失配树上是$P$的祖先。

证明：由Border的传递性可证明其充分性，性质1.3.1可证明其必要性。

2、next数组与KMP算法

2.1、next

对于一个长度为$N$的字符串$S$，记$next_i = |MaxBorder(S_{1 \ldots i})|$。

根据性质1.1.4，我们可以由前$i-1$位的next找到满足$S_{1 \ldots j} \in Border(S_{1 \ldots i-1}) \land S_{j+1}=S_i$的$j$，从而递归求出$next_i=j$（当然，这样的$j$也有可能不存在，此时$next_i=0$）。

参考代码如下：

nxt[1]=0;
for(int i=2,j=0;i<=n;i++){
    while(j&&s[i]!=s[j+1])
        j=nxt[j];
    if(s[i]==s[j+1])
        j++;
    nxt[i]=j;
}

性质2.1.1：$next_i \leq next_{i-1}+1$。

2.2、字符串匹配问题以及BF算法

问题描述

给定一个长度为$N$的文本串$S$和一个长度为$M$模式串$T$，求出$T$在$S$中出现的全部位置。

BF(Brute Force)算法

BF算法的思想很暴力（毕竟名字就叫暴力算法），就是将$S$从每一位开始的长度为$m$的子串一一与$T$进行匹配，效率为$O(NM)$。

参考代码如下：

for(int i=1;i<=n;i++){
    bool flg=1;
    for(int j=1;j<=m;j++)
        if(s[i+j-1]!=t[j]){
            flg=0;
            break;
        }
    if(flg)
        printf("%d\n",i);
}

2.3、KMP(Knuth-Morria-Pratt)算法

从名字就知道，这是由D.E.Knuth、J,H,Morris 和 V.R.Pratt三人共同发明的一个字符串匹配算法。

注意到BF算法中某一位匹配失败后都要从模式串的开头重新匹配，导致效率很低。而KMP算法就是针对这点利用next数组进行优化：根据Border的性质，在某一位失配后，可以直接从模式串的next处接着匹配。这样减少了文本串指针的回跳，从而使复杂度降低到了线性。

参考代码（可以看出与上文求next的代码很像）：

for(int i=1,j=0;i<=n;i++){
    while(j&&s[i]!=t[j+1])
        j=nxt[j];
    if(s[i]==t[j+1])
        j++;
    if(j==m){
        printf("%d\n",j-m+1);
        j=nxt[j];
    }
}