牛客题集:练习赛67、68
练习赛67
D
dp[i][0]表示到了第i个位置,把前面的都变成0的最小操作数
dp[i][1]表示到了第i个位置,把前面的都变成1的最小操作数
最后输出min(dp[n][0],dp[n][1]+1))即可。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int #define pb push_back using namespace std; typedef long long ll; typedef unsigned long long ull; typedef double lf; typedef pair<ll, ll> pii; const int maxn = 1e6+10; const int N = 1500+10; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; const int hash_num = 131; const double eps=1e-6; const double PI=acos(-1.0); inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int n,a[maxn],f[maxn][2]; int main() { #ifndef ONLINE_JUDGE debug; #endif n=read(); for (int i = 1; i <= n; ++i) { a[i] =read(); } if (a[1]) f[1][1]=0,f[1][0]=1; else f[1][1]=1,f[1][0]=0; for (int i = 2; i <= n; ++i) { if (a[i]==1) { f[i][0]=min(f[i-1][1]+1,f[i-1][0]+1); f[i][1]=min(f[i-1][1],f[i-1][0]+1); } else { f[i][0]=min(f[i-1][0],f[i-1][1]+1); f[i][1]=min(f[i-1][0]+1,f[i-1][1]+1); } } cout << min(f[n][0],f[n][1]+1) <<endl; return 0; }
E
需要建立虚点来优化的最短路问题

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int #define pb push_back using namespace std; typedef long long ll; typedef unsigned long long ull; typedef double lf; typedef pair<ll, ll> pii; const int maxn = 1e6+35; const int N = 1500+10; const ll INF = 0x3f3f3f3f3f3f3f3f; const int mod = 1e9+7; const int hash_num = 131; const double eps=1e-6; const double PI=acos(-1.0); inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} struct node{ int to; ll dis; bool operator<(const node &b)const{ return dis>b.dis; } }; int n,t,a[maxn]; bool vis[maxn]; vector<int> v[maxn]; ll dis[maxn]; void dij(int s){ //s是起点,dis是结果 memset(vis,0,sizeof(vis)); memset(dis,INF,sizeof(dis)); dis[s]=0; //last[s]=-1; static priority_queue<node> q; q.push({s,0}); while(!q.empty()){ int u=q.top().to; q.pop(); if(vis[u])continue; vis[u]=1; for (ll j = 0; j < 32; ++j) if ((a[u]>>j)&1) { for(auto p:v[j]) { if(dis[p]>dis[u]+(1ll<<j)){ dis[p]=dis[u]+(1ll<<j); q.push({p,dis[p]}); //last[p]=x; //last可以记录最短路(倒着) } } v[j].clear(); } } } int main() { #ifndef ONLINE_JUDGE debug; #endif t=read(); while (t--) { n=read(); for (int i = 0; i < 32; ++i) v[i].clear(); for (int i = 1; i <= n; ++i) { a[i] =read(); } for (int i = 1; i <= n; ++i) { for (ll j = 0; j < 32; ++j) { if ((a[i]>>j)&1) v[j].pb(i); } } dij(1); if (dis[n] == INF) cout << "Impossible" <<endl; else cout << dis[n] <<endl; } return 0; }
F
对于区间【l,r】的答案,我们可以通过线段树来查询,如何建树?
假设【l,mid】的答案是 x1->y1的距离,【mid+1,r】的答案是 x2->y2的距离,那么【l,r】的答案肯定是 x1->y1、x1->y2、x2->y1、x2->y2这四个组合里面的最大那个。
怎么求树上点与点之间的距离?套用lca即可。
没调出来……
练习赛68
C
考虑离线每次查询的L,在最小生成树的过程中,我们每次是从小往大加边的,将L也按从小到大排序,每次加到一个比当前L要大的边的时候,之前的那些已经连上的边一定是都比L小的,所以在这些联通块中的点,两两之间的d(u,v)一定是比L小的,也就是符合条件,那么这时符合条件的点对的数量就是C(sz,2)(sz为每个联通块的大小)。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int #define pb push_back using namespace std; typedef long long ll; typedef unsigned long long ull; typedef double lf; typedef pair<ll, ll> pii; const int maxn = 1e6+10; const int N = 1500+10; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; const int hash_num = 131; const double eps=1e-6; const double PI=acos(-1.0); inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} struct Edge { ll u,v,w; bool operator<(const Edge&x) const { return w<x.w; } }G[maxn]; unsigned int SA, SB, SC; int n, m, q, LIM; ll L[maxn]; unsigned int rng61(){ SA ^= SA << 16; SA ^= SA >> 5; SA ^= SA << 1; unsigned int t = SA; SA = SB; SB = SC; SC ^= t ^ SA; return SC; } void gen(){ scanf("%d%d%d%u%u%u%d", &n, &m, &q, &SA, &SB, &SC, &LIM); for(int i = 1; i <= m; i++){ G[i].u = rng61() % n + 1; G[i].v = rng61() % n + 1; G[i].w = rng61() % LIM; } for(int i = 1; i <= q; i++){ L[i] = rng61() % LIM; } } struct DSU{ int a[maxn],sz[maxn]; void init(int n){ iota(a,a+n+1,0); fill(sz,sz+n+1,1); } int fa(int x){ return a[x]==x?x:a[x]=fa(a[x]); } bool query(int x,int y){ //查找 return fa(x)==fa(y); } void join(int x,int y){ //合并 x=fa(x),y=fa(y); if(x==y)return; if(sz[x]>sz[y])swap(x,y); a[x]=y; sz[y]+=sz[x]; } int operator[](int x){return fa(x);} }d; ll ans,res; int main() { #ifndef ONLINE_JUDGE debug; #endif gen(); d.init(n); sort(L+1,L+1+q); sort(G+1,G+1+m); int pos=1; for (int i = 1; i <= m; ++i) { int x=d[G[i].u]; int y=d[G[i].v]; if (x!=y) { while (pos<=q && G[i].w>L[pos]) ans^=res,pos++; res += 1ll*d.sz[x]*d.sz[y]; d.join(G[i].u,G[i].v); } } for (int i = pos; i <= q; ++i) ans^=res; cout << ans <<endl; return 0; }
D
对于每个位置 i ,每个回合都只会由 i-1、i、i+1转移过来,那么就是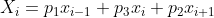
对于每个位置做这样的转换,写出矩阵形式就是这样
 (图侵删)
(图侵删)
k轮不就是做k次转换就是k次方吗?

但是普通快速幂的时间复杂度会超时,所以我们得知道什么是循环矩阵?
循环矩阵介绍:https://www.luogu.com.cn/blog/water-mi/2333333-233333
就可以把时间n^3降低乘n^2了。
依旧是没调出来……





