备战CCPC 练题集

真题练习

2019 CCPC 秦皇岛站

A、Angle Beats

做法就是枚举给中的点是直角顶点或是其他点是直角顶点

极角排序是想到了，但是有个地方有点想歪，结果发现想多了……，过后看到别人的优秀解题方法，先枚举了一条直角边，然后直接map重载，用map.count直接统计另一条直角边上的点数量。一开始不知道怎么用map来快速实现的，结果发现重载一下就行。设置两个虚拟点，比如枚举的那个除顶点外直角边的点是（x1,y1），那么虚拟点就是（-y1,x1）和（y1,-x1）。为什么是这两个点，因为根据直角判断 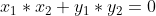 ，这两个点必定各自在直角所在直线的两侧，那么我们再寻找其他点，如果有一个点与任意一个虚拟点的叉积为0，那么就是说明在同一条边上，map直接判定它与虚拟点相等，数量++。

 

F、Forest Program

仙人掌树，找环的数量，然后乘法原理直接算出答案。

发现模板有一模一样的仙人掌树代码，提醒我该复习复习模板了

 

I、Invoker

常规dp

每种情况都有6种排序，写出来的代码比较繁琐导致拖的时间太长，但是真正比赛的时候，应该很难不受干扰

 

J、MUV LUV EXTRA

kmp的理解

 

2019 CCPC 哈尔滨站

E. Exchanging Gifts

题意理解错n遍

对于只统计第n种数组的最大开心值，如果这个是1操作，那还好说，如果是2操作，那我们要考虑要怎么把那些组成起来的数组统计起来。

首先，倒着寻找，比如，n数组是由 x1 和 y1组成，那么x1 和y1出现次数+1，如果x1 由x2 和y2 组成，那么就x2+=x1出现次数，y2+=x1出现次数，以此类推。

然后，再把所以数组扫一遍，如果他是1操作的数组且有出现次数，那么我们直接统计起来，就能全部找到第n种数组所有组成值。

#include <bits/stdc++.h>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
#define pb push_back
using namespace std;
typedef long long ll;
typedef double lf;
typedef pair<ll, ll> pii;
const int maxn = 1e6+10;
const ll INF = 0x3f3f3f3f3f;
const int mod = 1e9+7;
const double eps=1e-5;
const double PI=acos(-1.0);
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
vector<ll> MAP[maxn];
ll sum,used[maxn],maxx;
int t,n,i,op,m,j,x,y;
int main()
{
    t=read();
    while (t--)
    {
        n=read();
        
        for (i=1;i<=n;i++)
        {
            used[i]=0;
            op=read();
            if (op==1)
            {
                m=read();
                MAP[i].pb(op);
                for (j=1;j<=m;j++) 
                {
                    x=read();
                    MAP[i].pb(x);
                }
                
            }
            else
            {
                x=read(),y=read();
                MAP[i].pb(op);
                MAP[i].pb(x),MAP[i].pb(y);
            }
        }
        unordered_map<int,ll> mapp;
        used[n]=1;
        for (i=n;i;i--)
        {
            if (MAP[i][0]==2)
                used[MAP[i][1]]+=used[i],used[MAP[i][2]]+=used[i];
        }
        sum=maxx=0;
        for (i=1;i<=n;i++)
        {
            if (MAP[i][0]==1&&used[i]>0) 
                for (j=1;j<MAP[i].size();j++)
                {
                    mapp[MAP[i][j]]+=used[i];
                    sum+=used[i];
                    maxx=max(maxx,mapp[MAP[i][j]]);
                }
        }
        if (maxx*2>sum) printf("%lld\n",2*(sum-maxx));
            else printf("%lld\n",sum);    
        for (i=1;i<=n;i++) MAP[i].clear();
    }
    return 0;
}