day4——2020牛客暑期多校训练营
B
对于函数每递归一次,都要乘个c在里面,所以我们就可以知道只要因子足够多,乘以的c就足够多,值就越大,那么我们就从小到大每个因子都枚举一遍,计算每个因子能乘多少次。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 1e6+7; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int n,c,t,i; ll ans; int main() { t=read(); while (t--) { n=read(),c=read(); ans=1; for (i=2;i*i<=n;i++) { while (n%i==0) { n/=i; ans=ans*c%mod; } } if (n!=1) ans=ans*c%mod; printf("%lld\n",ans); } return 0; }
F
普通做法就是每种情况都判断一下
而这里看到的是别人的优秀做法
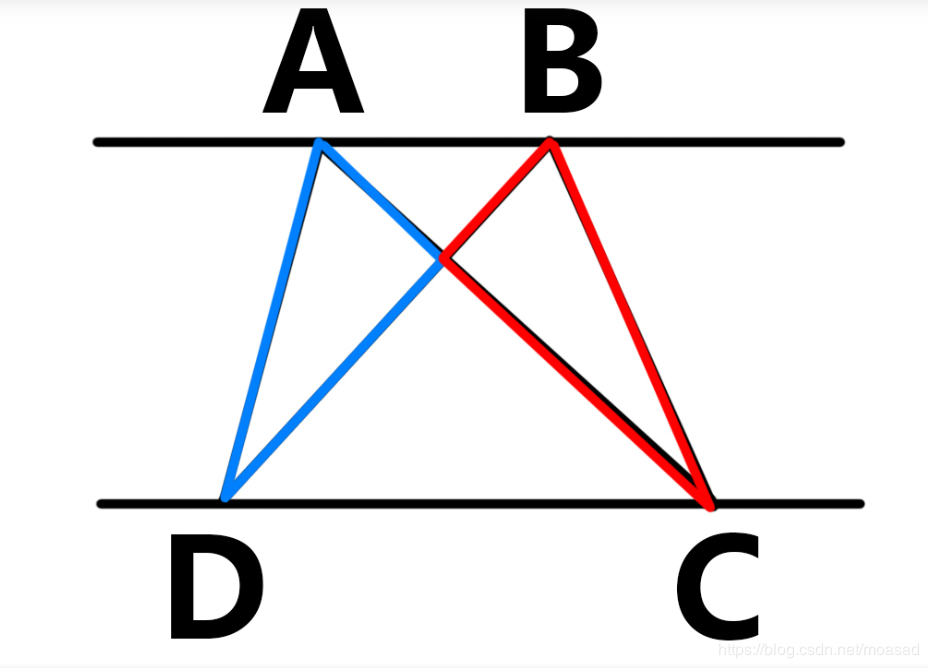
我们可以看成有两个三角形
由于三角形任意的俩边之和大于第三边,所以可以直接判断ad + bc和ac + bd的大小情况

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 1e6+7; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int t,a,b,c,d; int main() { t=read(); while (t--) { a=read(),b=read(),c=read(),d=read(); if (a+d<b+c) { printf("AB//CD\n"); } else printf("AB//DC\n"); } return 0; }
H
因为一个素数越大,与他匹配的数就会越少,所以考虑优先匹配较大的素数。两两匹配的情况下,对于数总量为单数的时候,我们肯定不能轻易浪费掉最后一个,这时我们可以把它分给2的倍数进行匹配。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 1e6+7; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int p[maxn],n,t,cnt,ans[maxn],tot,i,j,pos; bool vis[maxn],a[maxn]; void get_prime() { for (ri i=2;i<=2e5;i++) { if (!a[i]) p[cnt++]=i; for (ri j=0;j<cnt&&i*p[j]<=2e5;j++) { a[i*p[j]]=true; if (i%p[j]==0) break; } } } int main() { get_prime(); //for (i=0;i<=100;i++) cout<<p[i]<<endl; t=read(); while (t--) { n=read(); tot=0; for (i=1;i<=n;i++) vis[i]=0; pos=upper_bound(p,p+cnt,n/2)-p-1; for (i=pos;i>=0;i--) { for (j=p[i];j<=n;j+=p[i]) { if (vis[j] || j==(p[i]*2)) continue; ans[++tot]=j,vis[j]=1; } if (tot&1) vis[p[i]*2]=1,ans[++tot]=(p[i]*2); } printf("%d\n",tot/2); for (i=1;i<=tot;i+=2) printf("%d %d\n",ans[i],ans[i+1]); } return 0; }
I
看到题目很长+有段随机代码=劝退
但是后面翻别人题解的时候,才发现题目描述中十分隐晦的表明了那个 1/S 其实没什么用,直接[0,lcm(m,S)−1] 里面取个2,找连通超过m/2的点就可以了。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 333; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int n,m,i,f[maxn][maxn],ans[maxn],j,cnt,num,len,sum,t; string s; vector <int> tmp; int main() { t=read(); while (t--) { n=read(),m=read(); cin>>s; memset(f,0,sizeof(f)); for (i=0;i<=n-1;i++) f[i][i]=1; cnt=0; for (i=0;i<=n-1;i++) for (j=i+1;j<=n-1;j++) f[j][i]=f[i][j]=(s[cnt++]=='1'); memset(ans,-1,sizeof(ans)); num=0; for (i=0;i<=n-1;i++) if (ans[i]==-1) { ans[i]=num++; tmp.clear(); for (j=0;j<=n-1;j++) if (f[i][j]==1 && ans[j]==-1) tmp.push_back(j); tmp.push_back(i); len=tmp.size(); for (j=0;j<=n-1;j++) if (ans[j]==-1) { sum=0; for (auto u:tmp) { if (f[u][j]) sum++; } if (sum>=len/2) ans[j]=ans[i]; } } for (i=0;i<=n-1;i++) printf("%d ",ans[i]); cout<<endl; } return 0; }




