计算几何——凸包专题

凸包，即在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为 X的凸包。

通俗一点，凸包可以想象为一条刚好包住所有点的橡皮圈。

 

如何求得凸包？

这里将使用的是Andrew算法

Andrew算法的大体思路，我们分两次来求这个凸包，第一遍我们求出下凸包、第二遍我们求出上凸包，两者合起来就是一整个凸包。

首先我们按坐标 (x,y) 字典升序排序；

然后对于这n个有序点进行扫描，从左到右求出下凸包，具体方法为：
先将P1,P2放入凸包的边，然后从第三个点P3开始，判断P3是否能加入凸包里面，这里就要用到叉积进行运算来判断P3点是在边P1P2的左边还是右边。

同理从右到左求出上凸包。

以此来求得整个凸包。

vector<vec> st;
void push(vec &v,int b)
{
    while(st.size()>b
    && cross(*++st.rbegin(),st.back(),v)<=0) //会得到逆时针的凸包
        st.pop_back();
    st.push_back(v);
}
void convex(vec a[],int n)
{
    st.clear();
    sort(a,a+n,cmp_xy);
    for (ri i=0;i<n;i++) push(a[i],1);
    int b=st.size();
    for (ri i=n-2;i>=0;i--) push(a[i],b);
}

 

POJ - 3348

把题目的凸包求出来之后，我们就要算出它的面积出来，同样是用叉积来算面积。

求多边形面积（按顺序输入点的位置，顺时针逆时针、凹凸边形都可）：

    lf area=0;
    for (i=0;i<st.size();i++)
        if (i==st.size()-1) area+=cross(st[i],st[0]);
            else area+=cross(st[i],st[i+1]);
    area/=2;

面积求出来可能是负的结果，这与多边形顶点是在右手系还是左手系有关，我们取绝对值即可。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<cctype>
#include<iostream>
#include<algorithm>
//#include<chrono>
#include<vector>
#include<list>
#include<queue>
#include<string>
#include<set>
#include<map>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
using namespace std;
typedef long long ll;
typedef double lf;
typedef pair<int, int> pii;
const int maxn = 10050+10;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
const double eps=1e-8;
const double PI=acos(-1.0);
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int sgn(double x)
{
    if(fabs(x)<eps) return 0;
    if(x<0) return -1;
    else return 1;
}
struct vec{
    lf x,y;
    int num;
    vec(lf x=0,lf y=0):x(x),y(y){}
    vec operator-(const vec &b){return vec(x-b.x,y-b.y);}
    vec operator+(const vec &b){return vec(x+b.x,y+b.y);}
    vec operator*(lf k){return vec(k*x,k*y);}
    lf operator ^(const vec &b){return x*b.y-y-b.x;}
    lf len(){return hypot(x,y);}
    lf sqr(){return x*x+y*y;}
    /*截取*/vec trunc(lf k=1){return *this*(k/len());}
    /*逆时针旋转*/vec rotate(double th){lf c=cos(th),s=sin(th); return vec(x*c-y*s,x*s+y*c);}
}p[maxn];
lf cross(vec a,vec b){return a.x*b.y-a.y*b.x;};
lf cross(vec a,vec b,vec c){return cross(a-b,b-c);}
lf dot(vec a,vec b){return a.x*b.x+a.y*b.y;}
bool cmp_xy(const vec &a,const vec &b){return make_pair(a.x,a.y)<make_pair(b.x,b.y);}
bool cmp_atan(const vec &a,const vec &b){return atan2(a.x,a.y)<atan2(b.x,b.y);}
/*输出*/ostream &operator<<(ostream &o,const vec &v){return o<<'('<<v.x<<','<<v.y<<')';}
vector<vec> st;
void push(vec &v,int b)
{
    while(st.size()>b
    && cross(*++st.rbegin(),st.back(),v)<=0) //会得到逆时针的凸包
        st.pop_back();
    st.push_back(v);
}
void convex(vec a[],int n)
{
    st.clear();
    sort(a,a+n,cmp_xy);
    for (ri i=0;i<n;i++) push(a[i],1);
    int b=st.size();
    for (ri i=n-2;i>=0;i--) push(a[i],b);
}
int main()
{
    lf area=0;
    int n,i,ans;
    n=read();
    for (i=0;i<n;i++) cin>>p[i].x>>p[i].y;
    convex(p,n);
    for (i=0;i<st.size();i++)
        if (i==st.size()-1) area+=cross(st[i],st[0]);
            else area+=cross(st[i],st[i+1]);
    area/=2;
    if (area<=0) area=-area;
    ans=area/50;
    cout<<ans<<endl;
    return 0;
}

 

POJ - 1113

题目意思大概如下图，要求出走一周的路程，即凸包周长+一个完整的圆周长。

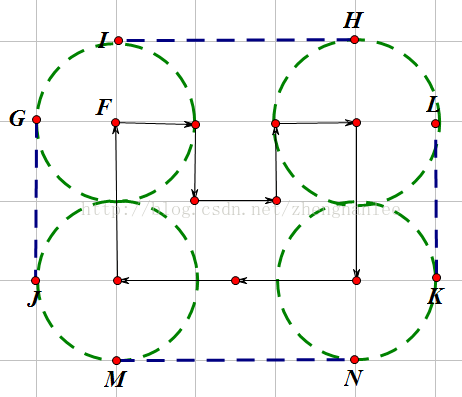侵删

#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<cctype>
#include<iostream>
#include<algorithm>
//#include<chrono>
#include<vector>
#include<list>
#include<queue>
#include<string>
#include<set>
#include<map>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
using namespace std;
typedef long long ll;
typedef double lf;
typedef pair<int, int> pii;
const int maxn = 10050+10;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
const double eps=1e-8;
const double PI=acos(-1.0);
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int sgn(double x)
{
    if(fabs(x)<eps) return 0;
    if(x<0) return -1;
    else return 1;
}
struct vec{
    lf x,y;
    int num;
    vec(lf x=0,lf y=0):x(x),y(y){}
    vec operator-(const vec &b){return vec(x-b.x,y-b.y);}
    vec operator+(const vec &b){return vec(x+b.x,y+b.y);}
    vec operator*(lf k){return vec(k*x,k*y);}
    lf operator ^(const vec &b){return x*b.y-y-b.x;}
    lf len(){return hypot(x,y);}
    lf sqr(){return x*x+y*y;}
    /*截取*/vec trunc(lf k=1){return *this*(k/len());}
    /*逆时针旋转*/vec rotate(double th){lf c=cos(th),s=sin(th); return vec(x*c-y*s,x*s+y*c);}
}p[maxn],p0;
lf cross(vec a,vec b){return a.x*b.y-a.y*b.x;};
lf cross(vec a,vec b,vec c){return cross(a-b,b-c);}
lf dot(vec a,vec b){return a.x*b.x+a.y*b.y;}
bool cmp_xy(const vec &a,const vec &b){return make_pair(a.x,a.y)<make_pair(b.x,b.y);}
bool cmp_atan(const vec &a,const vec &b){return atan2(a.x,a.y)<atan2(b.x,b.y);}
/*输出*/ostream &operator<<(ostream &o,const vec &v){return o<<'('<<v.x<<','<<v.y<<')';}
vector<vec> st;
int n,L,i;
lf ans;
void push(vec &v,int b)
{
    while(st.size()>b
    && cross(*++st.rbegin(),st.back(),v)<=0) //会得到逆时针的凸包
        st.pop_back();
    st.push_back(v);
}
void convex(vec a[],int n)
{
    st.clear();
    sort(a,a+n,cmp_xy);
    for (ri i=0;i<n;i++) push(a[i],1);
    int b=st.size();
    for (ri i=n-2;i>=0;i--) push(a[i],b);
}
int main()
{
    while (~scanf("%d%d",&n,&L))
    {
        ans=0;
        for (i=0;i<n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
        convex(p,n);
        for (i=0;i<st.size();i++)
        {
            if (i==st.size()-1) ans+=(st[i]-st[0]).len();
                else ans+=(st[i]-st[i+1]).len();
        }
        ans+=PI*L*2.0;
        cout<<int(ans+0.5)<<endl;
    }
    return 0;
}

 

POJ - 1228

有关凸包稳定性的探究。

对于凸包的一条边，如果边上只有两个端点，那么在边外加入一个点，即可破坏这条边，重新构成一个更大的凸包，原有边的两个端点仍在新凸包上，则说明旧凸包不是稳定的。

而边上有大于等于三个端点时，那么在边外加入一个点，我们破坏了这条边，重新构成一个更大的凸包时，原有边上除两个端点外的点将不在新凸包上，则说明旧凸包是稳定的。

因此判断凸包是否稳定，只需判断一条边上是否有三个及以上的点。即判断某个点是否在一条边上（除端点）。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<cctype>
#include<iostream>
#include<algorithm>
//#include<chrono>
#include<vector>
#include<list>
#include<queue>
#include<string>
#include<set>
#include<map>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
using namespace std;
typedef long long ll;
typedef double lf;
typedef pair<int, int> pii;
const int maxn = 10050+10;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
const double eps=1e-8;
const double PI=acos(-1.0);
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int sgn(double x)
{
    if(fabs(x)<eps) return 0;
    if(x<0) return -1;
    else return 1;
}
struct vec{
    lf x,y;
    int num;
    vec(lf x=0,lf y=0):x(x),y(y){}
    vec operator-(const vec &b){return vec(x-b.x,y-b.y);}
    vec operator+(const vec &b){return vec(x+b.x,y+b.y);}
    vec operator*(lf k){return vec(k*x,k*y);}
    lf operator ^(const vec &b){return x*b.y-y-b.x;}
    lf len(){return hypot(x,y);}
    lf sqr(){return x*x+y*y;}
    /*截取*/vec trunc(lf k=1){return *this*(k/len());}
    /*逆时针旋转*/vec rotate(double th){lf c=cos(th),s=sin(th); return vec(x*c-y*s,x*s+y*c);}
}p[maxn],p0;
lf cross(vec a,vec b){return a.x*b.y-a.y*b.x;};
lf cross(vec a,vec b,vec c){return cross(a-b,b-c);}
lf dot(vec a,vec b){return a.x*b.x+a.y*b.y;}
bool cmp_xy(const vec &a,const vec &b){return make_pair(a.x,a.y)<make_pair(b.x,b.y);}
bool cmp_atan(const vec &a,const vec &b){return atan2(a.x,a.y)<atan2(b.x,b.y);}
/*输出*/ostream &operator<<(ostream &o,const vec &v){return o<<'('<<v.x<<','<<v.y<<')';}
vector<vec> st;
int n,i,t,j,cnt;
lf ans;
void push(vec &v,int b)
{
    while(st.size()>b
    && cross(*++st.rbegin(),st.back(),v)<=0) //会得到逆时针的凸包
        st.pop_back();
    st.push_back(v);
}
void convex(vec a[],int n)
{
    st.clear();
    sort(a,a+n,cmp_xy);
    for (ri i=0;i<n;i++) push(a[i],1);
    int b=st.size();
    for (ri i=n-2;i>=0;i--) push(a[i],b);
}
bool check(vec p,vec a,vec b)
{
    return sgn(cross(a-p,b-p))==0 && sgn(dot(a-p,b-p))<=0;
}
int main()
{
    t=read();
    while (t--)
    {
        scanf("%d",&n);
        for (i=0;i<n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
        if (n<=5) 
        {
            cout<<"NO"<<endl;
            continue;
        }
        convex(p,n);
        if (st.size()<=2) 
        {
            cout<<"NO"<<endl;
            continue;
        }
        for (i=0;i<st.size();i++)
        {
            cnt=0;
            for (j=0;j<n;j++)
                if (check(p[j],st[i],st[(i+1)%st.size()])) cnt++;
            if (cnt<3) break;
        }
        if (i==st.size()-1) cout<<"YES"<<endl;
            else cout<<"NO"<<endl;
    }
    return 0;
}