解法——逆向思维
很多时候,解题需要逆向思维。
最为普遍的就是出现在容斥的题目里面,其他题型的题目逆向思维也会有可能用到,当我们遇到这种题目的时候往往正向解题时无思路或者十分复杂,但是运用逆向思维会变得轻松很多。
1.容斥
同色三角形问题 https://ac.nowcoder.com/acm/contest/4137/F
经典题目,同色三角形个数=所有三角形个数-不同色三角形个数
我们可以看到这题不同色的情况只会有两种:一种是两黑一白,另一种是两白一黑
对于其中一种情况,我们这么处理:
对于三角形的三个点,每个点与之连接两条边,如果两条边颜色不同则sum+1,那么一个不同色的三角形,统计出来sum=2。
那么只需最后sum/2,即得出一个不同色三角形个数。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 5010; const int INF = 0x3f3f3f3f; const int mod = 998244353; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int du[maxn][2],i,j; ll n,A,B,C,P,D,ans,now; int main() { n=read(); ans=0; A=read(),B=read(),C=read(),P=read(),D=read(); for(i=1;i<=n;i++) { for(j=i+1;j<=n;j++) { now=(A*(i+j)%P*(i+j)%P+B*(i-j)%P*(i-j)%P+C)%P; if(now<=D) { du[i][0]++; du[j][0]++; } else { du[i][1]++; du[j][1]++; } } } for(i=1;i<=n;i++) ans+=du[i][0]*du[i][1]; cout<<n*(n-1)*(n-2)/6-ans/2<<endl; return 0; }
2.搜索
2015-2016 ACM-ICPC, NEERC, Moscow Subregional Contest K. King’s Rout
题意:希望你构造出一种符合以下条件的拓扑序。
1、拓扑序
2、在满足上述条件的情况下,让1尽可能地靠前。
3、在满足上述条件的情况下,让2尽可能地靠前。
…
n、在满足上述条件的情况下,让n尽可能地靠前。
如果正着拓扑,那么我们是很难得出答案的,我们来看一个例子
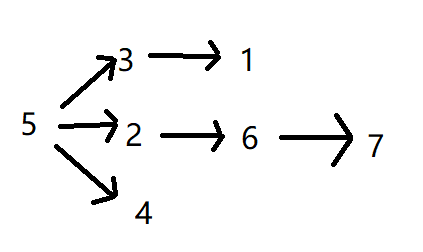
如果只是贪心的取当前最小值来拓扑,则得出序列是【5,2,3,1,4,6,7】,而答案得出的序列是【5,3,1,2,4,6,7】,所以正着拓扑的话,很难处理
那逆着建图,逆着拓扑呢?我们逆着拓扑取当前最大值来拓扑会不会得出答案序列?答案是会的。
因为我早点找出当前最大值,就等价于把小的值留在最后面,把这种方法得出来的序列倒过来看,就是答案要求的序列。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 2e5+10; const int INF = 0x3f3f3f3f; const int mod = 998244353; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} priority_queue<int> q; map<pii,int> mapp; vector <int> G[maxn]; int n,du[maxn],m,a,b,ans[maxn],cnt,i; void toposort() { for (ri i=1;i<=n;i++) { if (du[i]==0) q.push(i); } while (!q.empty()) { int u=q.top(); q.pop(); ans[cnt++]=u; for (auto v:G[u]) if (--du[v]==0) q.push(v); } } int main() { n=read(),m=read(); for (i=1;i<=m;i++) { a=read(),b=read(); G[b].push_back(a); du[a]++; } toposort(); for (i=cnt-1;i>=0;i--) cout<<ans[i]<<" "; return 0; }
2014-2015 ACM-ICPC, Asia Xian Regional Contest H. The Problem to Make You Happy
题意:在一张有向图,在图中的两个节点上面有两个棋。Alice和Bob在上面移动棋子,如果Bob不能移动或是两个棋子在同一个节点上,那就算Bob输。
用原来计算SG函数的方法进行记忆化搜索?这样做很烦很乱。
那正着来想一筹莫展,逆着来呢?
Bob输有两种方式,一种不能移动另一种两个棋子在同一个节点上,我们把这两种方式做为必败态的起点,进而一个个推导出能到达必败态的每一个状态。
设状态f[bob‘s当前所在点][alice‘s当前所在点][谁正在下棋]
那么 f[bob‘s当前所在点][alice‘s当前所在点][bob 正在下] 能推导出 f[bob‘s当前所在点][alice‘s上一个所在点][alice 正在下],同理另一种状态

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 105; const int INF = 0x3f3f3f3f; const int mod = 998244353; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} struct node { int x,y,step; }; int t,n,m,u,v,du[maxn],i,j,a,b,cnt[maxn][maxn],x,cas,y,f[maxn][maxn][2]; bool G[maxn][maxn]; int main() { t=read(); while (t--) { n=read(),m=read(); memset(G,false,sizeof(G)); memset(du,0,sizeof(du)); memset(f,0,sizeof(f)); memset(cnt,0,sizeof(cnt)); while (m--) { x=read(),y=read(); G[y][x]=true; du[x]++; } a=read(),b=read(); queue<node> q; for (i=1;i<=n;i++) { f[i][i][0]=1; q.push({i,i,0}); f[i][i][1]=1; q.push({i,i,1}); } for (i=1;i<=n;i++) for (j=1;j<=n;j++) if (i-j && du[i]==0) { f[i][j][0]=1; q.push({i,j,0}); } while (!q.empty()) { node u=q.front(); q.pop(); x=u.x,y=u.y; if (u.step==1) { for (j=1;j<=n;j++) if (G[x][j]) { if (++cnt[j][y]==du[j])//如果从j出发的所有的状态都是必败态,那么f[j][y][0]本身也是必败态 { if (f[j][y][0]) continue; f[j][y][0]=1; q.push({j,y,0}); } } } else { for (j=1;j<=n;j++)//Alice可以选择一条路使得Bob必败 if (G[y][j]) { if (f[x][j][1]) continue; f[x][j][1]=1; q.push({x,j,1}); } } } printf("Case #%d: ",++cas); if (f[a][b][0]) cout<<"No"<<endl; else cout<<"Yes"<<endl; } return 0; }
3.记录变量方面
HDU - 5245
题意:给你一个M×N的矩阵,你可以选K次,每次选择两个点(x1,y1)和(x2,y2),将这两个点围成的子矩阵涂上颜色,求预计涂色的格子的个数。
因为每个格子若能被涂色,都会结果造成贡献,所以一个一个格子来考虑。
我们可以考虑先计算一个格子不被涂色的概率,然后再1-不涂色概率就得出此格子被涂色的概率
如图,我们计算红色格子不被涂色的概率,那么就要算出选择的两个点(x1,y1)和(x2,y2)都是黄色格子的概率,把其切成几个矩形来计算即可。


#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 2e5+10; const int INF = 0x3f3f3f3f; const int mod = 998244353; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} double qpow(double p,ll q){return (q&1?p:1)*(q?qpow(p*p,q/2):1);} ll m,n,k,i,j,q,t; double sum,num; int main() { t=read(); for (q=1;q<=t;q++) { m=read(),n=read(),k=read(); sum=num=0; for (i=1;i<=m;i++) for (j=1;j<=n;j++) { num+=(i-1)*n*(i-1)*n; num+=(j-1)*m*(j-1)*m; num+=(m-i)*n*(m-i)*n; num+=(n-j)*m*(n-j)*m; num-=(i-1)*(j-1)*(i-1)*(j-1); num-=(i-1)*(n-j)*(i-1)*(n-j); num-=(m-i)*(j-1)*(m-i)*(j-1); num-=(m-i)*(n-j)*(m-i)*(n-j); num/=n*m*n*m; sum+=1.0-qpow(num,k); } printf("Case #%d: %.0lf\n",q,sum); } return 0; }
2015-2016 ACM-ICPC, NEERC, Moscow Subregional Contest H. Hashing
题意:给出N个16进制的数,从中选出一个序列,问Σ j^(a[i]) 最大是多少,a[I]是选出来的数,j是这个数在序列中是第J个(从0开始计数)
我们发现,如果我们记录选中了多少个是O(n^2)的空间复杂度,是肯定不可行的,时间复杂度也不够。 我们可以猜想:不被选中的数的个数特别少。少到多少呢?这个不太好猜,但是肯定不会大于256。 所以我们就可以记录不被选中的数。 因此就可以用dp直接做了。

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 1e5+5; const int INF = 0x3f3f3f3f; const int mod = 998244353; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} int n,a[maxn],i,j; ll ans,f[maxn][260]; int main() { n=read(); for (i=1;i<=n;i++) scanf("%x",&a[i]); for (i=1;i<=n;i++) for (j=0;j<=min(i,256);j++) { if (j>0) f[i][j]=f[i-1][j-1]; f[i][j]=max(f[i][j],f[i-1][j]+(a[i]^(i-j-1))); ans=max(ans,f[i][j]); } cout<<ans<<endl; return 0; }





