round 631

A水题

 

B

只要正着数具备1~i区间的数，倒着数具备1~n-i+1区间的数，同时分别记录一下有没有数字重复情况，若都满足这些条件就说明有答案。

#include <bits/stdc++.h>
#define mp make_pair
using namespace std;
typedef long long ll;
const int maxn = 5e5+5;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int t,n,maxx,minn,cnt,num[maxn],i,a[maxn],ans[maxn];
bool tt,check[maxn];
int main()
{
    t=read();
    while (t--)
    {
        n=read();
        maxx=-INF,minn=INF;tt=true;
        for (i=1;i<=n;i++) num[i]=0;
        for (i=1;i<=n;i++)
        {
            a[i]=read();
            maxx=max(maxx,a[i]);
            minn=min(minn,a[i]);
            num[a[i]]++;
            if (num[a[i]]>1) tt=false;
            if (minn==1 && maxx==i && tt) check[i]=true;
                else check[i]=false;
        }
        maxx=-INF,minn=INF;tt=true;
        cnt=0;
        for (i=1;i<=n;i++) num[i]=0;
        for (i=n;i>=2;i--)
        {
            maxx=max(maxx,a[i]);
            minn=min(minn,a[i]);
            num[a[i]]++;
            if (num[a[i]]>1) tt=false;
            if (minn==1 && maxx==n-i+1 && tt && check[i-1])
                ans[++cnt]=i-1;
        }
        cout<<cnt<<endl;
        for (i=1;i<=cnt;i++)
            cout<<ans[i]<<" "<<n-ans[i]<<endl;
    }
    return 0;
}

 

C

我们知道最后一次涂颜色肯定是不会被覆盖的，最后一次颜色涂的有多长就显示多长。

所以考虑把最后一次涂在最后面，即1~n的长度，其中n-x+1~n这一段都是最后一次涂的。（x是最后一次涂颜色的长度）

然后我们就可以把倒数第二次、倒数第三次，倒着开始被涂在上一次的颜色上，只显示出一个格子的长度。

我们来举个例子

 

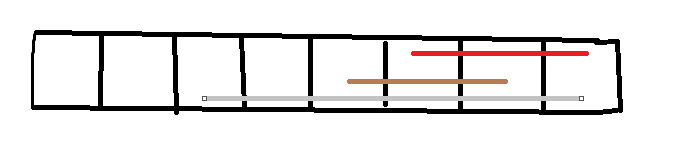
最后一次涂的是红色，第二次涂的是棕色，第一次涂的是灰色，如果倒数第二次颜色的长度<=（上一次涂的颜色的长度+1），则我们只需让这种颜色露出一个格子；如果像倒数第三次这种情况，涂的颜色太长，以至于必须要露出大于一个格子，就特殊处理。

但是题目要求所有格子要涂满，所以像上面图一样前两个格子是空的就不行，我们可以把第一次涂的颜色往回退，如果还有空的格子，再把第二次涂的颜色往回退，直到没有空格为止。

值得注意的是：如果怎么也涂不满，或是怎么涂都超过格子长度就说明无解。

#include <bits/stdc++.h>
#define mp make_pair
using namespace std;
typedef long long ll;
const int maxn = 2e5+10;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
inline int read(){int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int n,m,k,i,a[maxn],b[maxn],q;
ll sum;
int main()
{
    n=read(),m=read();
    k=n;
    for (i=1;i<=m;i++) 
    {
        a[i]=read();
        sum+=a[i];
    }
    if (sum<n || a[m]+m-1>n) cout<<-1<<endl;
    else
    {
        k-=a[m];
        b[m]=k+1;
        for (i=m-1;i;i--)
        {
            if (n-k+1>=a[i]) k--,b[i]=k+1;
                else k=n-a[i],b[i]=k+1;
        }
        if (k>=0)
        {
            q=1;
            for (i=1;i<=m;i++)
            {
                b[i]=q;
                if (k-a[i]+1<=0) break;
                else q+=a[i],k-=(a[i]-1);
            }
            for (i=1;i<=m;i++) cout<<b[i]<<" ";
        }
        else cout<<-1<<endl;
    }
    return 0;
}

 

D

题意要求：a数组要递增，b数组也要递增

因为b [ i ] = a[ i ] ^ a[ i-1 ] ^ ……a[ 1 ]，b [ i-1 ] = a[ i-1 ] ^ ……a[ 1 ]，因为b [ i ]>b [ i-1 ]，所以最后一个a[ i ]异或起来就显得尤为关键，我们假设b [ i-1 ]的最高位在x，因为a数组要递增，那么a[ i ]的最高位就只能在x+1，当然也可以x+2，x+3等等，如果选择x+1，那么2^x~2^x+1次方这里面的数随便选一个，如果选择x+2等等，那么2^x~2^x+1次方里面的数就不选，所以在2^x~2^x+1次方里面，选择的方式有2^x+1次。

运用一下乘法原理，乘起来得到方案数即可。同时要保证不超过d的限制以及要减去空集的这种情况。

#include <bits/stdc++.h>
#define mp make_pair
using namespace std;
typedef long long ll;
const int maxn = 2e5+10;
const int INF = 0x3f3f3f3f; 
//const int mod = 998244353;
inline int read(){int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
//ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int mod,d,t,p,i;
ll ans;
int main()
{
    t=read();
    while (t--)
    {
        d=read(),mod=read();
        ans=1;
        p=int(log2(d));
        for (i=0;i<p;i++)
            ans=ans*((1<<i)+1)%mod;
        ans=ans*(d-(1<<p)+1+1)%mod;
        cout<<((ans-1)%mod+mod)%mod<<endl;
    }
    return 0;
}

 

E

给个完全大根堆，然后要删掉2^g个点，如果对于某个节点 i 来说，节点 i 的子树的绝对高度大于了最后需要保留的高度，那么说明节点 i 的子树中必须删除掉一些节点才能保证降低子树的高度，而对于这棵子树来说，a[ i ] 一定是子树中的最大值，所以删掉节点 i 一定是最优的，为什么最优？因为是个大根堆。

#include <bits/stdc++.h>
#define mp make_pair
using namespace std;
typedef long long ll;
const int maxn = (1<<21)+100;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
inline int read(){int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
vector <int> ans;
int i,h,g,size,t,a[maxn];
ll sum;
int check(int x)
{
    if (!a[x*2] && !a[x*2+1]) return x;
    if (a[x*2]>a[x*2+1]) return check(x*2);
        else return check(x*2+1);
}
void dfs(int x)
{
    if (!a[x*2] && !a[x*2+1]) a[x]=0;
        else if (a[x*2]>a[x*2+1])
        {
            a[x]=a[x*2];
            dfs(x*2);
        }
        else
        {
            a[x]=a[x*2+1];
            dfs(x*2+1);
        }
}
int main()
{
    t=read();
    while (t--)
    {
        h=read(),g=read();
        for (i=1;i<(1<<(h+1));i++) a[i]=0;
        for (i=1;i<(1<<h);i++) a[i]=read();
        size=(1<<g)-1;ans.clear();
        for (i=1;i<(1<<g);i++)
            while (check(i)>size)
            {
                ans.push_back(i);
                dfs(i);
            }
        sum=0;
        for (i=1;i<(1<<g);i++) sum+=a[i];
        cout<<sum<<endl;
        for (i=0;i<ans.size();i++) cout<<ans[i]<<" ";
        cout<<endl;
    }
}