让我们对这棵树进行肢解吧——树链剖分

树链剖分，顾名思义，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、BST、SPLAY、线段树等）来维护每一条链。

这里我用的是线段树来维护，感觉应该算是最简单的，但这还是花了我一段时间去理解。//我觉得树链剖分讲解好的博客（https://www.cnblogs.com/ivanovcraft/p/9019090.html）

 

模板题：https://www.luogu.com.cn/problem/P3384

树链剖分，我觉得较为难的点有两个，一个是如何通过遍历这棵树得到树的重链和轻链，另一个是如何用线段树来维护链。

通过这道例题，我们来探寻其奥秘。

如何通过遍历这棵树得到树的重链和轻链？

首先来第一遍dfs，遍历这颗树，得到一些基本的东西，比如这个节点的父节点是谁 f [ ]，以x为根节点的子树内所有节点的总数 size[ ]，这个节点的在树里面的深度 d [ ]，以及   记录当前结点的子节点   里面拥有最多子节点数   的那个子节点 son[ ]。

如图所示

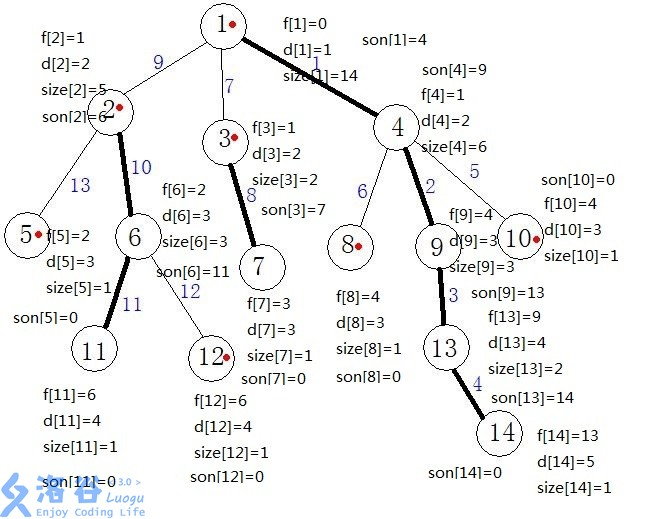
 我们可见，树上的边有些是加粗的边，有些是没有加粗的边。加粗的边连起来每一个节点，我们叫做重链；反之，我们叫做轻链。

你能看出来是怎么找出来重链轻链的吗？如果当前点有很多个子节点，我们仅需看子节点下面有多少个节点，找出最多的那个，然后与这个子节点相连的边就叫重边，一直找下去，可得到树里面所以的重边，然后形成重链。

比如我们看图上的 1号节点，他子节点有3个，我们发现 4号节点下面的节点数最多，于是 1 和 4 之间的边就叫重边；

4 号节点，他子节点有3个，我们发现 9号节点下面的节点数最多，于是 4 和 9 之间的边就叫重边。

如果出现像 6 号节点这种情况，他有两个子节点，但是子节点下面的节点数都为0，也就是下面的节点数相等，那么我们可随便找一条边作为重边。

 

然后做第二遍dfs，这次我们要把重链上的节点都标记一个共同祖先（深度最低的）top [ ]，然后通过优先走重链，再走轻链的方法，给每个节点标记上类似于时间戳的值 id [ ]，rk数组表示当前时间戳代表的哪个节点。

 

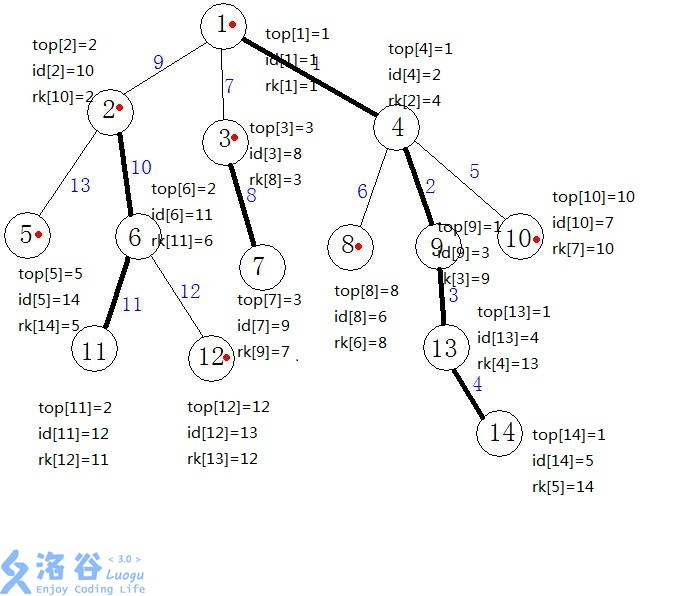
 top搞出来有什么用呢？怎么那么像并查集那样的？ 其实，top搞出来和后面的线段树操作有关，也是难点。

id又有什么用？我们可以联想一下，为什么并查集每次做完之后，都要把节点的father都改为一个共同祖先？原因就是为了加速，我们在查询两个点之间的关系时，如果不在一条重链上，我们可以直接把当前点跳到祖先那里，然后再看两者的关系，这是后面要说到的，id还有另一个妙用。

 

如何用线段树来维护链？

比如例题里面要求我们将树从x到y结点最短路径上所有节点的值都加上z。

分两种情况，

一 在同一条重链上面，

　　那就好办，我们再次看上图，你会发现重链上的id值都是连续的，这说明了我们可以用线段树来维护区间值，这个好理解。

二 不在同一条重链上面，那么我们要怎么做呢？

　　我们来看id值，刚刚讲到，我们在移动点的时候，可直接把当前点跳到他的共同祖先那里，跳的这个过程不能忽略，要用线段树维护，这时候维护的是一个区间（关系到>=2个点）。

　　但是这只适用于当前点在一条重链上面，如果不在重链上怎么办？那么我们只能一步一步的走，走的这个过程不能忽略，要用线段树维护，这时候维护的是一个点（只关系到1个点）。

最终有两种情况了

     1 我们把点都移到了同一条重链上面，如何判断？看id值两者是否相等。相等说明就在同一条重链上面，那么之后处理如第一种情况

　　2 我们把点移到了一条轻链上面。我们只能通过一步一步走，走到一起。

 

可能我们现在还是有点懵逼，我用一个表格来表示（依据上面那个图）

 

 可看到重链基本上涉及两个以上的区间，轻链在修改时只能类似去到一个点上面去修改。

比如我要改8 到 14 节点的值，最终改的是线段树区间里面的（2，5）和（6，6）。在程序里面操作不会直接（2，6）这么修改。

其实就一句话，涉及到轻链上面的改动或查询，一定是一个一个值的改，比如（6，6）、（7，7）；而不是直接（6，7）；而重链的话，可一个一个值改，也可一段一段改。

 

最后附上模板题代码：

 

#include <bits/stdc++.h>
#define maxn 1000005
using namespace std;
struct node
{
    int lazy,l,r,sum;
};
node a[maxn];
int op,x,y,z,mod,n,m,r,p,i,first[maxn],dis[maxn],next[maxn],value[maxn],zhi[maxn],tot,size[maxn],id[maxn],f[maxn],depth[maxn],son[maxn],top[maxn],cnt,rank[maxn];
void add(int x,int y)
{
    tot++;
    next[tot]=first[x];
    first[x]=tot;
    //value[tot]=v;
    zhi[tot]=y;
}
void dfs1(int x)
{
    int k;
    k=first[x],
    size[x]=1,
    depth[x]=depth[f[x]]+1;
    while (k!=-1)
    {
        if (zhi[k]!=f[x])
        {
            f[zhi[k]]=x,
            dfs1(zhi[k]),
            size[x]+=size[zhi[k]];
            if (size[son[x]]<size[zhi[k]]) son[x]=zhi[k];
        }
        k=next[k];
    }
}
void dfs2(int x,int t)
{
    top[x]=t;
    id[x]=++cnt;
    rank[cnt]=x;
    if (son[x]) dfs2(son[x],t);
    int k=first[x];
    while (k!=-1)
    {
        if (zhi[k]!=son[x] && zhi[k]!=f[x])
            dfs2(zhi[k],zhi[k]);
        k=next[k];
    }
}
void pushup(int num)
{
    a[num].sum=(a[num*2+1].sum+a[num*2].sum)%mod;
}
void pushdown(int num)
{
    if (a[num].lazy)
    {
        a[num*2].lazy=(a[num*2].lazy+a[num].lazy)%mod;
        a[num*2+1].lazy=(a[num*2+1].lazy+a[num].lazy)%mod;
        a[num*2].sum=(a[num*2].sum+(a[num*2].r-a[num*2].l+1)*a[num].lazy)%mod;
        a[num*2+1].sum=(a[num*2+1].sum+(a[num*2+1].r-a[num*2+1].l+1)*a[num].lazy)%mod;
        a[num].lazy=0;
    }
}
void build(int l,int r,int num)
{
    if (l==r)
    {
        a[num].sum=dis[rank[l]];
        a[num].l=a[num].r=l;
        return;
    }
    int mid=(l+r)>>1;
    build (l,mid,num*2),
    build (mid+1,r,num*2+1); 
    a[num].l=a[num*2].l;
    a[num].r=a[num*2+1].r;
    pushup(num);
}
void upgrade_3(int l,int r,int num,int value)
{
    if (l<=a[num].l && a[num].r<=r)
    {
        a[num].lazy=(a[num].lazy+value) % mod;
        a[num].sum=(a[num].sum+(a[num].r-a[num].l+1)*value)% mod;
        return;
    }
    pushdown(num);
    int mid=(a[num].l+a[num].r)/2;
    if (mid>=l) upgrade_3(l,r,num*2,value);
    if (mid<r) upgrade_3(l,r,num*2+1,value);
    pushup(num);
}
void upgrade_1(int x,int y,int value)
{
    while (top[x]!=top[y])
    {
        if (depth[top[x]]<depth[top[y]]) swap(x,y);
        upgrade_3(id[top[x]],id[x],1,value);
        x=f[top[x]];
    }
    if (id[x]>id[y]) swap(x,y);
    upgrade_3(id[x],id[y],1,value);
}
int query(int l,int r,int num)
{
    if (a[num].l>=l && a[num].r<=r) return a[num].sum;
    pushdown(num);
    int mid=(a[num].l+a[num].r) /2,tot=0;
    if (mid>=l) tot+=query(l,r,num*2);
    if (mid<r) tot+=query(l,r,num*2+1);
    return tot%mod;
}
int sum(int x,int y)
{
    int ans=0;
    while (top[x]!=top[y])
    {
        if (depth[top[x]]<depth[top[y]]) swap(x,y);
        ans=(ans+query(id[top[x]],id[x],1))%mod;
        x=f[top[x]];
    }
    if (id[x]>id[y]) swap(x,y);
    return (ans+query(id[x],id[y],1))%mod; 
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&r,&mod);
    memset(first,-1,sizeof(first));
    for (i=1;i<=n;i++) scanf("%d",&dis[i]);
    for (i=1;i<=n-1;i++) 
    {
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    cnt=0,dfs1(r),dfs2(r,r);
    build(1,n,1);
    for (i=1;i<=m;i++)
    {
        scanf("%d",&op);
        switch(op)
        {
            case 1:scanf("%d%d%d",&x,&y,&z),upgrade_1(x,y,z);break; 
            case 2:scanf("%d%d",&x,&y),printf("%d\n",sum(x,y));break;
            case 3:scanf("%d%d",&x,&z),upgrade_3(id[x],id[x]+size[x]-1,1,z);break;
            case 4:scanf("%d",&x),printf("%d\n",query(id[x],id[x]+size[x]-1,1));break;
        }
    }
    return 0;
}