平衡树treap、splay以及 懒人版平衡树
到目前为止,平衡树应该是我学过的数据结构里面最难的一个了。(顺便贴上一个我认为treap讲解的比较好的博客https://blog.csdn.net/u014634338/article/details/49612159)
此篇博客只会讲解treap平衡树中较为关键的操作。
前情提要
siz:这里的含义是节点u以下含u有多少数的个数
son[][]:第一维表示当前点,第二维记录当前点的左孩子和右孩子
cnt:储存在节点u中,相同元素的数的个数
key:数据给定的值
ran:随机值(主要用于堆操作)
插入

void insert(int &k,int x) { if (k==0) { k=++num; cnt[k]=1; key[k]=x; ran[k]=rand(); siz[k]=1; return; } else if (key[k]==x) { cnt[k]++; siz[k]++; return; } int op=(x>key[k]); insert(son[k][op],x); if (ran[son[k][op]]<ran[k]) rotate(k,!op); pushup(k); }
插入操作一开始先在树里面递归找有没有相同的点,如果有,直接相同元素的个数+1;如果没有,再到叶子节点里面加上去,但是如果直接这么加了的话,树很容易会退化成链,于是这时候要借鉴堆的性质了。堆的形状十分“平衡”,相对于一颗什么都没优化过的树。由于我们都给了结点一个随机值,所以我们按照这个随机值来进行堆操作(大根堆小根堆都行),但是问题来了,堆和平衡树的性质不会有冲突吗?有冲突确实。以小根堆为例,一个左右都比根大,另一个左小右大,那怎么能够把两者的性质结合在一起呢?
(以下图解由开头推荐博客里面引用,侵删)
先来看看图解:
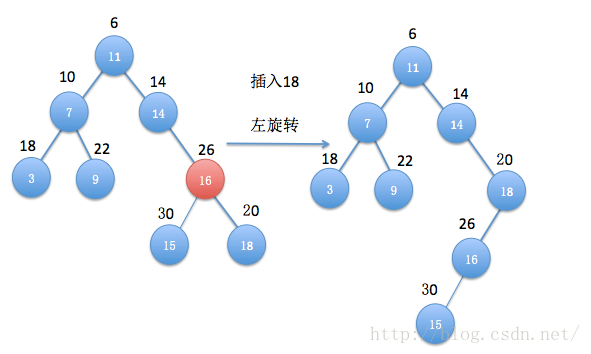
插入值为18,优先级为20的结点后,违反了最小堆的定义,因此要进行调整,把优先级小的往上提,也就是小的优先级插入的是右子树,那么需要进行左旋转,这里进行一次旋转过后就OK了。

同样,这种情况左旋转,旋转后发现还是不满足最小堆的定义,并且小优先级的结点在左子树,所以还需要进行右旋转,如下图所示:

右旋后,很遗憾还是不行,还需要左旋:

OK,终于完成,插入一个数据,也许要进行多次旋转,不过也仅仅是左旋或者右旋而已。
我们由此看到当我们要把两者精华揉在一起时,关键的关键,即是旋转操作,既能维护堆,又能维护平衡树。但是一开始,笔者想到一个问题,仅仅用rand函数随机出来一个值来做为维护堆的依据,是不是有点太草率了,难道不会因为种种原因,而导致随机出来的值特别的奇怪?运行时间不就有不确定性?
以洛谷模板题3369为例,可见每次运行时间只在320ms左右,还算是可以接受的。
删除
分3种情况:
1 不存在这个数,结束
2 存在这个数,而且不止一个,直接递归寻找,然后cnt数组减1
3 存在这个数,但是只有一个,那么这个时候就很烦人了。需要经过一系列的左旋右旋操作,把此结点扔到叶子节点的位置,然后删掉。那么问题来了,如果这个点同时拥有左孩子和右孩子,什么时候左旋什么时候右旋呢?前面我们有介绍了随机值这个东西来维护堆,我们如果要删去一个结点,就一定要让这棵树始终保持堆的性质,因此我们在考虑左旋还是右旋时,先比较两者的随机值的大小,以小根堆为例,如果左边的随机值比右边的小,那么左孩子就应该与当前要删去的结点换一个位置,即左旋,在把删去的结点扔到更下一层的同时,保证了堆和平衡树的性质。

void _delete(int &k,int x) { if (k==0) return; if (x!=key[k]) { int op=(x>key[k]); _delete(son[k][op],x); pushup(k); return; } if (cnt[k]>1) { cnt[k]--; siz[k]--; pushup(k); return; } if (!son[k][0]&&son[k][1]) { rotate(k,0); _delete(son[k][0],x); } else if (son[k][0] && !son[k][1]) { rotate(k,1); _delete(son[k][1],x); } else if (!son[k][0] && !son[k][1]) { cnt[k]--; siz[k]--; if (cnt[k]==0) k=0; } else { int op=(ran[son[k][0]]>ran[son[k][1]]); rotate(k,!op); _delete(son[k][!op],x); } pushup(k); }
旋转

void rotate(int &x,int op) { int p=son[x][!op]; son[x][!op]=son[p][op]; son[p][op]=x; pushup(x); pushup(p); x=p; }
这个大多数博客都有讲,而且把其视为最重要的操作,其实在我看来,我们只要把旋转操作视为交换两个点的位置就行,只不过由于是颗平衡树,交换位置会导致“牵一发而动全身”,才显得比较复杂。这里就不再过多阐述旋转的操作。
总结
平衡树花了我很多时间去学习,可能是由于每个人码风不同,或是我认为的难点大多数博主都一笔带过,学习的过程就有点艰苦......。但是当你完全理解之后,才会体会到平衡树的魅力。
最后附上洛谷模板题的代码(因为我是靠看别人的代码来逐渐弄懂的,所以可能和别人的代码有点雷同)

#include <bits/stdc++.h> #define maxn 1000010 #define inf 0x3f3f3f3f using namespace std; int key[maxn],cnt[maxn],ran[maxn],siz[maxn],son[maxn][2],op,n,num=0,x,root=0; void pushup(int x) { siz[x]=siz[son[x][0]]+siz[son[x][1]]+cnt[x]; } void rotate(int &x,int op) { int p=son[x][!op]; son[x][!op]=son[p][op]; son[p][op]=x; pushup(x); pushup(p); x=p; } void insert(int &k,int x) { if (k==0) { k=++num; cnt[k]=1; key[k]=x; ran[k]=rand(); siz[k]=1; return; } else if (key[k]==x) { cnt[k]++; siz[k]++; return; } int op=(x>key[k]); insert(son[k][op],x); if (ran[son[k][op]]<ran[k]) rotate(k,!op); pushup(k); } void _delete(int &k,int x) { if (k==0) return; if (x!=key[k]) { int op=(x>key[k]); _delete(son[k][op],x); pushup(k); return; } if (cnt[k]>1) { cnt[k]--; siz[k]--; pushup(k); return; } if (!son[k][0]&&son[k][1]) { rotate(k,0); _delete(son[k][0],x); } else if (son[k][0] && !son[k][1]) { rotate(k,1); _delete(son[k][1],x); } else if (!son[k][0] && !son[k][1]) { cnt[k]--; siz[k]--; if (cnt[k]==0) k=0; } else { int op=(ran[son[k][0]]>ran[son[k][1]]); rotate(k,!op); _delete(son[k][!op],x); } pushup(k); } int rank(int k,int x) { if (k==0) return 0; if (key[k]==x) return siz[son[k][0]]+1; if (key[k]>x) return rank(son[k][0],x); return siz[son[k][0]]+cnt[k]+rank(son[k][1],x); } int find(int k,int x) { if (k==0) return 0; if (siz[son[k][0]]>=x) return find (son[k][0],x); else if (siz[son[k][0]]+cnt[k]<x) return find (son[k][1],x-siz[son[k][0]]-cnt[k]); else return key[k]; } int lowerbound(int k,int x) { if (k==0) return -inf; if (key[k]>=x) return lowerbound(son[k][0],x); else return max(key[k],lowerbound(son[k][1],x)); } int upperbound(int k,int x) { if (k==0) return inf; if (key[k]<=x) return upperbound(son[k][1],x); else return min(key[k],upperbound(son[k][0],x)); } int main() { cin>>n; while (n--) { scanf("%d%d",&op,&x); switch(op) { case 1:insert(root,x);break; case 2:_delete(root,x);break; case 3:printf("%d\n",rank(root,x));break; case 4:printf("%d\n",find(root,x));break; case 5:printf("%d\n",lowerbound(root,x));break; case 6:printf("%d\n",upperbound(root,x));break; } } return 0; }
splay
相较于treap来说,splay不需要任何额外的内容,只要保证一个splay和旋转的操作即可,而所谓的splay操作,就是通过旋转把一个点向上转到目标点的操作。
模板:https://blog.csdn.net/clove_unique/article/details/50636361
懒人版平衡树
其实C++STL基本容器里面有很多好东西,常见的就是vector、set、map等等,这里用到的是vector来实现平衡树功能

代码极短

#include <bits/stdc++.h> #define debug freopen("r.txt","r",stdin) #define mp make_pair #define ri register int using namespace std; typedef long long ll; typedef pair<int, int> pii; const int maxn = 4e5+5; const int INF = 0x3f3f3f3f; const int mod = 998244353; inline ll read(){ll s=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w;} ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;} vector<int>v; int t,opt,x; int main() { t=read(); while(t--) { opt=read(),x=read(); if(opt==1) v.insert(lower_bound(v.begin(),v.end(),x),x); if(opt==2) v.erase (lower_bound(v.begin(),v.end(),x)); if(opt==3) printf("%d\n",lower_bound(v.begin(),v.end(),x)-v.begin()+1); if(opt==4) printf("%d\n",v[x-1]); if(opt==5) printf("%d\n",v[lower_bound(v.begin(),v.end(),x)-v.begin()-1]); if(opt==6) printf("%d\n",v[upper_bound(v.begin(),v.end(),x)-v.begin()]); } return 0; }
但是可能会被卡数据




