新生赛中大
根据新生赛题解文件编写,目的最主要是记录一下我第一次正式的参加ACM比赛,其间学到了挺多的,也感受到自己与外校的人的差距之大,慢慢努力吧。
A、B水题。
C 给你一个三角形(三个点的坐标),你要用一条与x轴垂直的直线x=x0将三角形分成面积相等的两个部分,输出x0。
我的做法:二分,结果不知具体原因WA了,只能乖乖送人头。
题解:先排序,设x1<=x2<=x3,计算出:
当x2*2>=x1+x3时,答案为x1+sqrt(0.5*(x2-x1)*(x3-x1))
当x2*2<=x1+x3时,答案为x3-sqrt(0.5*(x3-x2)*(x3-x1))
看不懂,逃......。
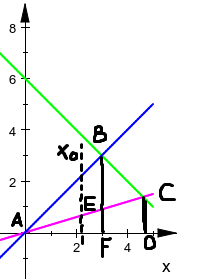
求助了朋友,算是懂了那么一点点,先从特殊情况处理,(0,0)是(x1,y1),(2.5,2.5)是(x2,y2),(8,0)是(x3,y3)。
(图画的不好)
蓝色线斜率为k,则x0*kx0*1/2=1/2(x3*kx2*1/2);得x0=sqrt(x2*x3*0.5);
再推导,
(E点是BF交于粉线的那个点)
可判断x0是要交于蓝粉这两条线的,设蓝线斜率为k1,粉线k2,
则0.5*x0*k1*x0-0.5*x0*k2*x0=0.5(0.5*x3*k1*x2+0.5*k2*x3*(x3-x2)-0.5*k*x3*x3)
0.5*Sabc=0.5(Sabd+Sbcd-Sacd)
Sabd+Sbcd-Sacd=Sabc 成立
再把0.5*x0*k1*x0-0.5*x0*k2*x0=0.5(0.5*x3*k1*x2+0.5*k2*x3*(x3-x2)-0.5*k*x3*x3)化简
得x0=sqrt(x2*x3*0.5);
再推导:
我们可以想象一下,如果整个三角形平移一下,那么x1的坐标就不再是0.于是
这条公式就变成(x0-x1)=sqrt((x2-x1)*(x3-x1)*0.5),相当于把平移了x1个距离的三角形再挪回类似上图一样的位置。
同理可证当x2*2<=x1+x3时的情况。
D 给出三条线的A B C,即Ax+By+C=0,算三条线能划分为几个区域
这题队友说高中时写过,但是我忘了,只能交由他来写,但是可能坑比较多,导致又送一人头。
题解:
分类讨论题,分七种情况:
1、三条直线重合,答案为2
2、只有两条直线重合,且和第三条平行,答案为3
3、只有两条直线重合,且和第三条相交,答案为4
然后以下都是没有重合的:
4、三条直线平行,答案为4
5、两条直线平行,且和第三条相交,答案为6
6、三条直线交于三点,答案为7
7、三条直线交于一点,答案为6
额,可能浮点数什么的比较烦,或者判断条件可能有点特殊,导致WA了吧
E 给n个物品,物品可以分为两类,一类价格(P)相同,一类价值(H)相同,在某个价格之内选出m个物品使得价值最大,输出价值。
我的做法:这不是背包吗?但是一看价格和价值范围1e9,逃,放弃。
题解:
P相同的,肯定优先选H大的
H相同的,肯定优先选P小的
分别排序后,对P相同的那些求H的前缀和,然后枚举H相同的选多少个,然后直接算出P相同的选多少个,直接算出答案
额,题解说是01背包,我更感觉像道十分巧妙的智商题,想到前缀和之后应该可以很快能做出这题来了,哎,看来惯性思维的问题对于我而言有点严重,看到价值、最优的字眼就抓着经典背包问题不放,题目还是做的有点少啊。
F 给你一个数x,每次把x变成x-1或者x最大质因数,问至少多少次能变成0
我的做法:可喜可贺在WA3次之后做出了这题。我是先把素数表给打出来,然后一个一个素数( i )来乘以1~ ∞ ( j ),如果i*j 小于 1e5 (题目的范围,比较小所以不用担心超时),那么用数组把数 i*j 标记为 i 说明这个数当前的最大质因数是 i ,因为是从小到大扫过去,所以不必担心找不到最大质因数,因为小的会被大的给覆盖掉。如果 i*j 大于 1e5 就退出。之后就像跳棋一样不断跳到当前值的最大质因数,记录步数就可以了。
题解: 分解质因数,然后DP即可。 注意分解质因数需要使用𝑂(√𝑛)的复杂度。
好像差不多,AC了就行。
G 给你一个序列,问对这个序列进行重排后最多能有多少个 在相同位置有不同的值
我的看法(是看法不是做法,赛场上看到少人做就没想这题了):应该先要记录每个数出现的个数然后再用某个算法来做,乖乖放弃这题。
题解:显然这个答案和这个序列里的众数有关。
如果众数数量num大于序列长度的一半(n/2),
那么答案就是(n-num)*2 否则答案就是n
数据范围要求我们只能使用O(n)的算法来做,使用数字打架的算法来得出的数,要么是出现次数超过一半的数字,要么可以是任意一个数字,得出的数字我们再次检查它的出现次数即可。
数字打架:用抵消的思想,如果出现相同的数字我们把次数加一,否则减一,如果减成负数,那么当前保留的数字换成这个不同的数字,次数赋值为1。
数字打架?活到老,学到老。
H 有n杯饮料,每杯饮料有s_i种配料,饮料的价值由它里面的配料当中最小的值决定,每一点能量可以使得某一配料的价值上升1,要使得所有饮料价值和上升m,问最少要花多少体力
我的看法:无,逃.......
题解:优先队列,这题可以留着应该可以想出来。
I 有n堆豆子,两个人轮流操作,每次必须要取最左边的未被取完的那堆豆子。问先手最多能比后手多取几个。
我的看法:博弈?不懂。
题解:
方法一:贪心
你可以始终让先手占有决定权,通过判断之后的1的个数为奇数还是偶数来决定本回合你是否要留一个1.
special case:如果一开始的几个是1,将交换先后手。
方法二:动态规划
从后往前来计算从第i堆到第n堆豆子,先手最多可以赢后手多少个豆子,f[1][0]-f[1][1]即为答案
if(ai>1) f[i][0]=max(f[i+1][0]+a[i]-1,f[i+1][1]+a[i]), f[i][1]=sum-f[i][0];
else f[i][0]=f[i+1][1]+1, f[i][1]=f[i+1][0];
这类题目我已经安排好用一段时间去死磕了,我自己对这种两个人在那对决看谁赢的题目感觉到真的有心无力,看起来好像很简单,但是又无从下手的样子,希望刷多点这种题来补救一下吧。
J 给你一棵树,两个人A,B在上面,每个人往父亲节点爬一步消耗一点体力。 A和B不能在同一个点,当B在A上方时,A可以不花体力把B扔到B的父亲节点。 问两个人的体力和最小是多少。
我的做法:这题在比赛快结束时才看然后想出来的,真就算是个裸的LCA,因为体力要最小,所以只要求出两点的最近公共祖先,然后直接把两个点的深度一加再减去LCA的深度差不多答案就出来了,白给一题,当作交学费吧。
题解:求两人深度,求LCA(解释)深度,ans=两人深度-LCA深度-1。
special case: A是B父亲时,ans=两人深度-1。
比赛之后,LCA我也重新写了一遍,感受到树上倍增这个思想是真的精妙。
K 问n×m的网格图中,有多少弹球的起始方案(位置+方向)可以回到起始状态。
我的看法:看题,嗯,很好,是个好题,下一道......
题解:如果一个方案不能回到起始状态,球最终一定去了角落。那么从角落出发开始遍历这个图,统计一下不能回到起始状态的方案数,用总方案数减掉得到答案。
答案:(𝑛−2)∗(𝑚−2)∗4+((𝑛−2)∗2+(𝑚−2)∗2)∗2+4−𝑙𝑐𝑚(𝑛−1, 𝑚−1)∗4 不懂,逃
L 有一个𝑛×𝑚的棋盘,棋盘上有障碍物和洞,现在要将球移到洞里,每一步可以将球往四个方向之一滚,球会一直滚直到碰到边界或者障碍,或者经过洞掉下去,问最少需要多少步才能把球移到洞内。
我的看法:路径压缩后建图吗?其实赛场上我是感觉可以开这题的。
题解:由于棋盘太大,所以不能把整个棋盘记下来,只能记住有效位置(球会停下来的位置),显然有效位置就是棋盘的四周边界以及障碍物相邻的四个格子,将有效位置离散化,构成一个有向图,跑一次bfs(宽度优先搜索)就能得到答案。
M 有若干个人需要升级,升级需要消耗一些材料,材料有一个合成系统,合成系统构成一个DAG(有向无环图),只有没有出度的材料(基础材料)才能通过刷副本拿到,刷一次副本能拿到两种基础材料,并花费一定体力值,问把所有人都升级最少需要多少体力值。 题目最后一部分意思:如果将每个基础材料看成点,副本看成边,那么构成的图只有链。
题解:首先拓扑排序,算出每种基础材料需要多少个,然后把每条链找出来,对于每条链DP(动态规划)求出答案。 𝑓[𝑖][𝑗]表示前𝑖−1个基础材料已经满足需求,第𝑖个基础材料拿到至少𝑗个,需要的最少体力值。




