终极模板“水题”——网络流

其实这篇https://www.cnblogs.com/victorique/p/8560656.html写得很完整了，但是为了加深自己的印象，就自己写一篇吧。

 

网络流的练习我用了传说中的网络流24题，我把题目都看了一遍，发现一个问题，有些题好像真的是为了网络流而搞网络流的做法出来，导致题目的可做性不强，虽然如此，但是除了这些题目之外，其他的题目，也挺让我耳目一新的。

其实，网络流把两套模板给记住，基本上就算是完成了一道题的一大半了。第一套模板是网络最大流（dinic+当前弧优化）；第二套模板是最小费用最大流（利用spfa找出最短路的同时保证网络最大流）但是如果像我这么说的话，把网络流单纯看成模板题，是肯定是做不出来题目的，那么网络流关键的点在哪？网络流通常的套路又是什么？

1.建图

基本上网络流的题都难在这里了。如何建图，是一个难点。

（1）二分图

 

一类建图即是以二分图的形式来建，其包括操作拆点，建立超级源点、汇点，等等。那么在二分图上，能进行解决什么问题呢？最普遍的莫过于匹配问题，通过二分图，求出点与点之间的最大匹配值，然后再利用二分图上的性质，来求出问题的解，而二分图上的性质有下面几种常用的：最大匹配=最小点覆盖；最小路径覆盖=|G|-最大匹配数（G为点数）；最大独立集=点数-最大匹配=最小边覆盖。我们可以看到求出一个最大匹配，基本上就能算出其他的问题出来，大多数问题也是基于二分图原理来问的。

例题有：飞行员配对方案问题，试题库问题等，

 还有一种类似与二分图的建图方法，其特点是可以从右边的点再回去左边的点，有点像路径问题，但是也不全是，把图画出来其实也大概是上面那个图的模样，应该算是一个变种吧。

例题：数字梯形问题的第一问

（2）普通图

 

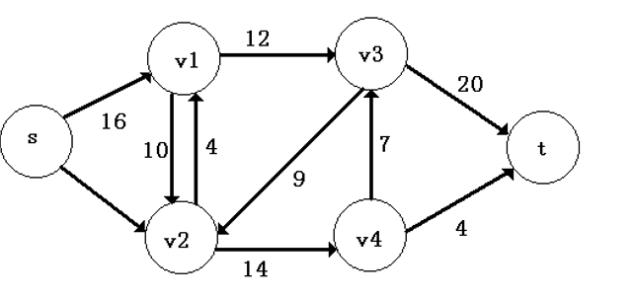
这种图就不说了，应该是网络流题目里面最基础的图。

 （3）序列上的图

 

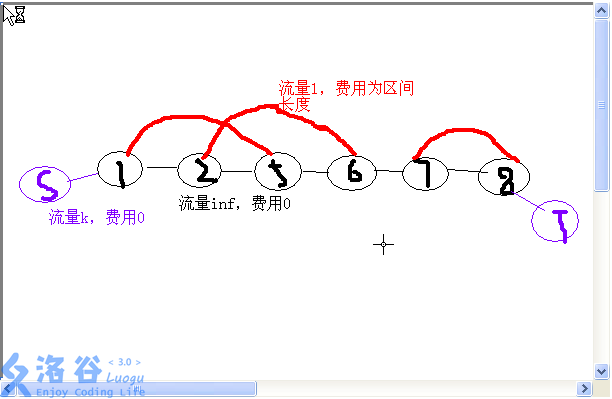
 （侵删）

这些题并不类似于我们平时做的网络流题，它是在序列上的，且很难建出来二分图，因此只能让它待在序列上。由于只接触了一道这种题目，而且还是不太理解的那种，这里就只给出一道例题来参考。

例题：最长k可重区间集问题

2.网络流的模型

最小割，最小费用最大流，最大费用最大流等等。

总结：刷最大流题目，首先懂得要怎么去建图，把图建好，套上模板，基本上不会出大问题，这里我留下一个疑问，这是我在某个题解的评论里面看到的，原话是：费用流能解决所有线性规划问题，不知是真是假......

 

费用流模板

#include <bits/stdc++.h>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int maxn = 4e5+5;
const int INF = 2147483647; 
const int mod = 998244353;
const int N=500005;//点 
const int M=500005;//边 
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}

int top;
int pre[N];
ll dist[N];
bool vis[N];
int c[N];
int maxflow;

struct Vertex
{
    int first;
}V[N];

struct Edge
{
    int v,next;
    int cap,flow,cost;
}E[M];

void init()
{
    memset(V,-1,sizeof(V));
    top=0;
    maxflow=0;
}

void add_edge(int u,int v,int c,int cost)
{
    E[top].v=v;
    E[top].cap=c;
    E[top].flow=0;
    E[top].cost=cost;
    E[top].next=V[u].first;
    V[u].first=top++;
}

void add(int u,int v,int c,int cost)
{
    add_edge(u,v,c,cost);
    add_edge(v,u,0,-cost);
}

bool SPFA(int s,int t,int n)
{
    int i,u,v;
    queue<int>qu;
//    for (i=1;i<=n+1;i++) vis[i]=false;
//    for (i=1;i<=n+1;i++) c[i]=0;
//    for (i=1;i<=n+1;i++) pre[i]=-1;
    memset(vis,false,sizeof(vis));
    memset(c,0,sizeof(c));
    memset(pre,-1,sizeof(pre));
    for(i=1;i<=n;i++) dist[i]=INF;
    vis[s]=true;
    c[s]++;
    dist[s]=0;
    qu.push(s);
    while(!qu.empty())
    {
        u=qu.front();
        qu.pop();
        vis[u]=false;
        for(i=V[u].first;~i;i=E[i].next)
        {
            v=E[i].v;
            if(E[i].cap>E[i].flow&&dist[v]>dist[u]+E[i].cost)
            {
                dist[v]=dist[u]+E[i].cost;
                pre[v]=i;
                if(!vis[v])
                {
                    c[v]++;
                    qu.push(v);
                    vis[v]=true;
                    if(c[v]>n) return false;
                }
            }
        }
    }
    if (dist[t]==INF) return false;
    return true;
}
ll MCMF(int s,int t,int n)
{
    int d;
    int i;
    ll mincost=0;
    while(SPFA(s,t,n))
    {
        d=INF;
        for(i=pre[t];~i;i=pre[E[i^1].v])
        {
            d=min(d,E[i].cap-E[i].flow);
        }
        maxflow+=d;
        for(i=pre[t];~i;i=pre[E[i^1].v])
        {
            E[i].flow+=d;
            E[i^1].flow-=d;
        }
        mincost+=dist[t]*d;
    }
    return mincost;
}
int T,n,m,s,t;
int main()
{
  先init，再add建图，然后直接ans=MCMF(s,t,t+1);
  即可得出最大流和最小费用  
}

 最大流模板（更高级的ISAP）

#include <bits/stdc++.h>
#define debug freopen("r.txt","r",stdin)
#define mp make_pair
#define ri register int
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int maxn = 4e5+5;
const int INF = 0x3f3f3f3f; 
const int mod = 998244353;
const int N=500005;//点 
const int M=500005;//边 
inline ll read(){ll s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;}
ll qpow(ll p,ll q){return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
struct FLOW{ //ISAP最大流
    struct edge{int to,w,nxt;}; //指向，限流，下一条边
    vector<edge> a; int head[N]; //前向星 
    int cur[N]; //当前弧 
    int n,s,t; //点数，源点，汇点
    queue<int> q;
    int dep[N],gap[N]; //gap[x]为等于x的dep[i]的个数
    void ae(int x,int y,int w){
        a.push_back((edge){y,w,head[x]});
        head[x]=a.size()-1;
    }
    bool bfs(){ //记录dep和gap
        fill(dep,dep+n,-1); dep[t]=0;
        fill(gap,gap+n,0); gap[0]=1;
        q.push(t);
        while(!q.empty()){
            int x=q.front(); q.pop();
            for(int i=head[x];i!=-1;i=a[i].nxt){
                int p=a[i].to;
                if(dep[p]!=-1)continue;
                dep[p]=dep[x]+1;
                q.push(p);
                gap[dep[p]]++;
            }
        }
        return dep[s]!=-1;
    }
    int dfs(int x,int fl){ //多路增广
        int now,ans=0;
        if(x==t)return fl;
        for(int i=cur[x];i!=-1;i=a[i].nxt){ //当前弧开始（可以不重复访问废边）
            cur[x]=i; //记录当前弧
            int p=a[i].to;
            if(a[i].w && dep[p]+1==dep[x])
            if((now=dfs(p,min(fl,a[i].w)))){
                a[i].w-=now;
                a[i^1].w+=now;
                ans+=now,fl-=now; //流量更新
                if(fl==0)return ans;
            }
        }
        gap[dep[x]]--;
        if(gap[dep[x]]==0)dep[s]=n;
        dep[x]++;
        gap[dep[x]]++;
        return ans;
    }
    void init(int _n){ //初始化
        n=_n+1;
        a.clear();
        fill(head,head+n,-1);
    }
    int solve(int _s,int _t){ //返回最大流
        s=_s,t=_t;
        int ans=0;
        if(bfs())
        while(dep[s]<n){
            copy(head,head+n,cur); //当前弧初始化
            ans+=dfs(s,INF);
        }
        return ans;
    }
}flow;
#define add(x,y,w) flow.ae(x,y,w),flow.ae(y,x,0)
//先flow.init(n)，再add添边，最后flow.solve(s,t)
int main()
{
    int n,m,s,t,u,v,w;
    n=read(),m=read(),s=read(),t=read();
    flow.init(n);
    for (int i=1;i<=m;i++)
    {
        u=read(),v=read(),w=read();
        add(u,v,w);
    }
    cout<<flow.solve(s,t);
    return 0;
}