题解[T200448 Call of The Void]
题意:
设 \(g(n)=\varphi(n)\sum\limits_{d^2|n}\mu(\frac{n}{d^2})\) ,\(\operatorname{dis}(x,y)=\prod\limits_{i\in path(x,y)}a_i\)
求 \(\prod\limits_{i=1}^{n}\prod\limits_{j=i+1}^{n}g(\operatorname{dis}(x,y))\)
\(\text{Part 1}\) : 推式子
首先那个 \(\sum\limits_{d^2|n}\mu(\frac{n}{d^2})\) 先可以化简:
\(\sum\limits_{d^2|n}\mu(\frac{n}{d^2})\)=\(\sum\limits_{d|n}\mu(\frac{n}{d})[d=k^2,k\in N^+]\)
卷积中的两个函数皆为积性函数,直接狄利克雷生成函数上:
\(=[n^{-z}]\left(\prod\limits_{p\in\text{Prime}}1-\dfrac{1}{p^z}\right)\left(\prod\limits_{p\in\text{Prime}}\sum\limits_{i\geq0}\dfrac{1}{p^{2iz}}\right)\)
\(=[n^{-z}]\left(\prod\limits_{p\in\text{Prime}}1-p^{-z}\right)\left(\prod\limits_{p\in\text{Prime}}\dfrac{1}{1-p^{-2z}}\right)\)
\(=[n^{-z}]\prod\limits_{p\in \text{Prime}}\dfrac{1}{1+p^{-z}}\)
\(=[n^{-z}]\prod\limits_{p\in\text{Prime}}\sum\limits_{i\geq0}\dfrac{(-1)^i}{p^{iz}}\)
所以可得 \(\sum\limits_{d^2|n}\mu(\frac{n}{d^2})=(-1)^{f(n)}\) 其中 \(f(n)\) 代表 \(n\) 的质因子次幂的和。
而这就是刘维尔函数,即 \(\sum\limits_{d^2|n}\mu(\frac{n}{d^2})=\lambda(n)\)
所以 \(g(n)=(-1)^{f(n)}\varphi(n)=(-1)^{f(n)}n\prod\limits_{p\in\text{Prime},p|n}1-\frac{1}{p}\)
由于 \((-1)^{f(n)}\) 与 \(n\) 都是完全积性函数。
这两者只需统计出每个点有多少条路径经过,再快速幂计算贡献。
关键就是 \(\prod\limits_{p\in\text{Prime},p|n}1-\frac{1}{p}\)
由于最终的答案还要乘上所有不同路径的点权积的这个值的积。
可以考虑每个质数 \(p\) 在树中有多少条路径包含。
那每个 \(p\) 的贡献就是 \(1-\frac{1}{p}\) 的这个路径数次方。
这明摆着就是要建虚树求,考虑如何 \(\text{dp}\)。
\(\text{Part 2}\) : \(\text{dp}\)
虚树上由关键点与辅助点构成,需分开讨论。
设 \(size(z)\) 是 \(x\) 在原树上的子树大小。
再设 \(sz(x)=\text{x}\) 子树内离 \(\text{x}\) 最近的关键点的子树大小之和。
特别的,\(\text{x}\) 自己是关键点时 \(sz(x)\) 就是 \(size(x)\) 。
举个例子:
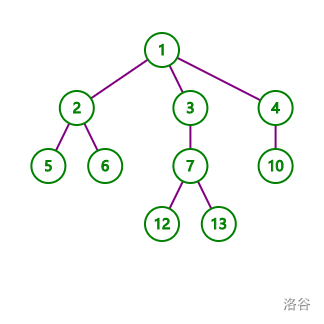
若 \(2,4,6,12,13\) 为关键点。
虚树上的点与其 \(sz\) 即为 \(sz_1=7,sz_2=3,sz_4=sz_7=2,sz_6=sz_{12}=sz_{13}=1\)
假定在 \(\text{dp}\) 时要处理出来以每个点为 \(lca\) 的路径个数,以及每个点到其虚树上的儿子上不在虚树中的点的贡献。
设当前处理的点为 \(x\) 。
若 \(x\) 为关键点
其子树内经过 \(x\) 的在其子树内的路径皆合法,这可以提前预处理出。
而对于它每个虚树上的儿子 \(y\) , \(x\) 到 \(y\) 上的不在虚树中的节点都能与 \(sz(y)\) 所代表的点产生贡献。
设 \(y\) 是 \(x\) 在原树上 \(x\) 的儿子 \(z\) 中的子树, \(z\) 可以倍增求出。
则此部分贡献就是 \(sz(y)\times(size(z)-size(y))\)
若 \(x\) 为辅助节点
考虑每个 \(x\) 在树上的节点 \(y\) 的 \(sz\) 能与其它点的贡献。
首先 \(sz(y)\) 能乘上搜到 \(y\) 之前全部子节点的 \(sz\) 和,明确搜到 \(y\) 之前是为了不算重。
这样算出来的路径上关键点个数都 \(\geq 2\)。
除此之外,每个 \(sz(y)\) 还能与其他 \(x\) 子树中到 \(x\) 路径上无关键点的点产生贡献。
其为 \(v=size(x)-\sum\limits_{y\in son(x)}sz(y)\) ,此处 \(y\) 为虚树上 \(x\) 的儿子。
由于 \(size(y)-sz(y)\) 这些点理应在处理 \(y\) 时与 \(sz(y)\) 算过。
所以这部分贡献是 \(sz(y)\times (v-size(y)+sz(y))\)
时间复杂度
对于每个点的权值,会算其质因子个数次,虚树总点数约为 \(O(n\dfrac{\ln V}{\ln\ln V})\)
证明可参考 这里
再加上预处理以及建虚树、倍增的时间复杂度。
总时间复杂度为 \(O(V+n\log n\dfrac{\ln V}{\ln\ln V})\)
代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10,V=1e6,mod=998244353;
int n,m,x,y,z,tot,tt,l,dl,tp;char ch,lambda[V+10];
int a[N],fd[N],p[V+10],prm;ll res,ans,qres,v,inv[V+10],wp[V+10];
int to[N<<1],nextn[N<<1],h[N],edg;bool b[V+10],bb[N];
int dfn[N],tmp[N],st[N];int ff[N][20],dep[N];ll size[N],sz[N],sum[N];
int to1[N],nextn1[N],h1[V+10],edg1;
inline void read(int &x){
x=0;ch=getchar();while(ch<48||ch>57)ch=getchar();
while(ch>47&&ch<58)x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
}
void write(int x){if(x>9)write(x/10);putchar(48+x%10);}
void init(){
register int i,j;
lambda[1]=1;
for(i=2;i<=V;++i){
if(!b[i])p[++prm]=i,lambda[i]=-1;
for(j=1;j<=prm&&(x=i*p[j])<=V;++j){
b[x]=1;
lambda[x]=-lambda[i];
if(i%p[j]==0)break;
}
}
inv[1]=1;
for(i=2;i<=V;++i)inv[i]=(mod-mod/i)*inv[mod%i]%mod;
for(i=1;i<=prm;++i)wp[i]=(mod+1-inv[p[i]])%mod;
}
inline void qpow(ll x,ll k){
qres=1;
while(k){
if(k&1)qres=qres*x%mod;
x=x*x%mod;
k>>=1;
}
}
void init(int x,int anc){
ll v=0;
int i,y;dfn[x]=++tt;ff[x][0]=anc;dep[x]=dep[anc]+1;
for(i=1;i^19;++i)ff[x][i]=ff[ff[x][i-1]][i-1];size[x]=1;
for(i=h[x];y=to[i],i;i=nextn[i])if(y^anc){
init(y,x);
v+=size[x]*size[y];
size[x]+=size[y];
}
sum[x]=v;
v+=size[x]*(n-size[x]);
h[x]=0;
if(lambda[a[x]]^1&&v&1)res=mod-res;
qpow(a[x],v);ans=ans*qres%mod;
}
bool cmp(int a,int b){return dfn[a]<dfn[b];}
inline void lca(int x,int y){
register int i;
if(dep[x]<dep[y])x^=y^=x^=y;
for(i=19;~i;--i)if(dep[ff[x][i]]>=dep[y])x=ff[x][i];
if(x==y)l=x;
else {
for(i=19;~i;--i)if(ff[x][i]^ff[y][i])x=ff[x][i],y=ff[y][i];
l=ff[x][0];
}
}
inline void add(int x,int y){to[++edg]=y,nextn[edg]=h[x],h[x]=edg;}
inline void add1(int x,int y){to1[++edg1]=y,nextn1[edg1]=h1[x],h1[x]=edg1;}
void find(int x,int y){
register int i;dl=dep[y]+1;
for(i=19;~i;--i)if(dep[ff[x][i]]>=dl)x=ff[x][i];
z=x;
}
void dfs(int x){
int i,y;
if(bb[x]){
for(i=h[x];y=to[i],i;i=nextn[i]){
dfs(y);find(y,x);
res+=sz[y]*(size[z]-size[y]);
}
res+=sum[x];
sz[x]=size[x];
}
else {
sz[x]=0;ll v=0;
for(i=h[x];y=to[i],i;i=nextn[i]){
dfs(y);v+=sz[y];
res+=sz[y]*sz[x];
sz[x]+=sz[y];
}
v=size[x]-v;
for(i=h[x];y=to[i],i;i=nextn[i])
res+=sz[y]*(v-size[y]+sz[y]);
}
h[x]=0;
}
main(){
read(n);register int i,j,k;init();
for(i=1;i^n;++i)read(x),read(y),add(x,y),add(y,x);
for(i=1;i<=n;++i)read(a[i]),add1(a[i],i);
res=ans=1;init(1,0);edg=0;ll res1=1;
ans=ans*res%mod;
for(i=1;x=p[i],i<=prm;++i){
tot=0;
for(j=x;j<=V;j+=x)for(k=h1[j];k;k=nextn1[k])bb[tmp[++tot]=to1[k]]=1;
if(tot){
sort(tmp+1,tmp+tot+1,cmp);
st[tp=1]=1;
for(j=(tmp[1]==1)+1;x=tmp[j],j<=tot;++j){
lca(x,z=st[tp]);dl=dfn[l];
if(l^z){
--tp;
while(dfn[y=st[tp]]>dfn[l])add(y,z),z=y,--tp;
add(l,z);if(l^y)st[++tp]=l;
}
st[++tp]=x;
}
z=st[tp];--tp;
while(y=st[tp])add(y,z),z=y,--tp;
res=0;dfs(1);
qpow(wp[i],res);
ans=ans*qres%mod;edg=0;
for(j=1;j<=tot;++j)bb[tmp[j]]=0;
}
}
write(ans);
}


