斐波那契树

原题：斐波那契树

\(Description\)：

定义满足下面条件的树是斐波拉契树：

• 这棵树的节点要么是白色，要么是黑色。

• 每一个非叶子的白色节点，有且仅有一个黑色节点作为儿子；每一个非叶子的黑色节点，有且仅有一个黑色节点和一个白色节点作为儿子。

• 根节点为白色节点。

现在给你树的深度\(n\)，每个叶子节点的深度都为\(n\)，问求距离为\(d\)的白色点对一共有多少对？

需要求出\(1\leq d\leq2∗n\)的每一个取值的答案。

\(Input\) \(Format\)

输入仅一行，一个整数nn，表示这个斐波拉契树的深度。

\(Output\) \(Format\)

输出共\(2*n\)个整数，第\(i\)个整数表示当\(d=i\)的时候的答案,答案\(mod 123456789\)

\(Sample\) \(Input\)

5

\(Sample\) \(Output\)

0 2 3 3 1 1 0 0 0 0

\(Solution\)

首先为什么这棵树叫斐波那契树呢

这是一张\(n=6\)的图：

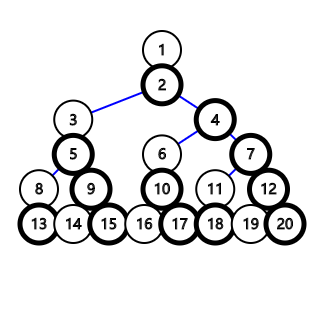
每层黑色与白色的点的个数似乎就是斐波那契数列！

前几个值如下

颜色\层数|\(1\)|\(2\)|\(3\)|\(4\)|\(5\)|\(6\)
:--😐:--😐:--😐:--😐:--😐:--😐:--😐:--:
\(white\)|\(1\)|\(0\)|\(1\)|\(1\)|\(2\)|\(3\)
\(black\)|\(0\)|\(1\)|\(1\)|\(2\)|\(3\)|\(5\)

还有一点，斐波那契树的每棵子树都反复出现在图里！！

那这两个性质怎么用呢？

再分析下题目：

两个点距离为\(d\)的白色节点有两种情况

1.两个点在同一条链上，此时它们的\(lca\)是白色节点

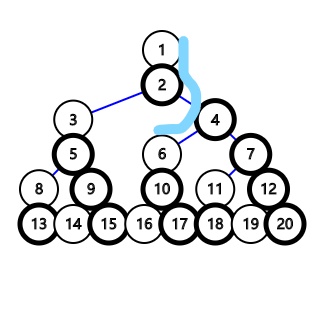
2.两个点距其\(lca\)的和为\(d\)，它们的\(lca\)是黑色节点(与第一种情况没有重复)

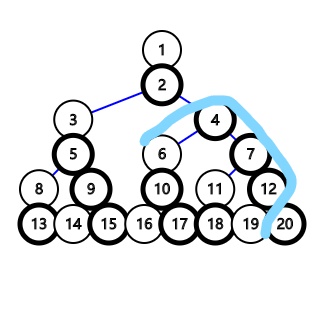
对第一种情况，若枚举可成为两个白色节点的\(lca\)的白色节点的个数与长度，显然是行不通的

这时我们就可以将这一段链迭代到一号节点上去：

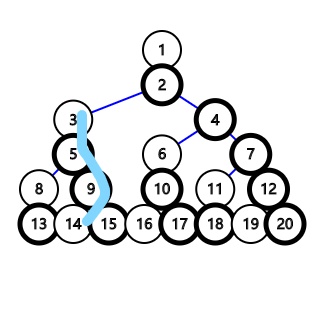
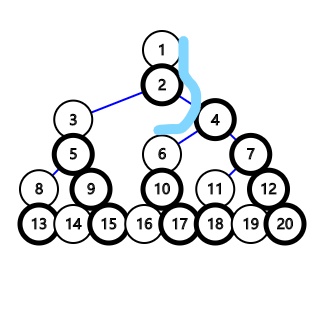
于是长度为\(d\)的点对个数为 可充当上面白色节点的个数*可充当下面白色节点的个数

由于迭代，后者显然是第\(d\)行白色节点的个数

而前者则是\(n-i\)行及之前一共的白色节点的个数

若用\(f[i]\)表示距离为\(i\)的白色点对有多少个

第一种情况时\(f[i]+=sumw[n-i]*w[i+1]\)其中\(sum[k]\)代表在\(k\)行及之前一共的白点数量，\(w[k]\)代表第\(k\)行一共的白点个数

对第二种情况也可以用类似的迭代方法：

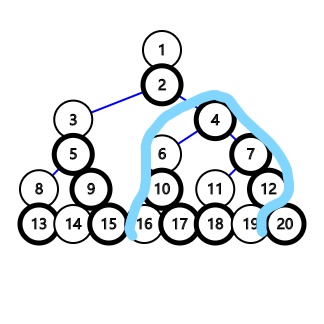
可以将其\(lca\)这个黑节点迭代到二号节点上：

这时我们就可以枚举两个白色节点到其\(lca\)的长度\(i\)和\(j\)

那可以充当两个白色节点的\(lca\)的黑色节点的个数仅有\(n-max(i,j)\)

而对两个白色节点可取的范围分别在其左右子树上，于是可以再进行一次迭代：

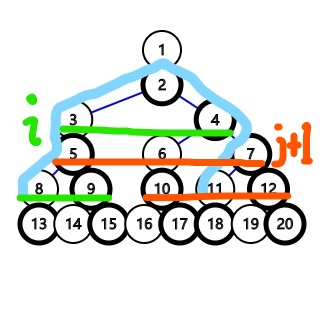
可以看出，其左右能取的白色节点个数将变成第\(i\)行及第\(j+1\)行的白色节点个数

于是可以写出式子\(f[i+j]+=sumb[n-max(i,j)]*w[i]*w[j+1]\)

而对\(w[]\)、\(sumw[]\)及\(sumb[]\)可以用斐波那契树的斐波那契数列性质求出

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
const int P=123456789;
typedef long long ll;
ll n;
ll w[N],b[N],sumw[N],sumb[N],f[N];
int main(){
	scanf("%lld",&n);
	sumw[1]=sumw[2]=sumb[2]=w[1]=b[2]=1,sumb[1]=w[2]=b[1]=0;
	for(ll i=3;i<=n;i++){
		w[i]=(w[i-1]+w[i-2])%P;
		b[i]=(b[i-1]+b[i-2])%P;
		sumw[i]=(sumw[i-1]+w[i])%P;
		sumb[i]=(sumb[i-1]+b[i])%P;
	}
	for(ll i=1;i<=n;i++)f[i]=(sumw[n-i]*w[i+1])%P;
	for(ll i=1;i<=n;i++)for(ll j=1;j<=n;j++)f[i+j]=(f[i+j]+sumb[n-max(i,j)]*w[i+1]%P*w[j]%P)%P;
	for(ll i=1;i<=n*2;i++)printf("%lld ",f[i]);
}