\(Description:\)
\(Iahub\)非常喜欢树木。最近,他发现了一棵有趣的树,名为传播树。
该树由从\(1\)到\(N\)编号的\(N\)个节点组成,每个节点\(i\)都有一个初始值\(a_i\)。树的根节点为\(1\)。
该树具有一个特殊的属性:节点$$i的值增加\(val\)时,\(i\)的所有子节点将会减少\(val\)。请注意,此时\(i\)的所有子节点的子节点还将增加\(val\),以此类推。
本题有 \(M\)个询问,分为两种:
"\(1\) \(x\) \(val\)" 将节点\(x\)的值增加\(val\)
"\(2\) \(x\)" 查询节点\(x\)的当前值
\(Input\) \(Format:\)
第一行包含两个整数\(N,M\)如题目描述所说
第二行包含\(N\)个整数,\(a_1\),\(a_2\),...,\(a_n\)
接下来\(N−1\)行有两个整数\(u,v\),代表两者之间存在一条边
接下来的m行中的每行都包含上述格式的查询
\(Output\) \(Format:\)
对于每个类型为\(2\)的查询(查询节点$$x的值),按照输入中给出的顺序在单独的行上回答查询
\(Sample\) \(Input:\)
5 5
1 2 1 1 2
1 2
1 3
2 4
2 5
1 2 3
1 1 2
2 1
2 2
2 4
\(Sample\) \(Output:\)
3
3
0
\(Hint:\)
- \(1 \leq n,m \leq 200,000\)
- \(1\leq a_i,val \leq 1000\)
- \(1 \leq v_i,u_i,x \leq n\)
\(Solution:\)
考虑到传播树棵树一个点修改后其子树每隔两行的差值不变,我们可以将整个树变成两棵树,分别以\(1\)号与\(0\)号节点为子树,隔两行建树
如下图
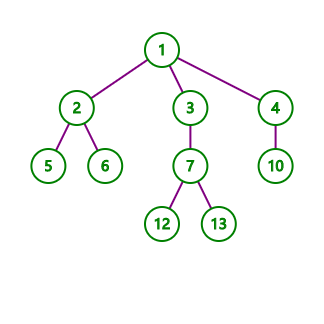
可将其分成这两个树:
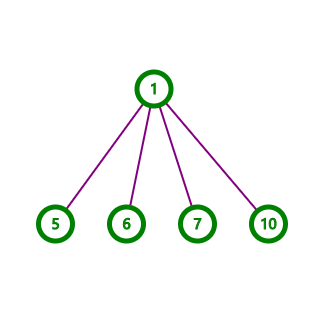
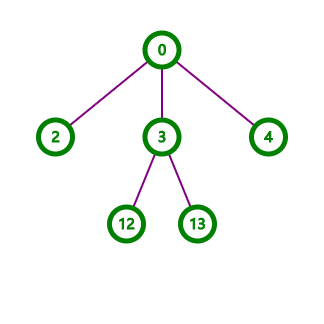
而直接树上查分也会\(TLE\),只能以树状数组更新、查询。
于是可以先遍历一遍原来的边建出新边,并处理出每个点所在的新树及两个树的大小及每个点在原树的父亲节点。
再分别对两棵新建的树遍历,处理出两棵树各自每个点的\(DFS\)序的出入时间戳,记为\(l[\) \(]\)与\(r[\) \(]\) 。
由于更新\(x\)节点时不仅要将\(x\)所在的新树的\(x\)的子树加上\(v\),还要将原来树下一行所在的新树减去\(v\),故需处理出每个点下一行所在子树的最小\(l\)值与最大\(r\)值,存为\(minl[\) \(]\)与\(maxr[\) \(]\),这可以在遍历新树时不断更新其原树的父节点。
而对初始的值可以先不管,在输出时加上即可。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=500050;
int n,m,x,y,ii,t,p,k,w;
int to[N],to1[N];
int nextn[N],nextn1[N];
int h[N],h1[N];//后带1的为新边
int l[3][N];//新树的时间戳进该点的值
int r[3][N];//新树的时间戳出该点的值
int a[N];//各点的初始值
int bn[2];//两个树的大小
int f[3][N];//两个树的树状数组
int anc[N];//原树的父节点
int minl[N];//原树的儿子节点最小的l值
int maxr[N];//原树的儿子节点最大的r值
bool b[N];//记录该点在哪棵树
void dfs(int x,int ancs,int foreanc){//ancs为x父节点,foreanc为x的父节点的父节点
if(foreanc!=-1){
ii++;
to1[ii<<1|1]=foreanc;
nextn1[ii<<1|1]=h1[x];
h1[x]=ii<<1|1;
to1[ii<<1]=x;
nextn1[ii<<1]=h1[foreanc];
h1[foreanc]=ii<<1;//建新边
b[x]=b[foreanc];
}
anc[x]=ancs;
bn[b[x]]++;
for(int i=h[x];i;i=nextn[i]){
y=to[i];
if(y==ancs)continue;
dfs(y,x,ancs);
}
}
void dfs1(int x,int ancs){
t++;
l[b[x]][x]=t;
minl[anc[x]]=min(minl[anc[x]],l[b[x]][x]);
for(int i=h1[x];i;i=nextn1[i]){
y=to1[i];
if(y==ancs)continue;
dfs1(y,x);
}
r[b[x]][x]=t;
maxr[anc[x]]=max(maxr[anc[x]],r[b[x]][x]);
}
inline int lowbit(int x){
return x&(-x);
}
void update(int x,int w,bool b){
for(int i=x;i<=bn[b]&&i;i+=lowbit(i))f[b][i]+=w;
}
int getsum(int x,bool b){
int cnt=0;
for(int i=x;i;i-=lowbit(i))cnt+=f[b][i];
return cnt;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
to[i<<1|1]=y;
nextn[i<<1|1]=h[x];
h[x]=i<<1|1;
to[i<<1]=x;
nextn[i<<1]=h[y];
h[y]=i<<1;
minl[x]=0x6ffffff;
}
minl[n]=0x6ffffff;
b[1]=1;
bn[0]++;
dfs(1,0,-1);
dfs1(1,0);
t=0;
dfs1(0,-1);
while(m--){
scanf("%d",&p);
if(p==1){
scanf("%d%d",&k,&w);
update(l[b[k]][k],w,b[k]);
update(r[b[k]][k]+1,-w,b[k]);
if(minl[k]!=0x6ffffff)update(minl[k],-w,b[k]^1);
if(maxr[k])update(maxr[k]+1,w,b[k]^1);
}
if(p==2){
scanf("%d",&k);
int cnt=0;
cnt+=getsum(l[b[k]][k],b[k]);
printf("%d\n",cnt+a[k]);
}
}
}





