\(Description\):
\(Yixght\)是名为\(SzqNetwork(SN)\)的公司经理。 现在,她非常担心,因为她刚刚收到一个坏消息,这表明\(SN\)的业务竞争对手\(DxtNetwork(DN)\)打算攻击SN的网络。 更不幸的是,\(SN\)的原始网络非常薄弱,我们只能将其视为一棵树。 形式上,SN网络中有 \(N\) 个节点, \(N−1\)个双向通道连接这些节点,并且始终存在从任何节点到另一个节点的路由路径。 为了保护网络免受攻击,\(Yixght\)在某些节点之间建立了 \(M\)个新的双向通道。
作为\(DN\)的最佳黑客,您可以准确地破坏两个通道,一个破坏原始网络,另一个破坏M个新渠道。 现在,您的上司想知道您可以采用多少种方式将SN网络划分为至少两个部分。
\(Input Format\):
输入文件的第一行包含两个整数:$ N,M $ 。 代表节点数和新通道数。
\(N−1\)行表示SN原始网络中的信道,每对 \(a,b\)表示在节点 \(a\) 和节点 \(b\) 之间已经存在一个信道。
接下来的 \(M\) 行代表网络中的新添加信道,每对 \(a,b\) 表示节点 \(a\) 和节点 \(b\) 之间会添加一个新信道。
\(Output Format\):
输出一个整数。将网络划分为至少两个部分的方式的数量。
\(Sample Input\):
4 1
1 2
2 3
1 4
3 4
\(Sample Output\):
3
\(Hint\):
- 20%的数据 \(1 \leq N,M \leq 10\)
- 40%的数据 \(1 \leq N,M \leq 1000\)
- 100%的数据 \(1 \leq N,M \leq 100,000\)
\(Solution\):
很容易想到树上边差分
对每条新加入的边\((x,y)\),差分数组\(s\)便\(s[x]++,s[y]++,s[lca(x,y)]-=2\),最后\(dfs\)一遍统计出每个点有多少条新加的边经过,用\(d\)数组维护。
若\(d[i]=0\) 则删去这一条边与新加的任意一条边皆可将\(i\)这个点及其子树分离出来,\(ans+=M\)。
若\(d[i]=1\) 则这个点与一条新边相连,删去原来的边与这条新边也能将\(i\)与其子树分出,\(ans++\)。
若\(d[i] \geq 2\) 则这个点与\(\geq 3\)条边相连,无论怎么删都不行。
还有一点,根节点\(1\)在最后总会是0,但\(ans\)不能直接加\(M\),因为若\(1\)与其他节点相连则会多加,还需特判一下。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=500000;
typedef long long ll;
ll n,m,x,y,ans,f1,f2;
ll to[N];
ll nextn[N];
ll h[N];
ll deg[N];
ll f[N][20];
ll s[N];
ll d[N];
bool b[N];
void dfs(ll x,ll anc,ll dep){
b[x]=1;
f[x][0]=anc;
deg[x]=dep;
for(ll i=1;i<20;i++)f[x][i]=f[f[x][i-1]][i-1];
for(ll i=h[x];i;i=nextn[i]){
ll y=to[i];
if(b[y])continue;
if(x==1)f1++;
dfs(y,x,dep+1);
}
}
ll lca(ll x,ll y){
if(deg[x]>deg[y])swap(x,y);
for(ll i=19;i>=0;i--)if(deg[f[y][i]]>=deg[x])y=f[y][i];
if(x==y)return x;
for(ll i=19;i>=0;i--)if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
return f[x][0];
}
ll dfs1(int x,int anc){
d[x]=s[x];
for(int i=h[x];i;i=nextn[i]){
int y=to[i];
if(y==anc)continue;
d[x]+=dfs1(y,x);
}
return d[x];
}
int main(){
scanf("%d%d",&n,&m);
for(ll i=1;i<n;i++){
scanf("%d%d",&x,&y);
to[2*i-1]=y;
nextn[2*i-1]=h[x];
h[x]=2*i-1;
to[2*i]=x;
nextn[2*i]=h[y];
h[y]=2*i;
}
dfs(1,1,1);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
s[x]++;
s[y]++;
s[lca(x,y)]-=2;
if(x==1||y==1)f2++;
}
dfs1(1,0);
for(ll i=2;i<=n;i++){
if(!d[i])ans+=m;
if(d[i]==1)ans++;
}
if(f1+f2==1)ans+=m;
if(f1==1&&f2==1)ans++;
printf("%lld",ans);
}
然而,还有一个优化: 打错lca还能过时想到的
对于每新加入的边\((x,y)\),\(s\)数组仅\(s[x]++,s[y]++\)
在最后统计出的\(d\)数组便可与之前一样算\(ans\)且少了根结点的特判。
比如这张图:
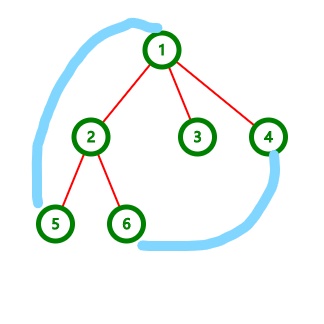
(蓝色边为新加边)
原先的\(s\)与\(d\)数组的值如下:
| 数组 |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
| \(s\) |
\(-3\) |
\(0\) |
\(0\) |
\(1\) |
\(1\) |
\(1\) |
| \(d\) |
\(0\) |
\(2\) |
\(0\) |
\(1\) |
\(1\) |
\(1\) |
那按这种方法的\(s\)与\(d\)数组的值如下:
| 数组 |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
| \(s\) |
\(1\) |
\(0\) |
\(0\) |
\(1\) |
\(1\) |
\(1\) |
| \(d\) |
\(3\) |
\(2\) |
\(0\) |
\(1\) |
\(1\) |
\(1\) |
可以看出,除\(1\)节点外,新的\(d\)数组的\(0\)的个数与\(1\)的个数似乎与之前一样
确实,只要是 子树与该点 没有在新边上的 叶子节点的\(d\)值都将是0,\(ans\)照样\(+M\)。
而\(d[i]=1\)则蕴涵\(s[i]=1\),所以\(i\)与新增一边相邻,与之前一样,\(ans++\)。
对于\(1\)节点,无论如何都不会是\(0\)或\(1\),除非\(M=0\),这种情况直接排除。
于是代码如下,相对快很多:
#include<bits/stdc++.h>
using namespace std;
const int N=500000;
typedef long long ll;
ll n,m,x,y,ans,xx,yy,ii,jj;
ll to[N];
ll nextn[N];
ll h[N];
ll s[N];
ll d[N];
ll dfs(int x,int anc){
d[x]=s[x];
for(int i=h[x];i;i=nextn[i]){
int y=to[i];
if(y==anc)continue;
d[x]+=dfs(y,x);
}
return d[x];
}
int main(){
scanf("%d%d",&n,&m);
for(ll i=1;i<n;i++){
scanf("%d%d",&x,&y);
to[2*i-1]=y;
nextn[2*i-1]=h[x];
h[x]=2*i-1;
to[2*i]=x;
nextn[2*i]=h[y];
h[y]=2*i;
}
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
s[x]++;
s[y]++;
}
dfs(1,0);
for(ll i=1;i<=n;i++){
if(!d[i])ans+=m;
if(d[i]==1)ans++;
}
printf("%lld",ans);
}






