树上的链

Description

　给定一棵 \(n\) 个点的树和树上的 \(m\) 条链，请问有多少对链有至少一个公共点。

Input

第一行两个正整数 \(n,m\)。 第 \(2\)~\(n\) 行，每行两个整数 \(s,t\)，表示有一条边连接 \(s\) 点和 \(t\) 点。

接下来 \(m\) 行，每行两个整数 \(a,b\)，表示有一条链的起点、终点分别为 \(a,b\)。（链的起点、 终点可能相同）

Output

*一行一个整数，表示答案。

Sample Input

5 3
1 2
1 3
2 4
2 5
4 5
1 4
3 5

Sample Output

3

hint

• 对于 30%的数据，\(n,m \leq 100\)

• 对于 50%的数据，\(n,m \leq 2000\)

• 对于另 20%的数据，读入的 \(s,t\) 满足 \(t=s+1\)

• 对于100%的数据，\(1 \leq n,m \leq 100000\)

• 时间限制：\(1s\) 空间限制：\(512MB\)

solution

为方便起见，以下提到的一条链的\(LCA\)指这条链两个端点的\(LCA\)，一条链的\(LCA\)必为这条链最高的点），树上两条链相交，只有两种情况：

• 一条链的\(LCA\)交另一条链的\(LCA\)：

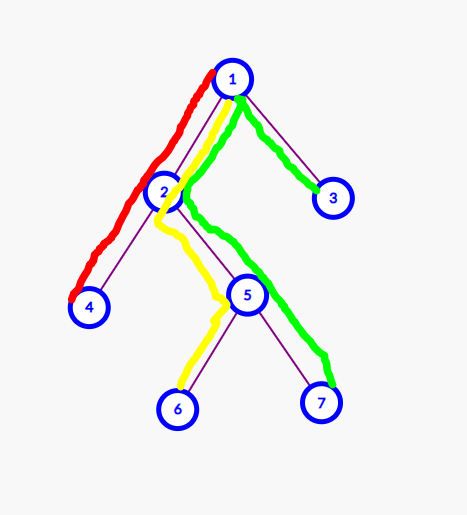（图\(1\)）

　* 一条链交另一条链几条边：

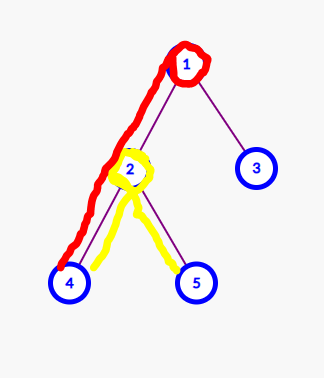（图\(2\)）

对于第一种情况，仅有的可能就是两条链相交于各自链的\(LCA\)，也即两条链的\(LCA\)相同。于是我们可以设置一个数组 \(k\) 维护一个点是多少条链的 \(LCA\)，最后遍历时 将 \(ans\) 加上每个点 \(x\) 对应是多少条链的 \(LCA\) 的数量中 选出两个，组成一对，即 $\frac {k [ x ] \times ( k [ x ] - 1 )}{2} $ 即可。

对于第二种情况，可以先预处理出每个节点 \(x\) 到根节点上共经过几条链，用数组 \(l\) 维护。\(l\) 怎么求？显然有 \(l [ x ] = l [ anc [ x ] ] + k [ x ]\) （\(k\)即每个点是多少条链的\(LCA\)，\(anc [ x ]\) 是\(x\)的父亲节点）

那么一条链一共出现这种情况的个数为 \(l [ x ] + l [ y ] - 2 \times l [ lca( x , y ) ]\)（\(x\) 与$ y$ 为一条链的起始点与终点）。

两种情况会不会重复呢？

假设有一条链\(a\)的\(LCA\)与另一条链\(b\)的\(LCA\)重合，那链\(a\)的首、尾、顶节点的$ l$ 值都包含链\(b\)所贡献的 \(1\)，在最后计算的时候贡献的只剩\(1+1-2\times 1=0\)，没有重复。（图\(1\)中三条链虽然有边相交仍属第\(1\)种情况，没多算）

是否会在第二种情况中，两条链都算了另一条一次，不除以\(2\)呢？

由于$l [ x ] = l [ anc [ x ] ] + k [ x ] $ ，若 \(a\) 链的\(LCA\)离顶点的距离大于 \(b\) 链的\(LCA\)离顶点的距离，那在算 \(a\) 链时将不会记录 \(b\) 链的贡献，只会在算 \(b\) 链时算上 \(a\) 链的贡献，依然只算了一次。（图\(2\)中红黄两链仅在算红链时算入黄链的贡献）

上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=500050;
typedef long long ll;
ll n,m,ans,x,y;
ll to[N];
ll nextn[N];
ll h[N];
ll deg[N];//深度
ll anc[N];
ll f[N][20];
ll k[N];//一点是多少条链的LCA
ll l[N];//一点到根节点共有多少条链
ll st[N];//记录链的起点
ll en[N];//记录链的终点
ll lc[N];//记录链的LCA
void dfs(int x,int ancs,int dep){
	f[x][0]=ancs;
	anc[x]=ancs;
	deg[x]=dep;
	for(int i=1;i<20;i++)f[x][i]=f[f[x][i-1]][i-1];
	for(int i=h[x];i;i=nextn[i]){
		int y=to[i];
		if(y==ancs)continue;
		dfs(y,x,dep+1);
	}
}//预处理
int lca(int x,int y){
	if(deg[x]>deg[y])swap(x,y);
	for(int i=19;i>=0;i--)if(deg[f[y][i]]>=deg[x])y=f[y][i];
	if(x==y)return x;
	for(int i=19;i>=0;i--)if(f[x][i]!=f[y][i]){
		x=f[x][i];
		y=f[y][i];
	}
	return f[x][0];
}//求LCA
void dfs1(int x,int ancs){
	l[x]=l[ancs]+k[x];
	ans+=k[x]*(k[x]-1)/2;//第一种情况
	for(int i=h[x];i;i=nextn[i]){
		int y=to[i];
		if(y==ancs)continue;
		dfs1(y,x);
	}
}
int main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<n;i++){
		scanf("%d%d",&x,&y);
		to[i<<1|1]=y;
		nextn[i<<1|1]=h[x];
		h[x]=i<<1|1;
		to[i<<1]=x;
		nextn[i<<1]=h[y];
		h[y]=i<<1;
	}//建树
	dfs(1,0,1);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&st[i],&en[i]);
		lc[i]=lca(st[i],en[i]);
		k[lc[i]]++;
	}
	dfs1(1,0);
	for(int i=1;i<=m;i++)ans+=l[st[i]]+l[en[i]]-2*l[lc[i]];//第二种情况
	printf("%lld",ans);
}