湖南省队集训2021题解
不知道写什么题于是补一下去年的集训题
部分题没补,都是题目涉及的算法我还没学过
Day1
T1 数列
设 \(f_i\) 表示以 \(i\) 结尾的最大值,设 \(l_i,r_i\) 表示 \(a_i\) 覆盖到的左右端点 考虑写出一个比较显然的式子:
这时候就能直接二维偏序套李超树,\(O(n\log_2^2 n)\) 无法通过此题。
但是可以发现去掉二维偏序的约束直接转移是对的。也就是说不满足约束条件的决策无法更新最大值
具体的,设 \(k\) 为 \([i,j]\) 内最大值的位置,只考虑 \(a_k > \max(a_i,a_j)\) 的情况,那么 $$(a_i-a_j)^2 < (a_k-a_i)^2 + (a_k - a_j)^2$$
所以 \(j\) 这个决策显然不优于 \(k\)。
于是我们直接李超线段树斜率优化即可。时间复杂度 \(O(n\log_2n)\)
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e6+5;
int n,C,ans,t[N<<2],k[N],b[N],a[N];
int w(int p,int x){return k[p]*x+b[p];}
void update(int p,int l,int r,int x){
int vl=w(x,l),vr=w(x,r);
int cl=w(t[p],l),cr=w(t[p],r);
if(!t[p]||(vl>=cl&&vr>=cr))return t[p]=x,void();
if(vl<=cl&&vr<=cr)return;
int mid=l+r>>1;
update(p<<1,l,mid,x);update(p<<1|1,mid+1,r,x);
}
int query(int p,int l,int r,int x){
if(l==r)return w(t[p],x);
int mid=l+r>>1;int ret=w(t[p],x);
if(x<=mid)ret=max(ret,query(p<<1,l,mid,x));
else ret=max(ret,query(p<<1|1,mid+1,r,x));
return ret;
}
signed main(){
freopen("array.in","r",stdin);
freopen("array.out","w",stdout);
scanf("%lld%lld",&n,&C);
int ret=0;int mx=0;
k[0]=-1e9;
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
mx=max(mx,a[i]);
}
for(int i=1,x;i<=n;i++){
x=a[i];
if(i==1)ans=0;
else ans=query(1,1,mx,x)+C+x*x;
k[i]=-2*x;b[i]=x*x+ans;
update(1,1,mx,i);
ret=max(ret,ans);
}
return printf("%lld\n",ret),0;
}
T2 差量
先通过一次 \(M2\) 求得全局的极差,然后二分一个前缀的极差是否等于全局的极差。
此时我们可以确定最大值最小值其中一个的位置 。再随意询问一个位置的值即可知道是最小还是最大,,并且设最后得到的这个位置为 \(x\)。
考虑使用二进制分组,设 \(S_i\) 表示二进制下下标的第 \(i\) 位为 \(1\) 的所有下标集合。
分别查询 \(S_i\) 和 \(S_i \cup x\) 再去重可以知道 \(S_i\) 所有数的值。
设 $ cnt_i $ 表示 \(i\) 二进制下 \(1\) 的个数,那么 \(a_i\) 必定在所有的 \(S_i\) 恰好出现了 \(cnt_i\) 次,并且有且仅有一个数满足这个条件。
最后统计一下 \(M2\) 操作的使用次数 : 二分 \(\log_2n\) , 查询 \(S_i\) 和 \(S_i \cup x\) 也是 \(\log_2n\),所以总共是 \(3\log_2n\)
Code
#include "difference.h"
#include<bits/stdc++.h>
// using namespace std;
// const int sid = 300 + 5;
// static int n, T1, T2, M1, M2;
// static int a[sid];
// static void error(const char *msg) {
// printf("%s\n", msg);
// exit(0);
// }
// static void init() {
// T1 = T2 = 0;
// scanf("%d%d%d", &n, &M1, &M2);
// for(int i = 0; i < n; i ++) scanf("%d", &a[i]);
// srand(time(0) | n ^ (M2 * M1));
// }
// int qry1(int i) {
// if(++ T1 > M1) error("too many 1 operators !");
// if(i < 0 || i >= n) error("the argument i in 1 operator is not in [0, n - 1]");
// return a[i];
// }
// static vector<int> to_see, ans ;
// int abs(int x) { return (x > 0) ? x : -x; }
// vector<int> qry2(const vector<int> &S) {
// if(++ T2 > M2) error("too many 2 operators !");
// to_see = S; sort(to_see.begin(), to_see.end());
// for(int i = 0; i < to_see.size(); i ++) {
// if(to_see[i] < 0 || to_see[i] >= n) error("the argument i in 2 operator is not in [0, n - 1]");
// if(i && to_see[i] == to_see[i - 1]) error("the argument i in 2 operator are not unique");
// }
// ans.clear();
// for(int i = 0; i < to_see.size(); i ++) for(int j = 0; j < i; j ++)
// ans.push_back( abs( a[ to_see[i] ] - a[ to_see[j] ] ) );
// random_shuffle(ans.begin(), ans.end());
// return ans ;
// }
// void answer(const vector<int> &ret) {
// if(ret.size() != n) error("your answer's length is not n");
// for(int i = 0; i < ret.size(); i ++)
// if(ret[i] != a[i]) error("Wrong Answer");
// printf("Correct!\n");
// printf("You use (%d) operator 1 and (%d) operator 2\n", T1, T2);
// exit(0);
// }
// void find(int n,int M1,int M2);
using namespace std;
const int N=255;
vector<int>Q,S,S0,S1;
multiset<int>s[11];
int Ans[N],lg[N];
map<int,int>mp;
int get(int x){
Q.clear();S.clear();
for(int i=0;i<=x;i++)Q.push_back(i);
S=qry2(Q);
sort(S.begin(),S.end());
return *(--S.end());
}
int calc(int x){int S=0;for(;x;x>>=1)if(x&1)S++;return S;}
vector<int>ret;
void find(int n,int M1,int M2){
int l=0,r=n-1,mx=get(n-1);
while(l<=r){
int mid=l+r>>1;
if(get(mid)==mx)r=mid-1;
else l=mid+1;
}
Ans[l]=qry1(l);Ans[0]=qry1(0);
int sign=Ans[l]<Ans[0]?1:-1;
for(int i=2;i<=n-1;i++)lg[i]=lg[i>>1]+1;
for(int i=0;i<=lg[n-1];i++){
S.clear();S0.clear();S1.clear();s[i].clear();
for(int j=0;j<n;j++)
if(((j>>i)&1)&&j!=l)S.push_back(j);
S0=qry2(S);S.push_back(l);S1=qry2(S);
for(auto v:S1)s[i].insert(Ans[l]+sign*v);
for(auto v:S0)s[i].erase(s[i].find(Ans[l]+sign*v));
}
for(int i=1;i<n;i++){
if(i==l)continue;
mp.clear();
for(int j=0;j<=lg[n-1];j++)
if((i>>j)&1)for(auto v:s[j])mp[v]++;
else for(auto v:s[j])mp[v]-=300;
int now=calc(i);
int fk=0;
for(auto v:mp)if(v.second==now){Ans[i]=v.first;fk++;}
}
for(int i=0;i<n;i++)ret.push_back(Ans[i]);
answer(ret);
}
// int main() {
// //freopen("difference20.in","r",stdin);
// //int id;scanf("%d",&id);
// init();
// find(n, M1, M2);
// return 0;
// }
T3 异或
std 写了 9k 的 容斥+FWT 逆天神题,不会
极限得分 : 25 pts
Day2
T1 NOI!
应该是省集里最水的一道题了。。。
如果 \((x,y)\) 要染色那么 \((x+5,y+5)\) 一定也会被染色。
考虑按 \((x\bmod 5,y\bmod 5)\) 分类,然后做 \(25\) 遍扫描线即可。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int n;
struct{
int len[(N/5)*4],cnt[(N/5)*4];
struct Node{
int l,r,x;
Node(){}
Node(int L,int R,int X){l=L;r=R;x=X;}
};
vector<Node>q[N/5];
void ins(int X1,int Y1,int X2,int Y2){
q[X1].push_back(Node(Y1,Y2,1));
q[X2+1].push_back(Node(Y1,Y2,-1));
}
void update(int p,int l,int r){
if(l==r)len[p]=cnt[p]?1:0;
else if(cnt[p]==0)len[p]=len[p<<1]+len[p<<1|1];
else len[p]=r-l+1;
}
void change(int p,int l,int r,int x,int y,int v){
if(x<=l&&y>=r){
cnt[p]+=v;
update(p,l,r);
return;
}
int mid=l+r>>1;
if(x<=mid)change(p<<1,l,mid,x,y,v);
if(y>mid)change(p<<1|1,mid+1,r,x,y,v);
update(p,l,r);
}
int work(){
int ans=0;
for(int i=0;i<=n/5+1;i++){
for(auto v:q[i])change(1,0,n/5+1,v.l,v.r,v.x);
ans+=len[1];
}return ans;
}
}T[5][5];
signed main(){
freopen("q.in","r",stdin);
freopen("q.out","w",stdout);
int Q;scanf("%lld%lld",&n,&Q);
while(Q--){
int X1,Y1,X2,Y2;
scanf("%lld%lld%lld%lld",&X1,&Y1,&X2,&Y2);
X1--;Y1--;X2--;Y2--;
for(int i=0;i<5;i++)
for(int j=0;j<5;j++){
int xx1,yy1,xx2,yy2;
if(i<X1%5)xx1=X1/5+1;
else xx1=X1/5;
if(j<Y1%5)yy1=Y1/5+1;
else yy1=Y1/5;
if(i>X2%5)xx2=X2/5-1;
else xx2=X2/5;
if(j>Y2%5)yy2=Y2/5-1;
else yy2=Y2/5;
int nx=xx1*5+i,ny=yy1*5+j;
if(!(nx>=X1&&ny>=Y1&&nx<=X2&&ny<=Y2)||xx1<0||yy1<0||xx2<0||yy2<0)continue;
if(((ny-Y1)*(X2-X1+1)+(nx-X1))%5==0)T[i][j].ins(xx1,yy1,xx2,yy2);
}
}
int ans=0;
for(int i=0;i<5;i++)
for(int j=0;j<5;j++)ans+=T[i][j].work();
printf("%lld\n",ans);
return 0;
}//6 10 19 78
T2 模拟?
首先删边最大独立集最多 \(+1\),加边最大独立集不变大
考虑删边 \(u,v\) : 想一想满足什么条件下会 \(+1\) ,那么就是当断开\(u,v\)后,选 \(u,v\) 比不选 \(u,v\) 各大 \(1\)。
考虑加边 \(x,y\) : 如果 \(x,y\) 分别是 \(u,v\) 最大独立集中的必选点 ,那么答案就会 \(-1\)。
考虑暴力枚举删哪条边,然后树形 \(dp\) 两棵树,求出必选点的个数即可。
事实上必选点可以直接通过儿子节点的必选点个数推出。设 \(cnt_i\) 表示 \(i\) 节点儿子的必选点的个数。
那么 必选\可选可不选\必不选 分别对应 \(cnt_i = 0\) , \(cnt_i = 1\) , \(cnt_i > 1\)。
写出这个 \(O(n^2)\) 暴力后我们发现是可以直接换根 \(dp\) 的。所以换根和自底向上推写起来是差不多的。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,g[N][3],f[N][3],h[N][3];
int op0[N],op1[N],siz[N];
vector<int>G[N];
void dfs0(int u,int F){
siz[u]=1;g[u][2]=1;
int cnt=0;
for(auto v:G[u]){
if(v==F)continue;
dfs0(v,u);cnt+=op0[v]==2;
siz[u]+=siz[v];
for(int i=0;i<=2;i++){
int j=op0[v];
if(i==2&&j==1)j=0;
if(i==1&&j==2)j=1;
g[u][i]+=g[v][j];
}
}
if(cnt>1)op0[u]=0;
else if(cnt==1)op0[u]=1;
else op0[u]=2;
}
void dfs1(int u,int F){
memcpy(h[u],g[u],sizeof(h[u]));
for(int i=0;i<=2;i++){
int j=op1[u];
if(i==2&&j==1)j=0;
if(i==1&&j==2)j=1;
h[u][i]+=f[u][j];
}
int cnt=(op1[u]==2);
for(auto v:G[u])if(v!=F)cnt+=(op0[v]==2);
for(auto v:G[u]){
if(v==F)continue;
cnt-=(op0[v]==2);
if(cnt>1)op1[v]=0;
else if(cnt==1)op1[v]=1;
else op1[v]=2;
cnt+=(op0[v]==2);
for(int i=0;i<=2;i++){
int j=op0[v];
if(i==2&&j==1)j=0;
if(i==1&&j==2)j=1;
f[v][i]=h[u][i]-g[v][j];
}
}
for(auto v:G[u])if(v!=F)dfs1(v,u);
}
int main(){
freopen("i.in","r",stdin);
freopen("i.out","w",stdout);
scanf("%d",&n);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
G[u].push_back(v);G[v].push_back(u);
}
dfs0(1,0);dfs1(1,0);
long long ans=0;
for(int i=2;i<=n;i++){
if(op0[i]!=2||op1[i]!=2)continue;
ans+=(n-siz[i])*1LL*siz[i]-g[i][2]*1LL*f[i][2];
}
printf("%lld\n",ans);
return 0;
}
T3 AK啦!
逆天智商题。
如果查询 \((x,y)\) 为 \(0\) 的话,那么查两次可以确定是竖线还是横线。
如果查询 \((x,y)\) 为 \(k\) 的话,那么 \((x+k,y+k) , (x-k,y-k)\) 必有一个是 \(0\)。
考虑只在 \(x=y\) 这条线上询问。那么就变成了一维问题。考虑分治实现。
每次询问 \(mid = (l+r)/2\) 得到 \(d\) , 递归 \([l,mid-d]\) 和 \([mid+d,r]\) 继续做。
Code
#include<bits/stdc++.h>
#include "grader.cpp"
#define vc vector<int>
#define pvv pair<vc,vc>
using namespace std;
const int INF=1e8;
vector<int>X,Y,ans;
int pos;
void solve(int l,int r){
if(l>r)return;
int mid=(l+r)/2;
int d=query(mid,mid);
if(!d)ans.push_back(mid),d=1;
else pos=mid;
solve(l,mid-d);solve(mid+d,r);
}
pvv solve(){
solve(-INF,INF);
for(auto v:ans){
if(!query(pos,v))X.push_back(v);
if(!query(v,pos))Y.push_back(v);
}
return pvv(X,Y);
}
Day 3
T1 合成小丹
把 $ \lfloor \frac{x}{2} \rfloor$ 看成二进制的右移 \(1\) 位。所以 $ \lfloor \frac{x}{2} \rfloor$ \(|\) $ \lfloor \frac{y}{2} \rfloor = $ $ \lfloor \frac{x|y}{2} \rfloor$ 。
设 \(d_i\) 为 \(a_i\) 参与合并的次数,在仅考虑合并操作的情况下,
那么答案就是所有 \(\lfloor \frac{a_i}{2^{d_i}} \rfloor\) 或起来,一组 \(d_i\) 合法当且仅当 \(\sum \frac{1}{2^{d_i}} = 1\)。
加上删除操作后就是 \(\sum \frac{1}{2^{d_i}} \ge 1\)。
我们设 $S= { 1,2,3...n } $ , 那么当 \(\sum \frac{1}{2^{d_i}} \ge 1\) 是否一定存在一个 \(\sum_{i \in S}\frac{1}{2^{d_i}} = 1\) 呢?答案是肯定的。这个随手证一下就好了
此时我们确定了一个思路: 在满足条件的情况下 \(\sum \frac{1}{2^{d_i}}\) 越大越好,我们考虑从高到低位贪心填数。然后用上面的结论计算出当前的 \(d_i\) 再判断 \(\sum \frac{1}{2^{d_i}} \ge 1\) 即可。
这个算法复杂度是 \(O(Tnw^2)\) 的,理论上过不了,但赛时有人实现精细是过了的。
我们考虑用位运算的性质优化掉一个 \(w\) 。
对于每个 \(a_i\) 设一个 \(b_i\) , \(b_i\) 的第 \(j\) 位为 \(1\) 表示 \(a_i\) 右移 \(j\) 位和答案或起来不等于答案本身。
那么 \(b_i\) 的最低位 \(0\) 就是 \(d_i\) 的最优取值。所以只要维护当答案某一位由 \(1\) 变 \(0\) 时 \(b_i\) 的变化即可。
设变化的的位置为第 \(t\) 位,不难发现此时只要使 \(b_i = b_i | (a_i >> t)\) 即可。
最后提及一个小 \(trick\) , 如果知道 \(2^k\) 次方 想 \(O(1)\) 求出 \(k\) 是多少,可以运用费马小定理。
(偷懒写了 \(O(Tnw^2)\) )
Code
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int n,w;
ll a[N];
inline int rdi(){
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
return x;
}
inline ll rdl(){
ll x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
return x;
}
int lg[N];
inline bool check(ll x,int pos){
ll ret=0;int tt=0;
for(int i=1;i<=n;i++){
tt=w;
for(int j=0;j<w;j++){
if(((a[i]>>j)|x)^x)tt--;
else break;
}
ret+=(1LL<<tt);
if(ret>=(1LL<<w))return 1;
}
return 0;
}
signed main(){
freopen("merge.in","r",stdin);
freopen("merge.out","w",stdout);
int Q;scanf("%d",&Q);
srand(time(0));srand(rand());
while(Q--){
n=rdi();w=rdi();
ll ans=0;
for(int i=1;i<=n;i++){
a[i]=rdl();
//lg[i]=log2(a[i]);
//out(a[i]);
}sort(a+1,a+n+1);
for(int i=w-1;i>=0;i--){
ll now=(ans<<1);
for(int j=i-1;j>=0;j--)now=(now<<1|1);
if(check(now,i-1))ans=(ans<<1);
else ans=(ans<<1|1);
}
printf("%lld\n",ans);
}
return 0;
}
T2 路过中丹
考虑有解的条件。我们发现如果 \([l,r]\) 存在长度为 \(3\) 的回文串那么一定可行。
例如 \(abxyxcd\),\(xyxbabxyxcdcxyxcdcxyxbabxyx\) 即可。
如果不存在显然就是判断 \([l,r]\) 是否存在偶回文串覆盖。
我们设 \(l_i,r_i\) 分别为以 \(i\) 开始和以 \(i\) 结束的最短偶回文串。
那么就是判断 \(L,R\) 中是否存在 \(l_i < L\) 且 \(r_i > R\)。
这个东西拿 manacher + 单调栈 可以轻松搞。
搞出来后可以离线询问,双指针 + 线段树 维护即可。
但是我们有更暴力的做法:
枚举到每个 \(i\) 的时候往前暴力求出以 \(i\) 结尾的最短偶回文串的开始位置 \(j\)。
接着对 \([i,j]\) 这段区间搞个区间取 \(max\) ,在随机情况下是很快的。
标算写的是 分治 + PAM上倍增。不会。
Code
#include<bits/stdc++.h>
#define ull unsigned long long
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5;
const ull B=163;
int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=10*x+ch-'0',ch=getchar();
return x;
}
int n,q;
char s[N];bool ans[N];
ull pw[N],s0[N],s1[N];
vector<pii>qr[N];
int C[N];
void add(int x){for(;x<=n;x+=x&-x)C[x]++;}
int ask(int x){int S=0;for(;x;x-=x&-x)S+=C[x];return S;}
int tag[N<<2],mn[N<<2];
void update(int p){mn[p]=min(mn[p<<1],mn[p<<1|1]);}
void pushdown(int p){
if(!tag[p])return;
mn[p<<1]=max(mn[p<<1],tag[p]);
mn[p<<1|1]=max(mn[p<<1|1],tag[p]);
tag[p<<1]=max(tag[p<<1],tag[p]);
tag[p<<1|1]=max(tag[p<<1|1],tag[p]);
tag[p]=0;
}
void change(int p,int l,int r,int x,int y,int v){
if(x<=l&&y>=r){
tag[p]=max(tag[p],v);
mn[p]=max(mn[p],v);
return;
}
pushdown(p);
int mid=l+r>>1;
if(x<=mid)change(p<<1,l,mid,x,y,v);
if(y>mid)change(p<<1|1,mid+1,r,x,y,v);
update(p);
}
int query(int p,int l,int r,int x,int y){
if(x<=l&&y>=r)return mn[p];
int mid=l+r>>1,ret=1e9;
pushdown(p);
if(x<=mid)ret=min(ret,query(p<<1,l,mid,x,y));
if(y>mid)ret=min(ret,query(p<<1|1,mid+1,r,x,y));
return ret;
}
int hs0(int l,int r){return s0[r]-s0[l-1]*pw[r-l+1];}
int hs1(int l,int r){return s1[l]-s1[r+1]*pw[r-l+1];}
bool check(int l,int r){int mid=l+r>>1;return hs0(l,mid)==hs1(mid+1,r);}
int main(){
freopen("pass.in","r",stdin);
freopen("pass.out","w",stdout);
n=read();scanf("%s",s+1);
pw[0]=1;
for(int i=1;i<=n;i++)pw[i]=pw[i-1]*B;
for(int i=1;i<=n;i++)s0[i]=s0[i-1]*B+(ull)(s[i]-'a'+1);
for(int i=n;i>=1;i--)s1[i]=s1[i+1]*B+(ull)(s[i]-'a'+1);
scanf("%d",&q);
for(int i=1;i<=q;i++){
int l,r;l=read();r=read();
qr[r].push_back(pii(l,i));
}int L=2e4;
for(int i=1;i<=n;i++){
if(i>=3&&s[i]==s[i-2])add(i-2);
for(int j=i-1;j>=max(1,i-L);j-=2)
if(check(j,i)){change(1,1,n,j,i,j);break;}
for(auto v:qr[i]){
ans[v.se]=ask(i-1)-ask(v.fi-1);
if(!ans[v.se])ans[v.se]=query(1,1,n,v.fi,i)>=v.fi;
}
}
for(int i=1;i<=q;i++)printf("%d",ans[i]);
puts("");
return 0;
}
T3 膜拜大丹
不难发现只选二元环即可。并且倒序选肯定最优。
知道这两个结论后直接用 \(set\) 模拟即可。
题解做法非常难想到
首先我们是可以用二分图匹配暴力解决原问题的,考虑将问题简化到坐标轴上
先在图上标出 \((i,a_i)\) 和 \((j,b_j)\) ,然后引一条线落到 \(x\) 或 \(y\) 轴上。
那么 \(i,j\) 有边当前仅当 两个点对应的直线有交,如下图所示 (图是嫖的题解的)。
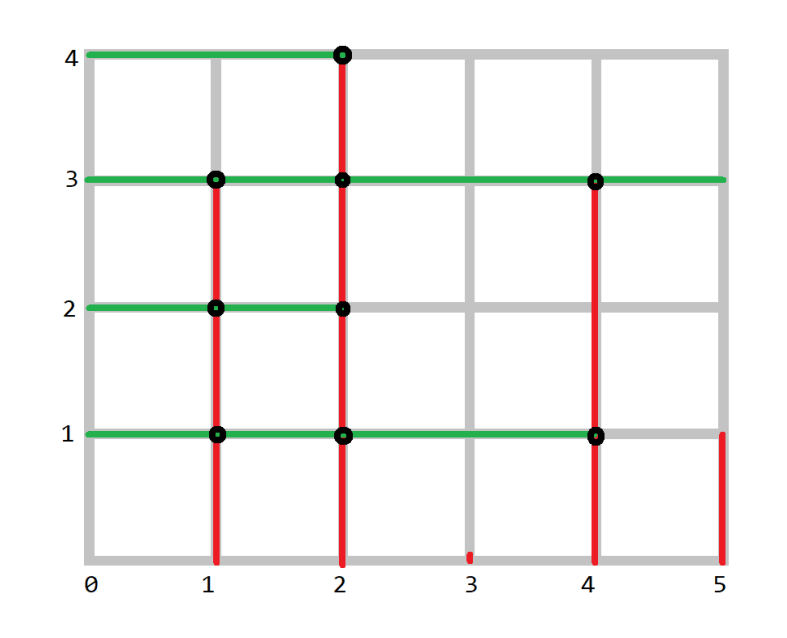
最大匹配不好求,求最大独立集(这个转换有点nb)。
那么问题的答案转化为:
在 \((i,a_i)\) 放一个点权为 \(c_i\) 的红点,在 \((b_j,j)\) 放一个点权为 \(c_j\) 的红点。那么在所有从左下角格子只能向右向上走走到右上角的外面的方案中,只保留路径上方的绿点点权和路径下方的红点点权的点权和的最大值。如下图所示
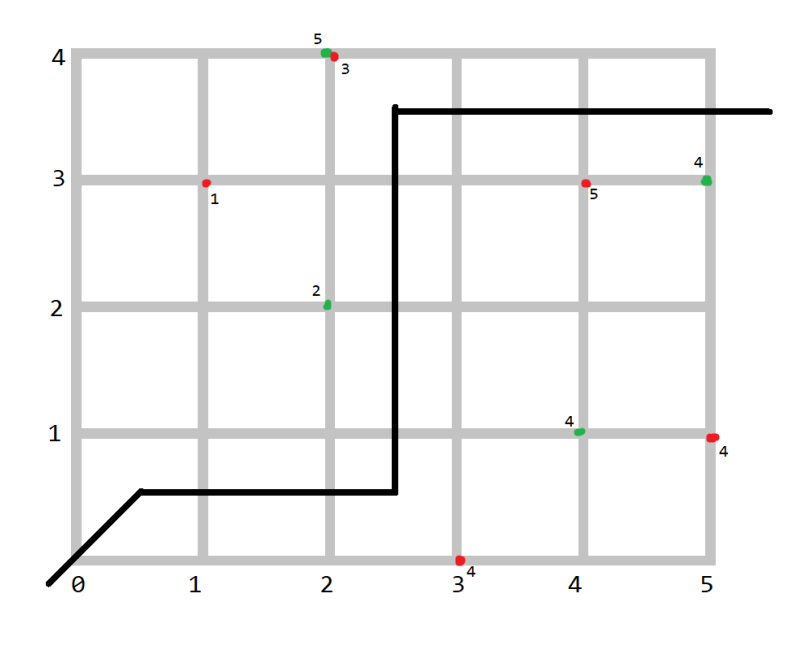
此时可以写出如下的dp式子:
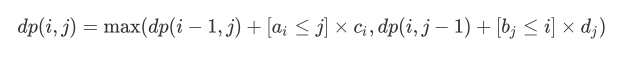
考虑优化 dp 的过程,发现如果钦定了一些红点被选择,那么贴着这些红点走一定是最优的,因为这样
会保留尽可能多的绿点(如下图贴着红点走)。
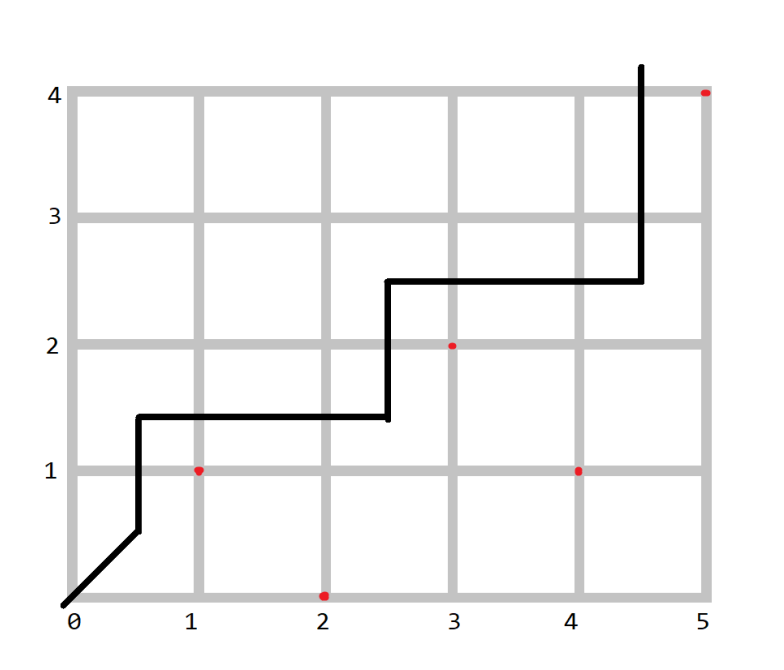
然后写出下列式子:
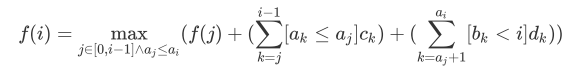
改写一下方程
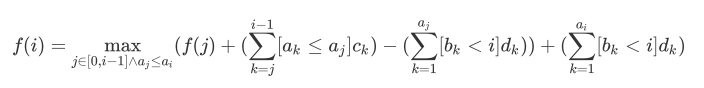
线段树加树状数组维护即可,时间复杂度 \(O(n \log_2 n)\)。
我写的是出题人题解的做法,后面发现有选手写了上面提及的第一种做法,感觉题解那个太难想到了。
Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int a[N],b[N],c[N],d[N],f[N];
int t[N],n,m;
void add(int x,int v){for(;x<=m;x+=x&-x)t[x]+=v;}
int ask(int x){int S=0;for(;x;x-=x&-x)S+=t[x];return S;}
int tag[N<<2],mx[N<<2];
void update(int p){mx[p]=max(mx[p<<1],mx[p<<1|1]);}
void pushdown(int p){
if(!tag[p])return;
mx[p<<1]+=tag[p];mx[p<<1|1]+=tag[p];
tag[p<<1]+=tag[p];tag[p<<1|1]+=tag[p];
tag[p]=0;
}
void modify(int p,int l,int r,int x,int y,int v){
if(x<=l&&r<=y){mx[p]+=v;tag[p]+=v;return;}
pushdown(p);
int mid=l+r>>1;
if(x<=mid)modify(p<<1,l,mid,x,y,v);
if(y>mid)modify(p<<1|1,mid+1,r,x,y,v);
update(p);
}
int qry(int p,int l,int r,int x,int y){
if(x<=l&&r<=y)return mx[p];
pushdown(p);
int mid=(l+r)>>1,ret=0;
if(x<=mid)ret=max(ret,qry(p<<1,l,mid,x,y));
if(y>mid)ret=max(ret,qry(p<<1|1,mid+1,r,x,y));
return ret;
}
void change(int p,int l,int r,int x,int v){
if(l==r){mx[p]=max(mx[p],v);return;}
pushdown(p);
int mid=l+r>>1;
if(x<=mid)change(p<<1,l,mid,x,v);
else change(p<<1|1,mid+1,r,x,v);
update(p);
}
vector<int>pos[N];
signed main(){
freopen("worship.in","r",stdin);
freopen("worship.out","w",stdout);
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=1;i<=m;i++){
scanf("%lld",&b[i]);
pos[b[i]+1].push_back(i);
}
long long ans=0;
for(int i=1;i<=n;i++){scanf("%lld",&c[i]);ans+=c[i];}
for(int i=1;i<=m;i++){scanf("%lld",&d[i]);ans+=d[i];}
a[++n]=m;
for(int i=1;i<=n;i++){
for(int j:pos[i])modify(1,0,m,j,m,-d[j]),add(j,d[j]);
f[i]=ask(a[i])+qry(1,0,m,0,a[i]);
change(1,0,m,a[i],f[i]-ask(a[i]));
modify(1,0,m,a[i],m,c[i]);
}
printf("%lld\n",ans-f[n]);
return 0;
}
Day 4
T1 我醉
先二分答案,然后点分治,每次在长链处统计跨过分治中心的答案,短链的长度可以直接算出来。然后再判断长链截去一个短链的后缀后形成的部分是否是一个回文串即可。分别用 字符串 \(hash\) 和 \(hash\) 表解决即可,时间复杂度 \(O(n\log_2^2n)\)
Code
#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int N=1e5+5,mod=3e5+5,INF=1e9;
int n,len;
int head[N],nxt[N<<1],to[N<<1],edge[N<<1],tot;
void add(int x,int y,int z){
nxt[++tot]=head[x];head[x]=tot;
to[tot]=y;edge[tot]=z;
}
int me[N],siz[N],ns,rt;
bool vis[N];
struct HashTable{
int head[mod+5],nxt[N],le[N];
int tot;ull to[N];
vector<int>tt;
void cl(){memset(head,tot=0,sizeof(head));tt.clear();}
void rset(){for(auto v:tt)head[v]=0;tot=0;tt.clear();}
void ins(ull x,int L){
int k=x%mod;
for(int i=head[k];i;i=nxt[i])
if(to[i]==x&&le[i]==L)return;
if(!head[k])tt.push_back(k);
nxt[++tot]=head[k];head[k]=tot;to[tot]=x;le[tot]=L;
}
bool qry(ull x,int L){
int k=x%mod;
for(int i=head[k];i;i=nxt[i])
if(to[i]==x&&le[i]==L)return 1;
return 0;
}
}M;
void findrt(int u,int F){
me[u]=0;siz[u]=1;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==F||vis[v])continue;
findrt(v,u);
siz[u]+=siz[v];
me[u]=max(me[u],siz[v]);
}
me[u]=max(me[u],ns-siz[u]);
//printf("me[%d] = %d\n",u,me[u]);
if(me[u]<me[rt])rt=u;
}
const ull B=193;
ull pw[N],val1[N],val2[N];
bool flag=0;
void Cnt(int u,int F,int dep,ull ch){
if(dep>len)return;
val1[dep]=val1[dep-1]*B+ch;
val2[dep]=val2[dep-1]+pw[dep-1]*ch;
if(len<=2*dep){
int tmp=val1[dep]-val1[2*dep-len]*pw[len-dep];
if(M.qry(tmp,len-dep)){
if(len%2==0){
int t1=2*dep-len,t2=t1/2;
if(val2[t2]==val1[t1]-val1[t2]*pw[t2])flag=1;
}
else{
int t1=2*dep-len,t2=t1/2;
if(val2[t2]==val1[t1]-val1[t2+1]*pw[t2])flag=1;
}
}
}
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==F||vis[v])continue;
Cnt(v,u,dep+1,edge[i]);
}
}
void Get(int u,int F,int dep,int vl){
if(dep>len/2)return;
M.ins(vl,dep);
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==F||vis[v])continue;
Get(v,u,dep+1,vl*B+edge[i]);
}
}
int tp[N];
void solve(int u){
vis[u]=1;int kk=0;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(vis[v])continue;
tp[++kk]=i;
Cnt(v,u,1,(ull)edge[i]),Get(v,u,1,(ull)edge[i]);
}
M.rset();
for(int i=kk;i>=1;i--){
int v=to[tp[i]];
Cnt(v,u,1,(ull)edge[tp[i]]),Get(v,u,1,(ull)edge[tp[i]]);
}
M.rset();
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(vis[v])continue;
me[rt=0]=INF;ns=siz[v];
findrt(v,u);solve(rt);
}
}
bool check(int x){
memset(vis,0,sizeof(vis));
M.cl();len=x;flag=0;
me[rt=0]=INF;ns=n;
findrt(1,0);
solve(rt);
return flag;
}
int main(){
freopen("name.in","r",stdin);
freopen("name.out","w",stdout);
scanf("%d",&n);
for(int i=1,u,v,l;i<n;i++){
scanf("%d%d%d",&u,&v,&l);
add(u,v,l);add(v,u,l);
}
int ans=1;
int l=1,r=(n-1)/2;
pw[0]=1;
for(int i=1;i<=n;i++)pw[i]=pw[i-1]*B;
while(l<=r){
int mid=l+r>>1;
if(check(2*mid))l=mid+1;
else r=mid-1;
}
ans=max(ans,2*r);
l=1,r=(n-1)/2;
while(l<=r){
int mid=l+r>>1;
if(check(2*mid+1))l=mid+1;
else r=mid-1;
}
ans=max(ans,2*r+1);
printf("%d\n",ans);
return 0;
}
T2 梧桐依旧
Burnside引理 + 行列式,不会
T3 卿且去
题解用 \(Dilworth\) 定理证的结论,感觉没这个必要而且不直观。
考虑如果 \(x \in T\) 且 \(2x \le n\) 那么很显然 \(2x \in T\),此时 \(x\) 就没用了。
而且对于 \(\forall x,x \in [n/2+1,n]\) 是互不成倍数关系的,所以我们只要知道 \(x \in [n/2+1,n]\) 在所有 \(S\) 的出现次数即可。设 \(\pi(n)\) 表示 \(n\) 以内的质因子数量,\(\omega(x)\) 表示 \(x\) 的质因子种类数, 答案就是
不难发现 \(2 ^ {\omega(x)}\) 是积性函数,套个min_25板子就好了。
Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353,inv2=(mod+1)>>1;
const int N=2e5+5;
int P[N],vis[N],tot;
void euler(int n){
for(int i=2;i<=n;i++){
if(!vis[i])vis[i]=i,P[++tot]=i;
for(int j=1;j<=tot&&P[j]*i<=n;j++){
if(vis[i]<P[j])break;
vis[i*P[j]]=P[j];
}
}
}
int f[N],val[N],maxv,T,n;
int g[N],ind1[N],ind2[N];
int get(int x){return x<=T?ind1[x]:ind2[n/x];}
void solveg(){
for (int l=1,r;l<=n;l=r+1){
int tmp=n/l;
r=min(n,n/tmp);
val[++maxv]=tmp;
g[maxv]=tmp-1;
if(tmp<=T)ind1[tmp]=maxv;
else ind2[r]=maxv;
}
for(int k=1;k<=tot;k++)
for (int j=1;j<=maxv&&P[k]*P[k]<=val[j];j++)
g[j]-=g[get(val[j]/P[k])]-(k-1);
}
int solvef(int x,int k){
if (P[k]>=x||k>tot)return 0;
int id=get(x),ans=1LL*(g[id]-k)*inv2%mod;
for(int i=k+1;i<=tot&&P[i]*P[i]<=x;i++)
for(int pc=P[i];pc<=x;pc*=P[i])
ans=(ans+inv2*(solvef(x/pc,i)+(pc!=P[i])))%mod;
return ans;
}
int fpow(int a,int b){
int ret=1;
for(;b;b>>=1){
if(b&1)ret=1LL*ret*a%mod;
a=1LL*a*a%mod;
}return ret;
}
signed main(){
freopen("yyds.in","r",stdin);
freopen("yyds.out","w",stdout);
cin>>n;T=sqrt(n);
euler(T+1);solveg();
int tmp=fpow(2,g[1]);
int ans1=solvef(n,1),ans2=(solvef(n/2,1)*inv2+inv2)%mod;
int ans=(((n-1)>>1)%mod*tmp%mod+tmp*(ans2-ans1))%mod;
cout<<(ans+mod)%mod<<endl;
return 0;
}
Day 5
T1 下落的数字
首先父亲到每个儿子都对应一段值域区间,先树剖,用线段树维护每条重链的区间交,在线段树上二分可以知道最远可以跳到哪,然后再用 \(set\) 查询跳到哪个轻儿子。最多跳 \(O(\log2_n)\) 次,总复杂度 \(O(n\log_2^2n)\)。
Code
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5,INF=1e9;
vector<int>G[N];
set<pii>st[N];
map<int,int>ss;
int w[N],n,m;
int dep[N],fa[N],siz[N],son[N],L[N],R[N];
int dfn[N],rnk[N],idx,top[N],dn[N];
void dfs0(int u,int F){
dep[u]=dep[fa[u]=F]+1;
siz[u]=1;int pr=0;
for(auto v:G[u]){
if(v==F)continue;
dfs0(v,u);siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
R[v]=w[v];L[v]=w[pr]+1;pr=v;
}
}
void dfs1(int u,int Tp){
dn[Tp]=u;dfn[u]=++idx;rnk[idx]=u;top[u]=Tp;
if(son[u])dfs1(son[u],Tp);
for(auto v:G[u])if(v!=fa[u]&&v!=son[u])dfs1(v,v);
}
int lg[N<<2],rg[N<<2],sl[N<<2],sr[N<<2];
void update(int p){
lg[p]=max(lg[p<<1],lg[p<<1|1]);
rg[p]=min(rg[p<<1],rg[p<<1|1]);
}
void build(int p,int l,int r){
sl[p]=l;sr[p]=r;
if(l==r){lg[p]=L[rnk[l]];rg[p]=R[rnk[l]];return;}
int mid=l+r>>1;
build(p<<1,l,mid);build(p<<1|1,mid+1,r);
update(p);
}
void change(int p,int l,int r,int x,int lv,int rv){
if(l==r){lg[p]=lv;rg[p]=rv;return;}
int mid=l+r>>1;
if(x<=mid)change(p<<1,l,mid,x,lv,rv);
else change(p<<1|1,mid+1,r,x,lv,rv);
update(p);
}
int sk[N],tp;
void find(int p,int l,int r,int x,int y){
if(x<=l&&y>=r){sk[++tp]=p;return;}
int mid=l+r>>1;
if(x<=mid)find(p<<1,l,mid,x,y);
if(y>mid)find(p<<1|1,mid+1,r,x,y);
}
int qry(int p,int l,int r,int x){
if(l==r){
if(lg[p]<=x&&x<=rg[p])return rnk[l];
else return rnk[l-1];
}
int mid=l+r>>1;
if(lg[p<<1]<=x&&x<=rg[p<<1])return qry(p<<1|1,mid+1,r,x);
else return qry(p<<1,l,mid,x);
}
int Get(int u,int x){
tp=0;int nl=1,nr=INF;
//cout<<u<<' '<<dn[u]<<' '<<x<<endl;
//cout<<dfn[u]<<' '<<dfn[dn[u]]<<endl;
find(1,1,n,dfn[u],dfn[dn[u]]);
for(int i=1;i<=tp;i++){
int p=sk[i];
nl=max(nl,lg[p]),nr=min(nr,rg[p]);
//printf("query %d : %d %d\n",i,nl,nr);
if((!(nl<=x&&x<=nr))||nl>nr||i==tp){
//cout<<"cao !!! "<<p<<' '<<sl[p]<<' '<<sr[p]<<' '<<x<<endl;
return qry(p,sl[p],sr[p],x);
}
}
return u;
}
int query(int x){
int u=1;
while(true){
int v=Get(u,x);
auto now=st[v].lower_bound(pii(x,0));
if(now==st[v].end())return v;
else u=(*now).se;
}
}
void fuck(int p,int l,int r){
// cout<<p<<' '<<lg[p]<<' '<<rg[p]<<' '<<l<<' '<<r<<endl;
if(l==r)return;
int mid=l+r>>1;
fuck(p<<1,l,mid);fuck(p<<1|1,mid+1,r);
}
bool cmp(int x,int y){return w[x]<w[y];}
int main(){
freopen("fall.in","r",stdin);
freopen("fall.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&w[i]),ss[w[i]]++;
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
G[u].push_back(v);G[v].push_back(u);
}
for(int i=1;i<=n;i++)sort(G[i].begin(),G[i].end(),cmp);
dfs0(1,0);dfs1(1,1);
// cout<<siz[2]<<' '<<siz[7]<<' '<<siz[9]<<' '<<siz[2]+siz[7]+siz[9]+1<<endl;
L[1]=1;R[1]=INF;
//for(int i=1;i<=n;i++)if(L[i]!=1)cout<<i<<' '<<L[i]<<' '<<R[i]<<endl;
build(1,1,n);
for(int u=1;u<=n;u++)
for(auto v:G[u])if(v!=fa[u])st[u].insert(pii(w[v],v));
//cout<<"dfn "<<dfn[2]<<' '<<dfn[3]<<endl;
tp=0;find(1,1,n,dfn[2],dfn[3]);int nl=1,nr=INF;
for(int i=1;i<=tp;i++){
int p=sk[i];
nl=max(nl,lg[p]),nr=min(nr,rg[p]);
//if((!(nl<=x&&x<=nr))||nl>nr)return qry(p,sl[p],sr[p],x);
}//cout<<nl<<' '<<nr<<' '<<tp<<" fff"<<endl;
while(m--){
int op,a,b;
scanf("%d%d",&op,&a);
if(op==1){
scanf("%d",&b);
if(a==1)continue;
int F=fa[a];
auto now=++st[F].lower_bound(pii(w[a],a));
if(now!=st[F].end()){
auto cur=st[F].lower_bound(pii(w[a],a));
if(cur!=st[F].begin())change(1,1,n,dfn[(*now).se],(*--cur).fi+1,(*now).fi);
else change(1,1,n,dfn[(*now).se],1,(*now).fi);
}
st[F].erase(pii(w[a],a));w[a]=b;st[F].insert(pii(w[a],a));
now=st[F].lower_bound(pii(w[a],a));
if(now==st[F].begin())change(1,1,n,dfn[a],1,w[a]);
else change(1,1,n,dfn[a],(*--now).fi+1,w[a]);
now=st[F].upper_bound(pii(w[a],INF));
if(now!=st[F].end())change(1,1,n,dfn[(*now).se],w[a]+1,(*now).fi);
}else printf("%d\n",query(a));
}
return 0;
}
T2 序排速快
T3 树
Day 6
T1 一般图带权多重匹配
先考虑 \(a_i\) 全是偶数的情况。把操作看成在图上加一条边,那么原图一定存在欧拉回路。
思考一下欧拉回路的实现,我们必定能把每个点的边分为一半出度一半入度,此时网络流建模就很显然了:
\(1\) . \(add(S,i_1,\frac{a_i}{2},0)\)
\(2\) . \(add(i_2,T,\frac{a_i}{2},0)\)
\(3\) . \(add(i1,j2,inf,c_{i,j})\)
那么因为奇数最多 \(10\) 个 ,直接 \(2^{10}\) 枚举是出度还是入度。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+5,M=2e5+5,INF=2e9;
int head[N],nxt[M],to[M],tot=1;
int edge[M],cst[M],ans0,ans1;
void add(int x,int y,int z,int w){
nxt[++tot]=head[x];head[x]=tot;
to[tot]=y;edge[tot]=z;cst[tot]=w;
nxt[++tot]=head[y];head[y]=tot;
to[tot]=x;edge[tot]=0;cst[tot]=-w;
}
int incf[N],dis[N],vis[N],pre[N];
queue<int>q;
bool spfa(int s,int t){
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
vis[s]=1;q.push(s);dis[s]=0;incf[s]=INF;
while(q.size()){
int u=q.front();q.pop();
vis[u]=0;
for(int i=head[u];i;i=nxt[i])
if(edge[i]>0&&dis[to[i]]>dis[u]+cst[i]){
int v=to[i];
dis[v]=dis[u]+cst[i];
incf[v]=min(incf[u],edge[i]);
pre[v]=i;
if(vis[v])continue;
vis[v]=1;q.push(v);
}
}if(dis[t]>1e9)return 0;
return 1;
}
void update(int s,int t){
int u=t;
while(u!=s){
int i=pre[u];
edge[i]-=incf[t];
edge[i^1]+=incf[t];
u=to[i^1];
}
ans0+=incf[t];
ans1+=dis[t]*incf[t];
}
void EK(int s,int t){while(spfa(s,t))update(s,t);}
const int MX=55;
int n,m,a[MX],b[MX][MX];
signed main(){
freopen("match.in","r",stdin);
freopen("match.out","w",stdout);
int s=0,t=N-1,sum=0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
sum+=a[i];m+=(a[i]&1);
}
if(sum&1)return puts("-1"),0;
int ret=2e9;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)scanf("%d",&b[i][j]);
for(int S=0;S<(1<<m);S++){
memset(head,0,sizeof(head));
tot=1;ans0=ans1=0;int tmp=0;
for(int i=1;i<=n;i++){
tmp+=(a[i]&1);
int c1=a[i]/2+(a[i]%2==1?((S>>(tmp-1))&1):0),c2=a[i]-c1;
add(s,i,c1,0);add(i+n,t,c2,0);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
add(i,j+n,INF,b[i][j]);
EK(s,t);
if(ans0*2==sum)ret=min(ret,ans1);
}
printf("%d\n",ret);
return 0;
}
T2 排序
T3 传染
暴力做法:枚举两个点直接连边,跑个强联通分量求出所有的零入度点个数就是答案。
考虑用点分治加前缀优化建图来优化建边。
每次只考虑跨过分治中心的连边,按节点到分治中心的距离排序。
那么每个点连向的必定是一段前缀。前缀优化建图即可。
点数和边数都是 \(O(n\log_2n)\) 级别的,时间复杂度 \(O(n \log_2^2n)\) 赛时写这个很大概率被卡常。
有一个隐式建图的做法常数很小,感兴趣的可以思考一下。。
Code
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=3e5+5,W=20,INF=1e18;
int n,m,r[N];
int head[N],to[N<<1],nxt[N<<1],edge[N<<1],tot;
void add(int x,int y,int z){
nxt[++tot]=head[x];head[x]=tot;
to[tot]=y;edge[tot]=z;
}
int me[N],siz[N],rt,ns;bool vis[N];
void findrt(int u,int F){
siz[u]=1;me[u]=0;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==F||vis[v])continue;
findrt(v,u);siz[u]+=siz[v];
me[u]=max(me[u],siz[v]);
}
me[u]=max(me[u],ns-siz[u]);
if(me[u]<me[rt])rt=u;
}
vector<int>G[N*W];
pii s[N];int num;
void get(int u,int F,int dis){
s[++num]=pii(dis,u);
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==F||vis[v])continue;
get(v,u,dis+edge[i]);
}
}
void work(int u){
num=0;get(u,0,0);
sort(s+1,s+num+1);
int mx=0,pr=m;
for(int i=1;i<=num;i++)mx=max(r[s[i].se]-s[i].fi,mx);
for(int i=1;i<=num;i++){
if(s[i].fi>mx)break;
G[++m].push_back(s[i].se);
}
m=pr+1;
for(int i=2;i<=num;i++){
if(s[i].fi>mx)break;
m++;G[m].push_back(m-1);
}
for(int i=1;i<=num;i++){
int pos=upper_bound(s+1,s+num+1,pii(r[s[i].se]-s[i].fi,INF))-s-1;
if(pos!=0)G[s[i].se].push_back(pr+pos);
}
}
void solve(int u){
vis[u]=1;work(u);
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(vis[v])continue;
me[rt=0]=INF;ns=siz[v];findrt(v,u);solve(rt);
}
}
int dfn[N*W],low[N*W],col[N*W],vs[N*W],idx,cnt;
int sk[N*W],top;
void tarjan(int u){
low[u]=dfn[u]=++idx;
vs[sk[++top]=u]=1;
for(auto v:G[u])
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(vs[v])
low[u]=min(low[u],dfn[v]);
if(dfn[u]==low[u]){
cnt++;int v;
do{
v=sk[top--];
vs[v]=0;
col[v]=cnt;
}while(u!=v);
}
}
int in[N*W];
signed main(){
freopen("infect.in","r",stdin);
freopen("infect.out","w",stdout);
scanf("%lld",&n);m=n;
for(int i=1;i<=n;i++)scanf("%lld",&r[i]);
for(int i=1,x,y,z;i<n;i++){
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,z);add(y,x,z);
}
me[rt=0]=INF;ns=n;findrt(1,0);solve(rt);
for(int i=1;i<=m;i++)if(!dfn[i])tarjan(i);
for(int u=1;u<=m;u++)
for(auto v:G[u])if(col[u]!=col[v])in[col[v]]++;
int ans=0;
for(int i=1;i<=cnt;i++)ans+=(in[i]==0);
printf("%lld\n",ans);
return 0;
}
Day 7
T1 好
首先题目这个约束条件可以转化成每次删一个先升后降的差为 \(1\) 序列。
可以直接 \(O(n^4)\) 暴力区间 \(dp\)。
考虑到 \(l,r\) 两个位置如果没有同时被删除那么 \(a_l\) 和 \(a_r\) 本身就是可以独立转移的。
所以只考虑 \(a_l\) 和 \(a_r\) 同时被删除,那么就很简单了。
设 \(l_{i,j}\) 表示从 \(i\) 删到 \(j\) 升序可以划分出的 \(f\) 的最大值。\(r_{i,j}\) 则是降序
时间复杂度 \(O(n^3)\)
Code
#include<bits/stdc++.h>
using namespace std;
const int N=410,INF=1e9;
int val[N],a[N],n;
int f[N][N],l[N][N],r[N][N],ret[N];
int main(){
freopen("good.in","r",stdin);
freopen("good.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&val[i]);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)f[i][j]=l[i][j]=r[i][j]=-INF;
for(int i=1;i<=n;i++)l[i][i]=r[i][i]=f[i][i-1]=0,f[i][i]=val[1];
for(int len=2;len<=n;len++)
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
for(int k=i;k<j;k++){
if(a[k]+1==a[j])
l[i][j]=max(l[i][j],l[i][k]+f[k+1][j-1]);
if(a[k]-1==a[j])
r[i][j]=max(r[i][j],r[i][k]+f[k+1][j-1]);
f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]);
}
for(int k=i;k<=j;k++)
f[i][j]=max(f[i][j],l[i][k]+r[k][j]+val[2*a[k]-a[i]-a[j]+1]);
}
for(int i=1;i<=n;i++){
ret[i]=ret[i-1];
for(int j=0;j<i;j++)
ret[i]=max(ret[i],ret[j]+f[j+1][i]);
}
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,ret[i]);
printf("%d\n",ans);
return 0;
}
T2 色
结论:答案是最小生成树上一条边的边权。
开三种不同的 \(set\),分别维护
1.一个点儿子节点每个颜色的集合.
2.每个颜色(除当前颜色外)离他最近的儿子点集合.
3.全局的答案。
模拟即可。
Code
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5,M=3e5+5;
int n,m,c,q;
struct Edge{int x,y,v;}e[M];
bool cmp(Edge a,Edge b){return a.v<b.v;}
vector<pii>G[N];
int fa[N];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
int val[N],col[N];
multiset<int>mn[N],all;
map<int,multiset<int> >s[N];
void dfs(int u,int F){
fa[u]=F;
for(auto p:G[u]){
if(p.fi==F)continue;
int v=p.fi;val[v]=p.se;
if(col[u]!=col[v]&&s[u][col[v]].size())mn[u].erase(mn[u].find(*s[u][col[v]].begin()));
s[u][col[v]].insert(p.se);
if(col[u]!=col[v])mn[u].insert(*s[u][col[v]].begin());
dfs(v,u);
}if(mn[u].size())all.insert(*mn[u].begin());
}
int main(){
freopen("color.in","r",stdin);
freopen("color.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&c,&q);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].v);
for(int i=1;i<=n;i++)scanf("%d",&col[i]);
sort(e+1,e+m+1,cmp);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int x=find(e[i].x),y=find(e[i].y);
if(x==y)continue;
fa[x]=y;
G[e[i].x].push_back(pii(e[i].y,e[i].v));
G[e[i].y].push_back(pii(e[i].x,e[i].v));
}
dfs(1,0);
while(q--){
int x,v;
scanf("%d%d",&x,&v);
int p=fa[x];
if(x!=1){
if(mn[p].size())all.erase(all.find(*mn[p].begin()));
if(col[p]!=col[x]&&s[p][col[x]].size())mn[p].erase(mn[p].find(*s[p][col[x]].begin()));
s[p][col[x]].erase(s[p][col[x]].find(val[x]));
if(col[p]!=col[x]&&s[p][col[x]].size())mn[p].insert(*s[p][col[x]].begin());
if(col[p]!=v&&s[p][v].size())mn[p].erase(mn[p].find(*s[p][v].begin()));
s[p][v].insert(val[x]);
if(col[p]!=v&&s[p][v].size())mn[p].insert(*s[p][v].begin());
if(mn[p].size())all.insert(*mn[p].begin());
}
if(mn[x].size())all.erase(all.find(*mn[x].begin()));
if(s[x][col[x]].size())mn[x].insert(*s[x][col[x]].begin());
if(s[x][v].size())mn[x].erase(mn[x].find(*s[x][v].begin()));
if(mn[x].size())all.insert(*mn[x].begin());
col[x]=v;
printf("%d\n",*all.begin());
}
return 0;
}
T3 乐
分治 NTT,不会
Day 8
T1 开心消消乐
较简单的 dp套dp 。 一般dp套dp的难点在于内层的设计,大多数的内层dp都是判合法性。
所以我们考虑如何判断合法性。我们把两位看成一组,把两位分成同时合并和不同时合并两种情况。
所以压入序列后返回的颜色可以看成一个函数 \(G[a,b](x)\) 表示 \(x=0\) 时返回 \(a\),\(x=1\) 时返回 \(b\)。
显然 \(G\) 只有 \(4\) 种本质不同的取值,于是直接 \(dp\) 就好了。时间复杂度 \(O(2^{2^2}n)\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define calc(a,b,c) (T[(((a)<<2)|((b)<<1)|(c))]-'0')
const int N=1e5+10,mod=998244353;
char T[8],s[N];
bool tmp[2][2];
int f[N][1<<4],To[1<<4][1<<4];
int to(int A,int B) {
if(To[A][B]!=-1)return To[A][B];
memset(tmp,0,sizeof(tmp));
int a1=B&1,a2=B>>1,cnt=0,C=0;
for(int i=0;i<2;i++)
for(int j=0;j<2;j++){
if(!(A>>(cnt++)&1))continue;
tmp[calc(0,a2,a1?j:i)][calc(1,a2,a1?j:i)]=1;
tmp[calc(0,a2,a1)?j:i][calc(1,a2,a1)?j:i]=1;
}
cnt=0;
for(int i=0;i<2;i++)
for(int j=0;j<2;j++){if(tmp[i][j])C|=1<<cnt;cnt++;}
return To[A][B]=C;
}
int main(){
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
int TT;scanf("%d",&TT);
while(TT--){
scanf("%s%s",T,s+1);
int n=strlen(s+1);
memset(f,0,sizeof(f));
memset(To,-1,sizeof(To));
f[0][2]=1;
for(int i=1;i<n;i+=2){
for(int j=0;j<4;j++){
if(s[i]!='?'&&s[i]-'0'!=(j&1))continue;
if(s[i+1]!='?'&&s[i+1]-'0'!=(j>>1))continue;
for(int k=0;k<1<<4;k++) {
if(!f[i-1][k])continue;
int t=to(k,j);
f[i+1][t]=(f[i+1][t]+f[i-1][k])%mod;
}
}
}
int ans=0;
if(s[n]=='?'||s[n]=='0')
for(int i=0;i<1<<4;i++)
if((i>>2&1)||(i>>3&1))ans=(ans+f[n-1][i])%mod;
if(s[n]=='?'||s[n]=='1')
for(int i=0;i<1<<4;i++)
if((i>>1&1)||(i>>3&1))ans=(ans+f[n-1][i])%mod;
printf("%d\n",ans);
}
return 0;
}
T2 树上的棋局
不难发现 \(sg_u\) 的值就是 \(u\) 子树离它最远的点到 \(u\) 的距离。答案就是所有有奇数个棋子的点的异或值。
这题的主要难点在于换根操作,但不难发现当换根为 \(u\) 时只有 \(1 \to x\) 这条路径上的点的 \(sg\) 值发生改变。
考虑用树链剖分维护这个操作,类似于动态dp的实现,我们预处理一个 \(fsg_u\) 表示当 \(u\) 为根时 \(fa_u\) 的 \(sg\) 值,每次跳重链查即可。
考虑修改操作,用线段树很好维护,显然路径的修改与根无关,子树修改也很简单,讨论一下 \(v\) 和 \(rt\) 的位置关系即可。
具体细节可以参见代码。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,rt;
vector<int>G[N];
int dep[N],siz[N],fa[N],son[N],mx[N][2];
int dfn[N],rnk[N],top[N],fsg[N],idx;
void dfs1(int u,int F){
dep[u]=dep[fa[u]=F]+(siz[u]=1);
for(auto v:G[u]){
if(v==F)continue;dfs1(v,u);
siz[u]+=siz[v];if(siz[v]>siz[son[u]])son[u]=v;
if(mx[v][0]+1>mx[u][0])mx[u][1]=mx[u][0],mx[u][0]=mx[v][0]+1;
else if(mx[v][0]+1>mx[u][1])mx[u][1]=mx[v][0]+1;
}
}
void dfs2(int u,int tp){
dfn[u]=++idx;rnk[idx]=u;top[u]=tp;
if(fa[u]>1)fsg[u]=max(fsg[u],fsg[fa[u]]+1);
for(auto v:G[u]){
if(v==fa[u])continue;
if(mx[v][0]+1==mx[u][0])fsg[v]=mx[u][1];
else fsg[v]=mx[u][0];
}
if(son[u])dfs2(son[u],tp);
for(auto v:G[u])if(v!=son[u]&&v!=fa[u])dfs2(v,v);
}
int tag[N<<2],sg[N<<2],asg[N<<2],hsg[N<<2],ahsg[N<<2];
void pushtag(int p){tag[p]^=1;sg[p]^=asg[p];hsg[p]^=ahsg[p];}
void pushdown(int p){if(!tag[p])return;tag[p]=0;pushtag(p<<1);pushtag(p<<1|1);}
void update(int p){
sg[p]=sg[p<<1]^sg[p<<1|1];asg[p]=asg[p<<1]^asg[p<<1|1];
hsg[p]=hsg[p<<1]^hsg[p<<1|1];ahsg[p]=ahsg[p<<1]^ahsg[p<<1|1];
}
void build(int p,int l,int r){
if(l==r){sg[p]=asg[p]=mx[rnk[l]][0];hsg[p]=ahsg[p]=fsg[son[rnk[l]]];return;}
int mid=l+r>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);update(p);
}
void change(int p,int l,int r,int x,int y){
if(x<=l&&y>=r){pushtag(p);return;}
int mid=l+r>>1;pushdown(p);
if(x<=mid)change(p<<1,l,mid,x,y);
if(y>mid)change(p<<1|1,mid+1,r,x,y);
update(p);
}
bool exsit(int p,int l,int r,int x){
if(l==r)return !tag[p];
int mid=l+r>>1;pushdown(p);
if(x<=mid)return exsit(p<<1,l,mid,x);
else return exsit(p<<1|1,mid+1,r,x);
}
int querysg(int p,int l,int r,int x,int y){
if(x>y)return 0;
if(x<=l&&y>=r)return sg[p];
int mid=l+r>>1,ret=0;pushdown(p);
if(x<=mid)ret^=querysg(p<<1,l,mid,x,y);
if(y>mid)ret^=querysg(p<<1|1,mid+1,r,x,y);
return ret;
}
int queryhsg(int p,int l,int r,int x,int y){
if(x>y)return 0;
if(x<=l&&y>=r)return hsg[p];
int mid=l+r>>1,ret=0;pushdown(p);
if(x<=mid)ret^=queryhsg(p<<1,l,mid,x,y);
if(y>mid)ret^=queryhsg(p<<1|1,mid+1,r,x,y);
return ret;
}
void Son(int v){
int u=rt;if(u==v){change(1,1,n,1,n);return;}
while(dep[u]>dep[v]&&top[u]!=top[v])u=fa[top[u]];
if(top[u]!=top[v]||dep[u]<dep[v]){change(1,1,n,dfn[v],dfn[v]+siz[v]-1);return;}
u=rt;
while(fa[u]!=v&&top[u]!=top[v]){u=top[u];if(fa[u]!=v)u=fa[u];}
if(top[u]==top[v])change(1,1,n,dfn[son[v]],dfn[son[v]]+siz[son[v]]-1);
else change(1,1,n,dfn[u],dfn[u]+siz[u]-1);
change(1,1,n,1,n);
}
void Path(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
change(1,1,n,dfn[top[u]],dfn[u]);
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
change(1,1,n,dfn[u],dfn[v]);
}
int solve(){
int ret=sg[1],u=rt;
while(u)ret^=querysg(1,1,n,dfn[top[u]],dfn[u]),u=fa[top[u]];u=rt;
if(exsit(1,1,n,dfn[u]))ret^=max(mx[u][0],u==1?0:fsg[u]+1);
while(top[u]!=1){
ret^=queryhsg(1,1,n,dfn[top[u]],dfn[u]-1);u=top[u];
if(exsit(1,1,n,dfn[fa[u]]))ret^=fsg[u];u=fa[u];
}
ret^=queryhsg(1,1,n,1,dfn[u]-1);
return ret;
}
int main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
scanf("%d%d",&n,&m);rt=1;
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
G[u].push_back(v);G[v].push_back(u);
}
dfs1(1,0);dfs2(1,1);build(1,1,n);
while(m--){
int op,u,v,x;
scanf("%d%d",&op,&u);
if(op==1){scanf("%d%d",&v,&x);Path(u,v);rt=x;}
else{scanf("%d",&x);Son(u);rt=x;}
printf("%d\n",solve());
}
return 0;
}
T3 社会黄油飞
我们把原式子化成 \(lim + V - lim|S| \le 0\)。
显然就是求一个点权为 \(-lim\) 边权为 \(1\) 的图的最大权闭合子图。
有个显然的暴力就是钦定必选的点跑 \(n\) 次 \(dinic\)。只要不连 \((i,t,lim)\) 这条边就行了。
因为数据水,暴力可以通过本题。
具体优化我们考虑每次退掉 \(i-1\) 的流,再重新改变边的限制,再次增广。
但事实上这个优化并不显著,也许还跑不过暴力,(于是我就用暴力艹过去了。)
有一个可以 AC 此题的贪心做法,但不知道是不是对的:每次选一个度数最大的点删掉,再更新其他点的度数。
也有人用不同的贪心做法拼起来拿到了可观的分数,所以说乱搞能力也是很重要的。
Code
#include<bits/stdc++.h>
#define INF (0x3f3f3f3f)
using namespace std;
const int N=2e4+5,M=2e6+5;
int s,t;
int nxt[M],to[M],edge[M],head[N],tot=1;
int d[N],cur[N];
queue<int>q;
void add(int x,int y,int z){
nxt[++tot]=head[x];head[x]=tot;
to[tot]=y;edge[tot]=z;
nxt[++tot]=head[y];head[y]=tot;
to[tot]=x;edge[tot]=0;
}
bool bfs(){
memset(d,-1,sizeof(d));
while(q.size())q.pop();
q.push(s);d[s]=0;
cur[s]=head[s];
while(q.size()){
int u=q.front(),v;q.pop();
for(int i=head[u];i;i=nxt[i])
if(d[v=to[i]]==-1&&edge[i]){
q.push(v);
d[v]=d[u]+1;
cur[v]=head[v];
if(v==t)return 1;
}
}return 0;
}
int dfs(int u,int lim){
if(u==t)return lim;
int fl=0;
for(int i=cur[u];i&&fl<lim;i=nxt[i]){
cur[u]=i;
int v=to[i];
if(edge[i]!=0&&d[v]==d[u]+1){
int k=dfs(v,min(edge[i],lim-fl));
if(!k)d[v]=-1;
edge[i]-=k;edge[i^1]+=k;
fl+=k;
}
}return fl;
}
int dinic(){
int flow=0,maxflow=0;
while(bfs())
while(flow=dfs(s,INF))
maxflow+=flow;
return maxflow;
}
int ea[N],eb[N];
int n,m,lim;
int main(){
freopen("socialbutterfly.in","r",stdin);
freopen("socialbutterfly.out","w",stdout);
scanf("%d%d%d",&n,&m,&lim);
s=N-1,t=N-2;
for(int i=1;i<=m;i++)cin>>ea[i]>>eb[i];
for(int i=1;i<=n;i++){
memset(head,0,sizeof(head));tot=1;
for(int j=1;j<=n;j++)if(j!=i)add(j,t,lim);
for(int k=1;k<=m;k++){
int u=ea[k],v=eb[k];
add(s,k+n,1);
add(k+n,u,INF);
add(k+n,v,INF);
}
if(m-dinic()>0)return puts("Yes"),0;
}
puts("No");
return 0;
}



