Link Cut Tree 学习笔记

前置废话

要会splay
Link-Cut Tree，简称LCT，但它不叫动态树，动态树是指一类问题。
lct干嘛用？动态维护一棵树的链和子树的各种信息

实链剖分

相较于重链剖分不同的是可以任意选择实儿子，而不是以子树大小为划分依据。
其他的概念和结构和重链剖分是一致的。
因为它灵活多变，所以我们用同样灵活多变splay来维护。

LCT！

我们先来看一看辅助树的一些性质，再通过一张图实际了解一下辅助树的具体结构。

在本文里，你可以认为一些 Splay 构成了一个辅助树，每棵辅助树维护的是一棵树，一些辅助树构成了 LCT，其维护的是整个森林。

辅助树由多棵 Splay 组成，每棵 Splay 维护原树中的一条路径，且中序遍历这棵 Splay 得到的点序列，从前到后对应原树“从上到下”的一条路径。

原树每个节点与辅助树的 Splay 节点一一对应。

辅助树的各棵 Splay 之间并不是独立的。每棵 Splay 的根节点的父亲节点本应是空，但在 LCT 中每棵 Splay 的根节点的父亲节点指向原树中这条链的父亲节点（即链最顶端的点的父亲节点）。这类父亲链接与通常 Splay 的父亲链接区别在于儿子认父亲，而父亲不认儿子，对应原树的一条虚边。因此，每个连通块恰好有一个点的父亲节点为空。

由于辅助树的以上性质，我们维护任何操作都不需要维护原树，辅助树可以在任何情况下拿出一个唯一的原树，我们只需要维护辅助树即可。

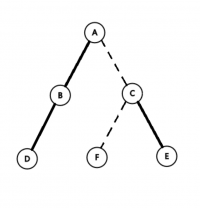
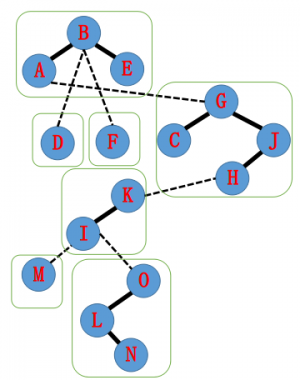
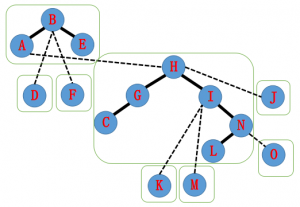
现在我们有一棵原树，如图。加粗边是实边，虚线边是虚边。

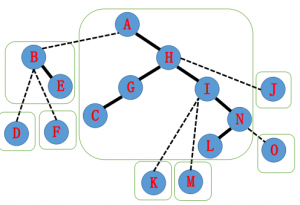
由刚刚的定义，辅助树的结构如下

以上摘自oiwiki

代码实现

我们以下面的例题来讲解lct的实现：
给定\(n\)个点，支持加边删边和查询两个点的距离(边权为\(1\))。

我们先定义一下变量：

int ch[N][2],f[N],rev[N],siz[N];
//左右儿子，父亲，翻转标子，子树大小(siz[x]:平衡树中以x为根的子树大小)。

一个简单函数，判断一个点是否是一个splay的根。
在前面我们已经说过，LCT 具有如果一个儿子不是实儿子，他的父亲找不到它的性质
所以当一个点既不是它父亲的左儿子，又不是它父亲的右儿子，它就是当前 Splay 的根

bool isrt(int x){return ch[f[x]][0]!=x&&ch[f[x]][1]!=x;}

更新信息

void clear(int x){ch[x][0]=ch[x][1]=f[x]=rev[x]=siz[x]=0;}
void pushup(int x){
   clear(0);if(!x)return;
   siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1;
}

平衡树翻转标记下传，等下会说到

void pushrev(int x){
    if(!x)return;
    rev[x]^=1;
    swap(ch[x][0],ch[x][1]);
}
void pushdown(int x){
    if(!rev[x])return;
    pushrev(ch[x][0]);
    pushrev(ch[x][1]);
    rev[x]=0;
}

splay函数，不多讲，有一句话不同，要注意：

int get(int x){return ch[f[x]][1]==x;}
void rotate(int x){
    int y=f[x],z=f[y],k=get(x);
    if(!isrt(y))ch[z][ch[z][1]==y]=x;//这一句注意要写在前面
    ch[y][k]=ch[x][k^1];f[ch[x][k^1]]=y;
    ch[x][k^1]=y;f[y]=x;f[x]=z;
    pushup(y);pushup(x);pushup(z);
}
void splay(int x){
    update(x);
    for(int fa;fa=f[x],!isrt(x);rotate(x))
        if(!isrt(fa))rotate(get(fa)==get(x)?fa:x);
}

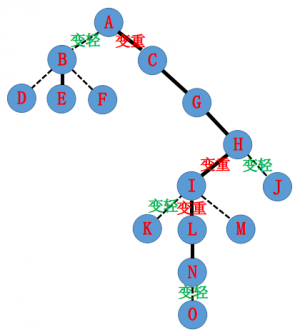
我们有这样一棵树，实线为实边，虚线为虚边。

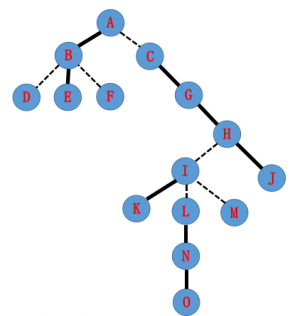
它的辅助树可能长成这样（构图方式不同可能 LCT 的结构也不同）。
每个绿框里是一棵 Splay。

现在我们要 \(Access(N)\), 把\(A\)到\(N\)路径上的边都变为实边，拉成一棵 Splay。

实现的方法是从下到上逐步更新 Splay。
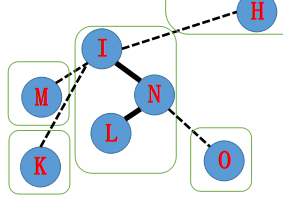
首先我们要把\(N\)旋至当前Splay的根。
为了保证辅助树的性质，原来\(N\)到\(O\)的实边要更改为虚边。
由于认父不认子的性质，我们可以单方面的把\(N\)的儿子改为\(Null\)。
于是原来的辅助树就从下图变成了下下图。

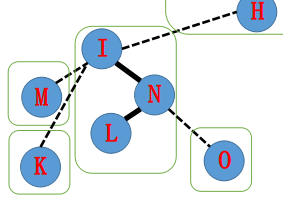
下一步，我们把 \(N\)指向的 Father \(I\) 也旋转到 \(I\) 的 Splay 树根。
原来的实边\(I-K\) 要去掉，这时候我们把\(I\)的右儿子指向\(N\),
就得到了 \(I-L\) 这样的Splay。

接下来，按照刚刚的操作步骤，由于 \(I\) 的 Father 指向 \(H\), 我们把 \(H\) 旋转到他所在 Splay 的根，然后把 \(H\) 的右儿子设为\(I\) 。

之后的树是这样的。

同理我们 \(Splay(A)\), 并把 \(A\) 的右儿子指向 \(H\) 。
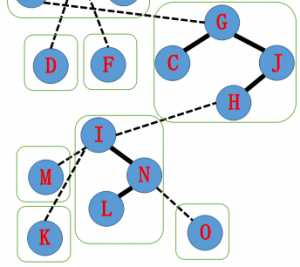
于是我们得到了这样一棵辅助树。并且发现\(A\)—\(N\)的整个路径已经在同一棵 Splay 中了。

以上摘自oiwiki
最后我们看下代码

int access(int x){
    int p=0;
    for(;x;p=x,x=f[x]){
        splay(x);ch[x][1]=p;pushup(x);
    }return p;
}

最后返回的值是x所在splay的根，
值得一提的是连续两次access返回的是两个点lca。

下传标记：

void update(int x){if(!isrt(x))update(f[x]);pushdown(x);}

我们现在要实现一个操作：使一个点成为原树的根，
考虑如何实现这种操作。
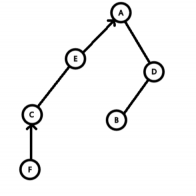
将树用有向图表示出来，儿子到父亲有一条边，
换根相当于将x到根的路径的所有边方向取反，
而在splay中就是一个子树翻转。
先access(p)，把p到根的路径变为一条实路径，然后splay(p)使它成为根，然后打标记。

void mkrt(int x){access(x);splay(x);pushrev(x);}

找x所在辅助树的根。先access(x)再splay(x)然后根就是最小的点。
记得下传标记，否则左右儿子搞反会走错节点。

int find(int x){
    access(x);splay(x);pushdown(x); 
    while(ch[x][0])pushdown(x=ch[x][0]);
    splay(x);return x;
}

连边。先判是否连通，然后直接连。认父不认子。

void link(int x,int y){
    if(find(x)!=find(y)){mkrt(x);f[x]=y;}
}

如何取出\(x\)到\(y\)的路径?做完后y是splay的根.

void split(int x,int y){mkrt(x);access(y);splay(y);}

先判连通性，再取出路径，然后判一下是否连通，find比较慢，所以用if

void cut(int x,int y){
    split(x,y);
    if(ch[y][0]==x&&!ch[x][1])
        ch[y][0]=f[x]=0;
    pushup(x);
}

注意事项

1.pushdown和pushup不要漏。
2.pushup里要判空和清空\(0\)节点，不要会有奇怪的事情发生，
真实故事：没清0改某题用了3小时。
3.splay里要判根。

然后上面一道例题也很简单，split(x,y)，输出siz[y]-1即可。

练习：

简单题

BZOJ3282Tree
异或和直接维护就行了，单点改值直接改，改完后pushup
luogu动态树模板
和上题一样
[HNOI2010]弹飞绵羊
建个虚点，套用例题解法即可。
Tree II
维护乘标记和加标记。
[SDOI2011]染色
维护颜色段数，树剖经典题，用lct又短又快。
[SHOI2014]三叉神经树
我们维护1儿子的个数\(A_i\)，修改很显然是一段叶子结点\(x\)到根节点路径的一段后缀。
以0改成1为例，那么就是向上连续一段\(A_i\)都为\(1\)的。
那么1改成0就是连续一段\(A_i\)都为\(2\)的。
这个可以二分。但是我们是可以直接在splay上维护的。
我们只需要维护深度最深的那个\(A_i\)不为\(1\)或\(2\)的点即可。
[SDOI2008] 洞穴勘测
判连通。使用find
luogu3950部落冲突
和上题一样

维护边双连通分量

使用并查集维护。

[AHOI2005] 航线规划
众所周知必经边就是两点间边双的个数+1。
如果把每个边双看成一个点，那么答案就是split(x,y)后的siz[y]-1.
删边并不好做，我们离线下来从后往前加边做。
如果没连通直接连，否则就把\(x\)到\(y\)缩成一个点。
我们用并查集来实现缩点。
我们暴力把\(x\)到\(y\)路径上的所有点的\(fa_x\)一个一个的改成一个代表点。然后删除这些点。
因为每个点只会被删一次，所以均摊仍是\(O(nlogn)\)的。
BZOJ2959长跑
和上题一样，多维护一个子树和。

维护边权

lct没有固定的父子关系，不能像树剖一样直接记在某个点上。
我们把边转成点即可。加边删边都是两次。

最小差值生成树
差值最小，那么最大值固定时，最小值要最大。
按边权排序，然后从小到大加边。然后用一个指针指向未被删除的最小边。
每次加边查询是否连通，没连通直接加，
否则查询路径上的边，把它删了，打个删除标记，然后加上当前边。
用当前边减去最小边更新答案。
WC[2006]水管局长
同样离线后倒着做，显然答案是最小生成树上两点之间边权的最小值。
动态维护最小生成树。
NOI[2014]魔法森林
按\(A_i\)排序，对于\(B_i\)维护一个最小生成树。

维护子树信息

LCT不能很方便的进行子树统计，需要进行一点修改。

BJOI[2014]大融合
答案很显然是断开\((x,y)\)这条边后两棵树大小的乘积。
考虑如何在splay上维护子树大小。
我们设\(siz_x\)为x所在Splay以x为根的子树大小，
设\(sz_x\)为\(x\)所有虚儿子的子树大小。
那么显然\(siz_x=sz_x+siz_{ls}+siz_{rs}+1\)
在access时会改变右儿子，此时就要修改一下，如下：

void access(int x){
    int p=0;
    for(;x;p=x,x=f[x]){
        splay(x);
        sz[x]+=siz[ch[x][1]]-siz[p];//加上修改时的差量
        ch[x][1]=p;pushup(x);
    }
}

而link的时候同样要修改

void link(int x,int y){
    mkrt(x);mkrt(y);
    f[x]=y;sz[y]+=siz[x];
    pushup(y);
}

cut并不需要，因为只是删去一条实边。
上述方法只能维护有区间可减性的信息。
例如最值则不可以，但最值可以用另一种方法维护。
就是为每个节点开一个\(set\)即可。

luogu首都

动态维护树的重心。
当合并两个树时，可以用启发式合并。
将大小较小的那棵树的所有节点link到另一棵树上，
每次重心最多移动一个位置，我们每次检查当前重心子树大小是否超过树大小一半修改即可。
时间复杂度\(O(nlog^2n)\)，但这并不是最优秀的做法。
有一个性质，两棵树合并后的新重心在原来两个旧重心的路径上。
我们把这个路径split出来。然后在splay遍历一条链实现一个二分的过程。
具体实现就是对于每个splay节点的左右儿子，选择大小较大的那一边，
当遇到一个节点的左右两边树的大小都不大于新树大小一半就是重心。
对于大小为偶数的树可能有两个重心，取编号较小的那个。时间复杂度\(O(nlogn)\)

学有余力项目

《学有余力》的同学可以完成下列题目：
Sone1(Top Tree模板，可魔改LCT，动态树全家桶)
Qtree系列7题(不难但适合练手)
[ZJOI2018]历史(毒瘤)
[ZJOI2016]大森林(毒瘤)

posted @ 2021-08-09 18:26 Isenthalpic 阅读(108) 评论(2) 编辑收藏举报

刷新页面返回顶部

Isenthalpic