[知识学习] 主席树
这两天学习了主席树，基本上搞懂了主席树是怎么操作的
主席树，是一种可持久化线段树。最简单的操作就是维护静态区间第 \(k\) 小
主席树通过维护历史版本，实现查询区间的有关操作
主席树的原理
假设现在有这么一个序列：\(4, 1, 3, 5, 2\)
问如何求出区间 \([1,3]\) 内大小为第二的数？
利用大眼观察法，很显然是3
那么让计算机去怎么实现呢？它又没有眼睛
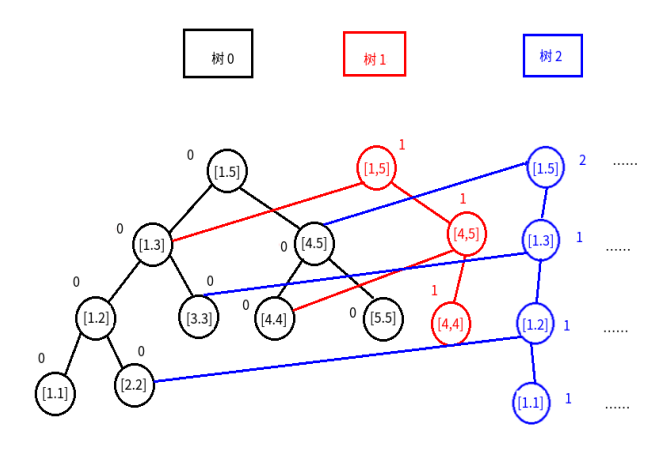
对于这个序列，我们可以先建一颗空的权值线段树，命名为“树 \(0\) ”（方便后面的使用），如图：
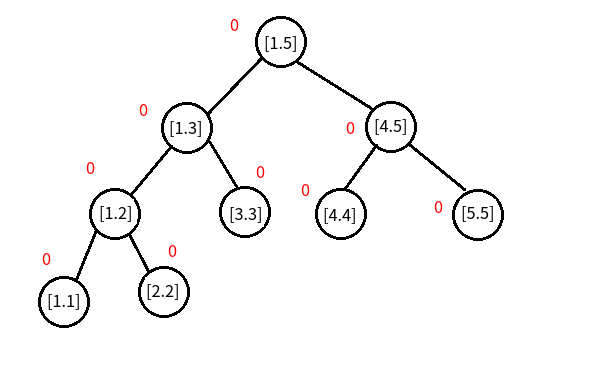
别告诉我你不知道什么是权值线段树，自己去百度；
现在序列里面第一个数是 \(4\)，我们往树里面插入一个 \(4\) ，因为要保留历史版本，所以我们对 \(4\) 这个数新建一颗线段树，命名为“树 \(1\) ”，如图：
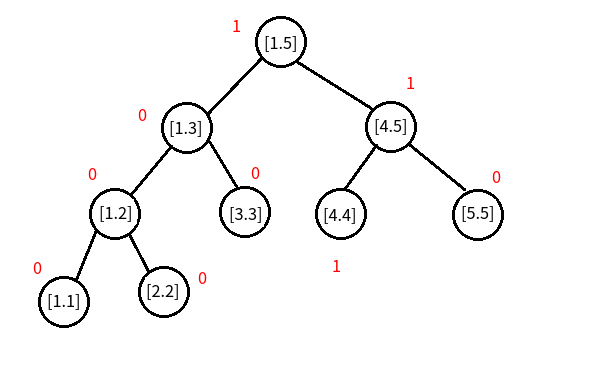
为什么是这样呢？
\(1\le 4 \le5\)，故区间 \([1,5]++\);
\(4\le 4 \le5\)，故区间 \([4,5]++\);
\(4\le 4 \le4\)，故区间 \([4,4]++\);
其他的还是 \(0\) ;
懂了没有。。。
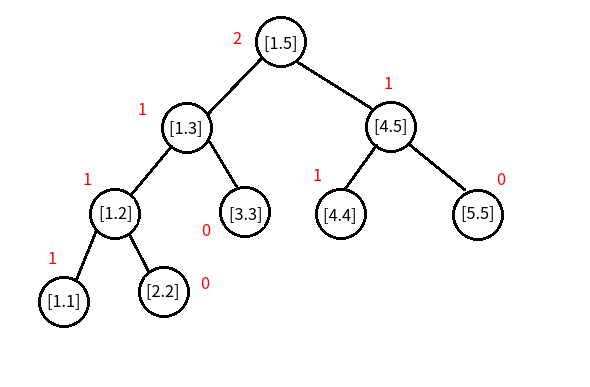
继续插入第二个数 \(1\) ，建成“树 \(2\) ” ，这里不解释了
再插入第三个数 \(3\)，建成“树 \(3\) ”
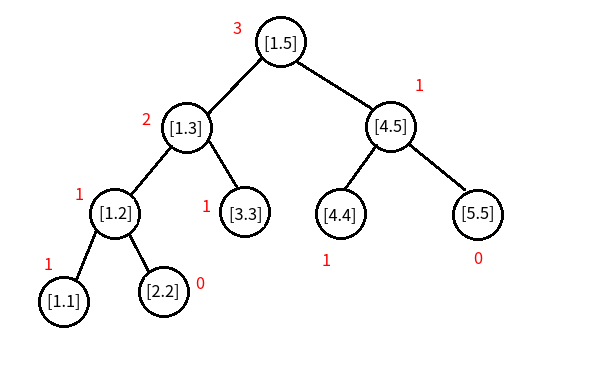
OK！现在我们就已经可以求出 \([1,3]\) 内的大小为第二大的数了
递归操作查询排名应该都会吧？
不会的看这里：
-
进入 \([1,5]\) 节点，我们发现他的左儿子的子树个数为\(2\) ， $2\le k $ \((k=2)\)，于是进入\([1,3]\)节点;
-
然后我们发现 \([1,3]\) 节点的左儿子子树个数\(1 < k\) \((k=2)\)，于是进入 \([3,3]\) 节点；
-
此时我们把 \(k\) 更新为 \(1\) (\(2-1=1\));
-
走到头了，于是就返回 \(3\) ，所以答案就是 \(3\) ，也就是原来的序列区间 \([1,3]\) 的第 \(2\) 小就是 \(3\)
现在你明白了主席树是怎么操作了的吧？
疑问
但是有一个问题：上面我们求的是区间\([1,r]\)的第 \(k\) 大的数
同理，区间 \([1,r]\) (\(r\in\) \([1,n]\) , \(r \in N\))的第 \(k\) 大数我们也就会求了
那怎么求区间 \([l,r]\) 的第 \(k\) 大数呢？
举个例子，求区间\([2,3]\)的第 \(k\) 大数
我们拿建出来的“树 \(3\) ”减掉“树 \(1\) ”后，再进行如上操作就可以了
这也就是前缀和思想
所以对于区间\([l,r]\) 我们拿“树 \(r\) ”减去“树 \((l-1)\) ”，再query一下就可以求得答案了
还有一个问题：我每个数都开一个线段树来存，空间不会炸掉吗？
所以主席树是这样操作的：
- 每插入一个数 \(x\) ，只有 \([x,x]\) 到 \([1,n]\) 一条链上的点会更新操作，所以我们可以共用一些点，就OK了，如图：
例题与代码
那么主席树就介绍完了，具体实现给个例题让大家看看，还有不懂得可以再参考一下他人的博客
#include <bits/stdc++.h>
#define N (200000+5)
#define ls ch[rt][0]
#define rs ch[rt][1]
#define vl ch[vs][0]
#define vr ch[vs][1]
using namespace std;
int n,m,q;
int rt[N],ch[N<<5][2],tot,val[N<<5];//rt:每个线段树的根，ch：左右儿子，tot：编号总数，val：权值
int a[N],b[N];//a：原数组，b：离散化数组
inline int query(int x){//离散化
return lower_bound(b+1,b+m+1,x)-b;//离散化
}
inline void update(int &rt,int vs,int l,int r,int k){//更新，新建一棵树
rt=++tot;//新树的根节点为tot++
ls=vl,rs=vr;//左右儿子都是历史版本的左右儿子
val[rt]=val[vs]+1;//新加入一个数，rt的权值++
if(l==r) return;//叶子节点，return
int mid=(l+r)>>1;//mid为分割区间的中点
if(k<=mid) update(ls,vl,l,mid,k);//k<=mid，k在左儿子
else update(rs,vr,mid+1,r,k);//否则k在右儿子
}
inline int query(int rt,int vs,int l,int r,int k){//询问第k大
if(l==r) return l;//找到了（在叶子节点），return
int mid=(l+r)>>1;
int v=val[vl]-val[ls];
//这里只用算一下k在不在左儿子就行了，不再左儿子就肯定在右儿子
//这里用当前版本减去历史版本就是类似“前缀和”操作
if(k<=v) return query(ls,vl,l,mid,k);//在左儿子，继续找
else return query(rs,vr,mid+1,r,k-v);//不在左儿子，找右儿子，并把k减去左边所有的个数
}
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[i]=a[i];//读入
sort(b+1,b+n+1);//离散化数组先排序
m=unique(b+1,b+n+1)-b-1;//离散化
for(int i=1;i<=n;i++){
update(rt[i],rt[i-1],1,n,query(a[i]));
//一个节点一个节点的插入；
//这里对rt进行引用（&），相当于rt[i]=update(rt[i],rt[i-1],1,n,query(a[i]));
}
while(q--){
int l,r,k;
scanf("%d%d%d",&l,&r,&k);
printf("%d\n",b[query(rt[l-1],rt[r],1,n,k)]);//求解静态区间第k小，注意是l-1和r
}
return 0;
}
