[2019 CSP-S赛前集训] [P3959] [蒟蒻Xx_queue学DP] 3.宝藏
蒟蒻Xx_queue又来更博客啦!!!
话说之前一直都没有讲到与状压DP枚举子集有关的知识,那我们今天就来补充一下;
今天要讲的题目是:
[NOIP2017TG] 宝藏
题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了\(n\)个深埋在地下的宝藏屋, 也给出了这\(n\)个宝藏屋之间可供开发的\(m\)条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏屋之间的道路无需再开发。
新开发一条道路的代价是:
\(\mathrm{L} \times \mathrm{K}\)
\(L\)代表这条道路的长度,\(K\)代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
输入格式
第一行两个用空格分离的正整数 \(n\),\(m\),代表宝藏屋的个数和道路数。
接下来 \(m\) 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 \(1 - n\)),和这条道路的长度 \(v\)。
输出格式
一个正整数,表示最小的总代价。
输入输出样例
输入 1
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出 1
4
输入 2
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2
输出 2
5
说明/提示
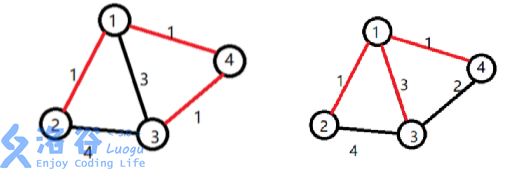
【样例解释1】
小明选定让赞助商打通了\(1\) 号宝藏屋。小明开发了道路 \(1 \to 2\),挖掘了 \(2\) 号宝 藏。开发了道路 \(1 \to 4\),挖掘了 \(4\) 号宝藏。还开发了道路 \(4 \to 3\),挖掘了\(3\)号宝 藏。工程总代价为:\(1 \times 1 + 1 \times 1 + 1 \times 2 = 4\)
【样例解释2】
小明选定让赞助商打通了\(1\) 号宝藏屋。小明开发了道路 \(1 \to 2\),挖掘了 \(2\) 号宝 藏。开发了道路 \(1 \to 3\),挖掘了 \(3\) 号宝藏。还开发了道路 \(1 \to 4\),挖掘了\(4\)号宝 藏。工程总代价为:\(1 \times 1 + 3 \times 1 + 1 \times 1 = 5\)
【数据规模与约定】
对于20%的数据: 保证输入是一棵树\(1≤n≤8\),\(v≤5000\) 且所有的 \(v\)都相等。
对于 40%的数据: \(1≤n≤8\),\(0≤m≤1000\),\(v≤5000\) 且所有的\(v\)都相等。
对于70%的数据: \(1≤n≤8\),\(0≤m≤1000\),\(v≤5000\)
对于100%的数据: \(1≤n≤12\),\(0≤m≤1000\),\(v≤500000\)
分析:
先看数据范围:\(1≤n≤12\),不是爆搜就是状压DP;(爆搜加玄学剪枝当然可以过,详解见洛谷题解)
(玄学的模拟退火就算了,不知道你们有没有想到最小生成树,然而是行不通的)
这里我就来讲一讲状压DP的做法,毕竟前面我才刚刚写了一个状压DP的学习总结嘛(这回不是玉米田了);
因为题目中说到:新开发一条道路的代价是:
\(\mathrm{L} \times \mathrm{K}\)
\(L\)代表这条道路的长度,\(K\)代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋。
所以这个题目应该和你打通的数的层数有关系(因为你需要计算K啊);
所以不妨设\(f_{i,j}\)表示已经打通的宝藏屋中的最大深度为\(i\),宝藏屋打通的状态(状压,二进制,大概明白是什么意思吧?)为\(j\),
\(j\)的每一位中1代表这个宝藏屋已经打通了,0表示没有打通;
现有的状态可以由 这个状态的子集+新打通的一些宝藏屋 转移过来
所以比较容易得出状态转移方程就是\(f_{i,j}=min\{f_{i-1,k}+(i-1)*c_{k,j}\}\)
其中\(i\)为深度,\(j\)为目标状态,\(k\)为\(j\)的子集,\(c_{k,j}\)代表从状态\(k\)转移至\(j\)的花费(也就是把集合\(j\)的子集\(k\)添加一部分元素变成集合\(j\)所需要的代价)
蒯了一个图,大家看一看:(来自洛谷题解)
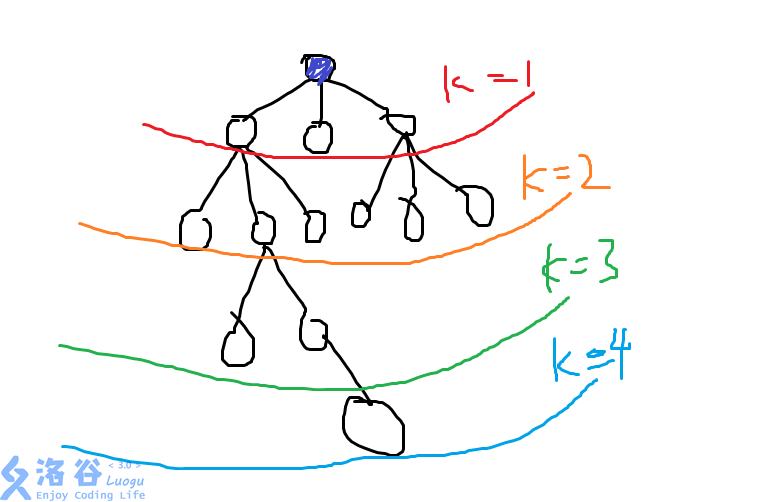
大概就是这样吧,不知道你搞懂了吗??
这里注意一些细节:我们需要预处理出从状态\(k\)转移至\(j\)的花费(下面的代码中用trans数组储存),还要记得开long long!
具体细节以及实现过程请研究代码:
AC代码:
#include <bits/stdc++.h>
#define N 13
#define INF 0x3f3f3f3f
using namespace std;
int n,m;
int dis[N][N];//两个宝藏屋之间的距离
int trans[1<<N][1<<N];//从一个状态转移至另一个状态(从集合的子集转移至该集合)的花费
long long dp[N][1<<N];//dp[i][j],i表示深度,j表示状态(二进制数)
void gettrans(){//取得转移花费
int siz=(1<<n);
for(int i=0;i<siz;i++){
for(int j=i;j!=0;j=(j-1)&i){//枚举i的子集
bool rightt=true;
int now=i^j;//now为i-j(集合相减),得到的是j中不含而i中含有的元素
for(int k=n;k>=1;k--){//枚举集合now的每一位
if(now>=(1<<(k-1))){//now的第k位是否为1
int minn=INF;
for(int l=1;l<=n;l++)
if(((1<<(l-1))&j)==(1<<(l-1))) minn=min(minn,dis[l][k]);//求出转移花费
if(minn==INF){
rightt=false;
break;
}
trans[j][i]+=minn;
now-=(1<<(k-1));//继续求
}
}
if(rightt==false) trans[j][i]=INF;//转移不了视为inf
}
}
}
void DP(){//dp
int siz=(1<<n);
memset(dp,0x3f,sizeof(dp));//初始化为inf
for(int i=1;i<=n;i++){
dp[1][1<<(i-1)]=0;//只有一层,则为0(免费开采第一层)
}
for(int i=2;i<=n;i++){
for(int j=0;j<siz;j++){
for(int k=j;k!=0;k=(k-1)&j){//枚举子集
if(trans[k][j]!=INF) dp[i][j]=min(dp[i][j],dp[i-1][k]+trans[k][j]*(i-1));//转移方程(前面详细讲过了,不知道的回炉重造)
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
memset(dis,0x3f,sizeof(dis));
for(int i=1;i<=m;i++){//读入不用解释
int u,v,wei;
scanf("%d%d%d",&u,&v,&wei);
if(wei<dis[u][v]){
dis[u][v]=dis[v][u]=wei;
}
}
gettrans();
DP();
long long ans=0x3f3f3f3f3f3f3f3f;
int siz=(1<<n);
for(int i=1;i<=n;i++) ans=min(ans,dp[i][siz-1]);//统计答案
printf("%lld",ans);
return 0;
}
怎么样?除了玉米田,可见枚举子集也是非常非常重要的(当然还有集合的基本运算),相信你弄懂这道题目后对于状压DP有更加理解了;
还是要多多练习啊!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号