串的模式匹配算法
串的模式匹配算法
BF(Brute-Force)算法
模式匹配不一定是从主串的第一个位置开始,可以指定主串中查找的起始位置pos。如果采用字符串顺序存储结构,可以写出不依赖于其他串操作的匹配算法。
算法步骤
-
分别利用计数指针\(i\)和\(j\)指示主串\(S\)和模式串\(T\)中当前正待比较的字符位置,\(i\)初值为 pos,\(j\)初值为 1。
-
如果两个串均未到串尾,即\(i\)小于等于\(S\)的长度且\(j\)小于等于\(T\)的长度时,则循环执行以下操作:
-
\(S[i]\)和\(T[j]\)比较,若相等,则\(i\)和\(j\)分别指示串中下个位置,继续比较后序字符;
-
若不等,指针后退重新开始匹配,从主串的下一个字符\((i=i-j+2)\)起重新和模式串的第一个字符\((j=1)\)比较。
-
-
如果\(j\)大于\(T\)的长度,说明模式串\(T\)中的每个字符依次和主串\(S\)中的一个连续的字符序列相等,则匹配成功,返回和模式串\(T\)中第一个字符相等的字符在主串\(S\)中的序号\((i-T的长度)\);否则称匹配不成功,返回0。
下面的一系列图展示了模式串\(T="abcac"\)和主串\(S\)的匹配过程(pos = 1)。
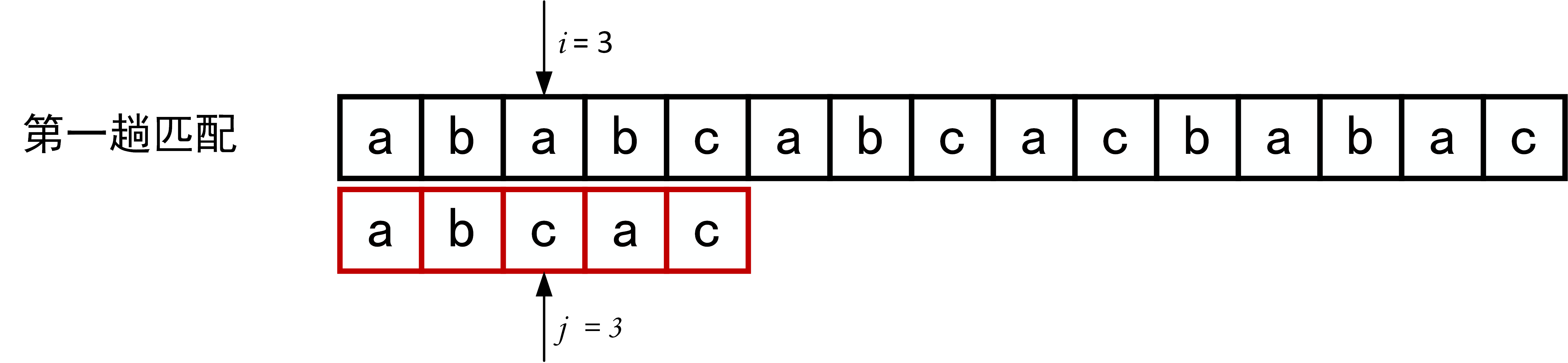
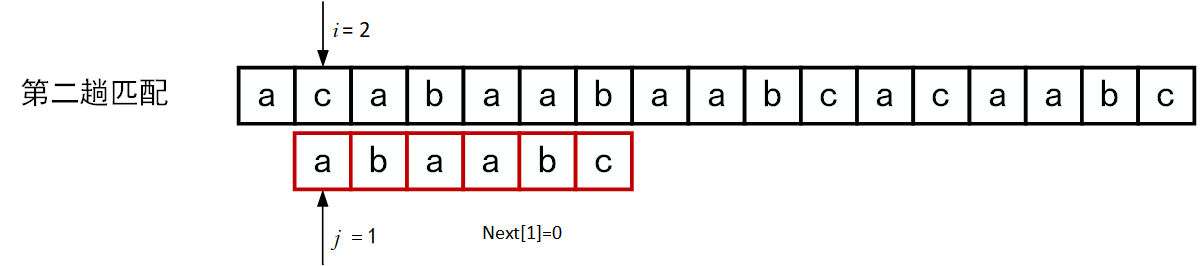
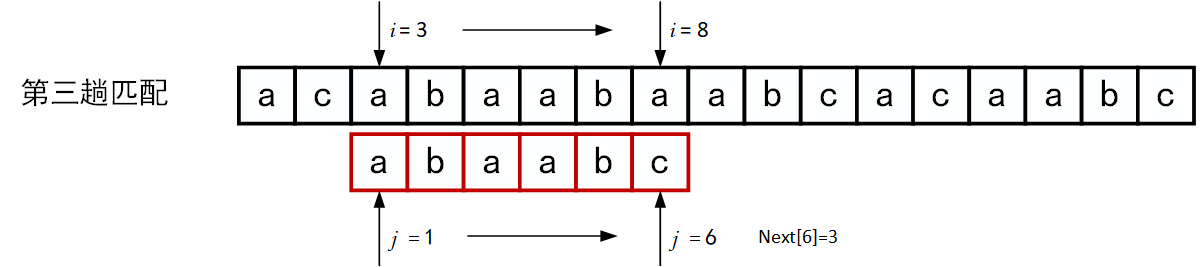
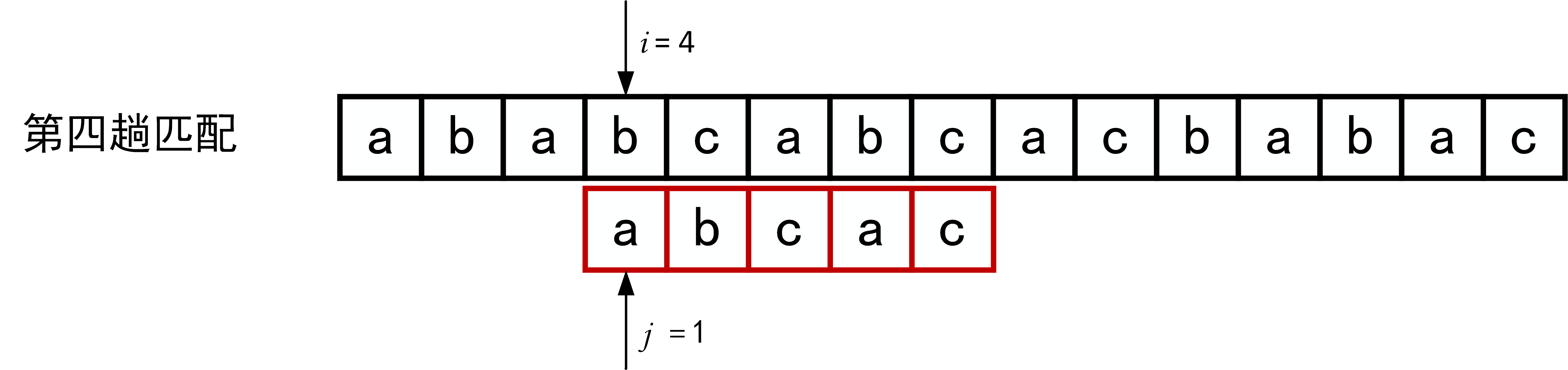
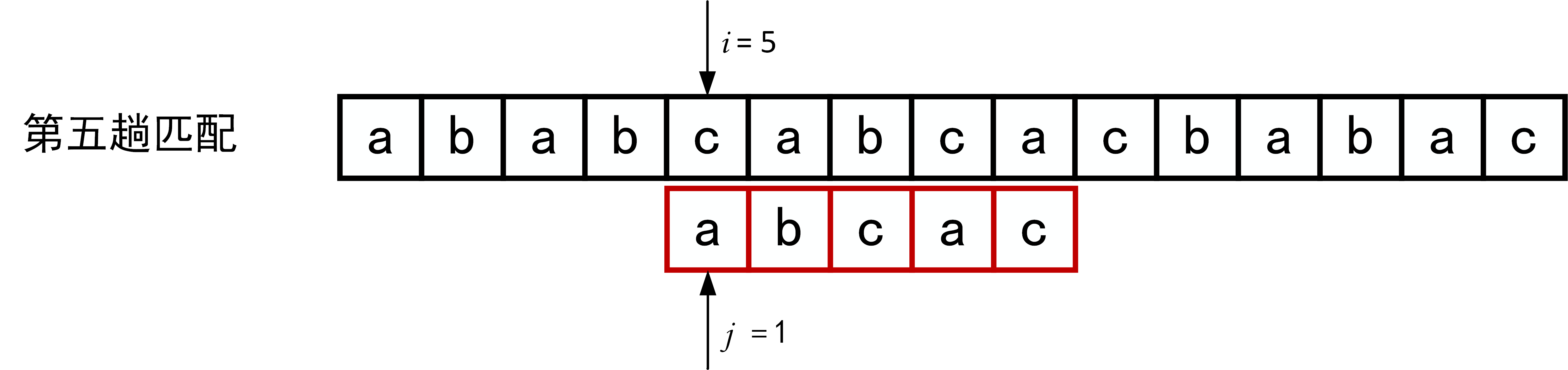
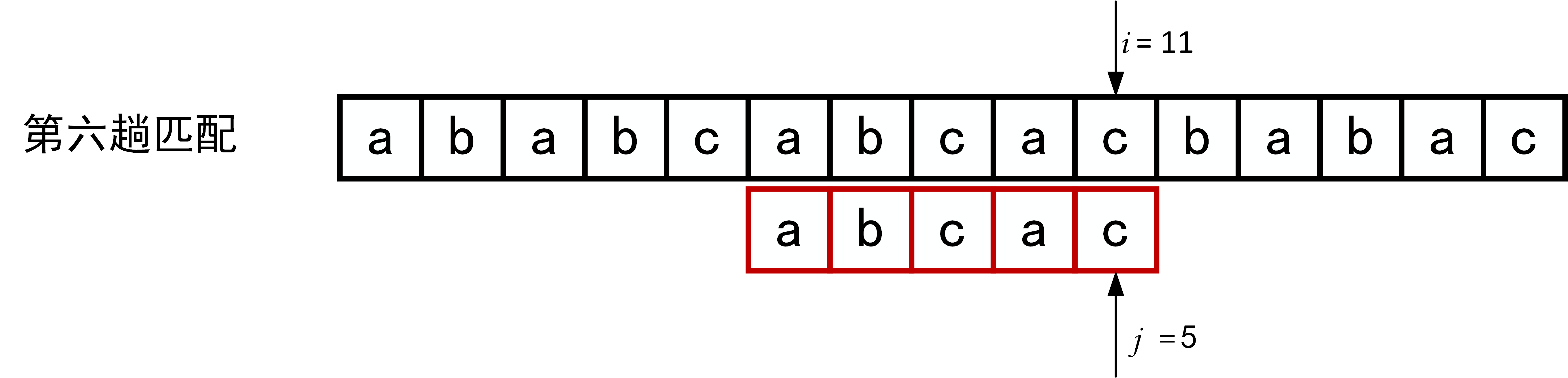
算法实现
int StrIndex_BF(SString S,SString T,int pos)
{
int i,j;
if(pos <= 1 && pos <=S[0]){
i = pos;
j = 1;
while(i <= S[0] && j <= T[0]){
if(S[i] == T[j]){
i++;
j++;
}
else{
i = i - j + 2;
j = 1;
}
}
if(j > T[0])
return i - T[0];
else
return 0;
}
else{
return 0;
}
}
KMP算法
定义
该算法是由Knuth、Morris和Pratt同时设计实现的,因此简称KMP算法。其相较于BF算法,改进在于:每当一趟匹配过程中出现字符比较不相等时,不需要回溯i指针,而是利用已经得到的“部分匹配”的结果将模式串向右“滑动”尽可能远的一段距离后,继续进行比较。
核心思想
移动模式串,使模式串中的公共前后缀里面的前缀移动到后缀的位置。
举例说明
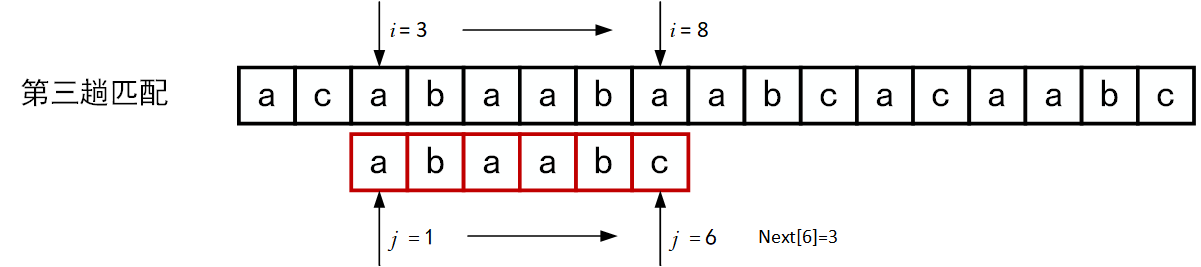
回顾BF匹配算法的过程示例,在第三趟的匹配中,当\(i=7、j=5\)字符比较不等时,又从\(i=4、j=1\)重新开始比较。然后,经自习观察可以发现,\(i=4\)和\(j=1\),\(i=5\)和\(j=1\),以及 \(i=6\)和\(j=1\)这三次比较都是不必进行的。因为从第三趟部分匹配的结果就可以得出,主串中第4个、第5个和第6个字符必然是“b”、“c”和“a”(也就是模式串中的第2个、第3个和第4个字符)。因为模式串中的第一个字符是“a”,因此它无需再和这3个字符进行比较,而仅需将模式串向右滑动3个字符的位置继续进行\(i=7、j=2\)时的字符不比较即可。同理,在第一趟匹配中出现字符不等时,仅需将模式串向右移动两个字符的位置继续进行\(i=3、j=1\)时的字符比较。由此,在整个匹配的过程中,\(i\)指针没有回溯,如下图所示。
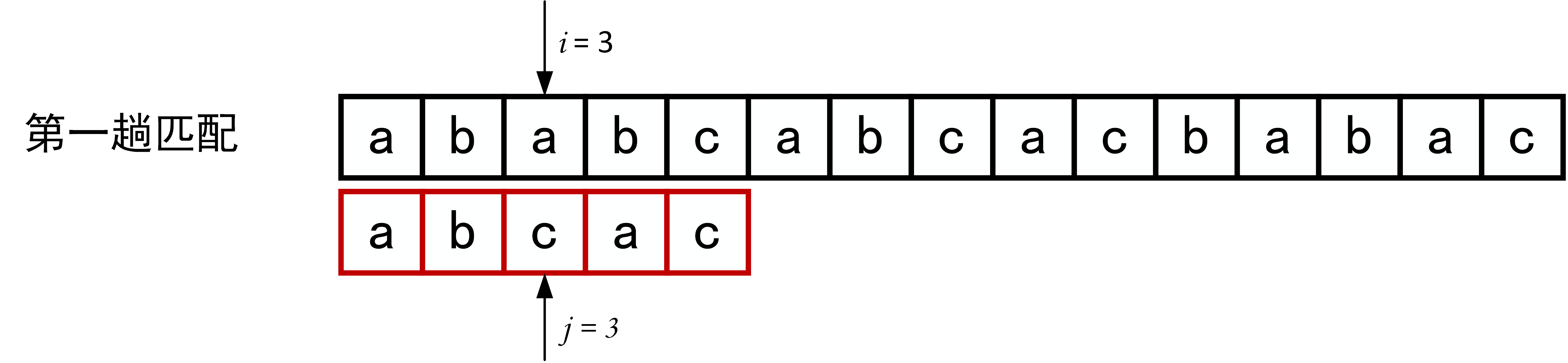
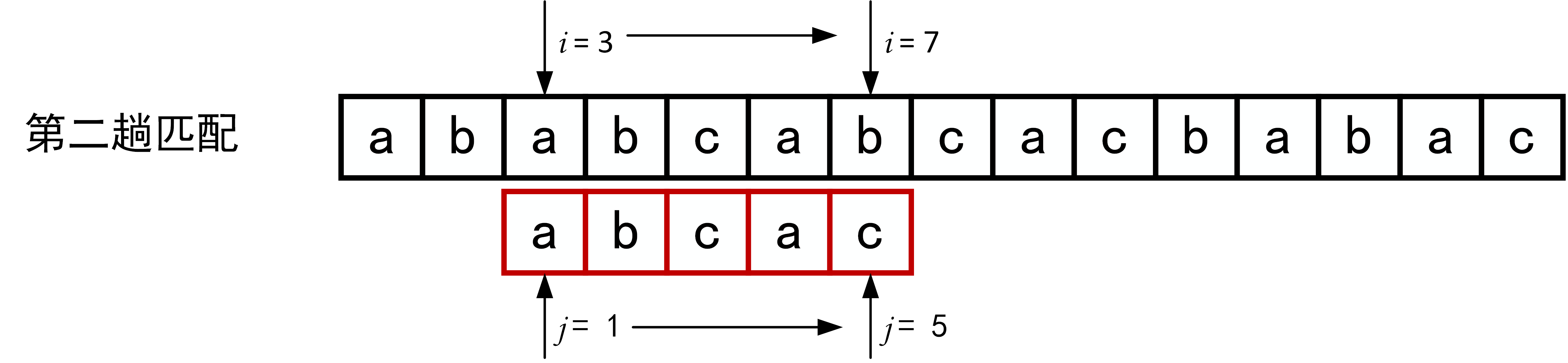
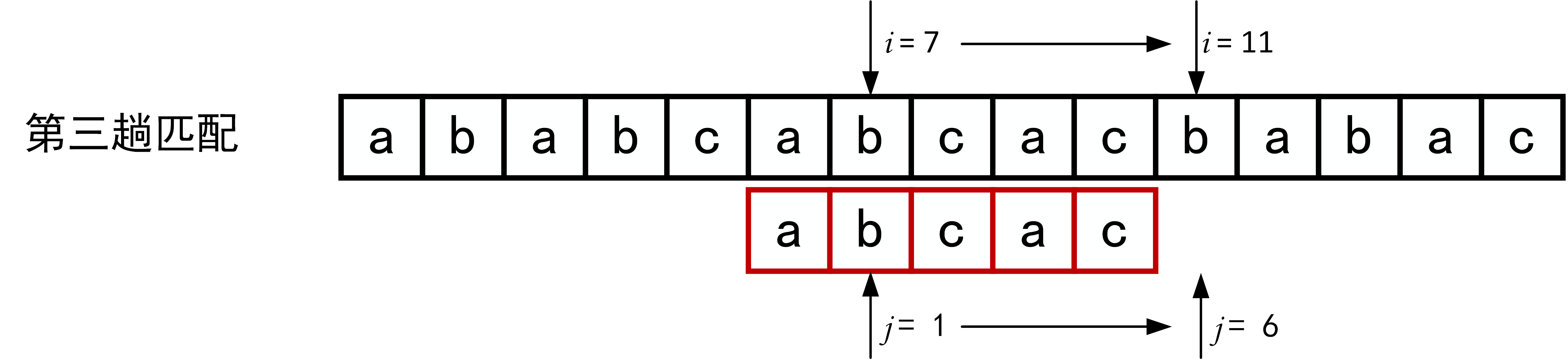
现在再来讨论一般情况。假设主串为\("s_1s_2s_3\ldots s_n"\),模式串为\("t_1t_2t_3\ldots t_m"\),从上面的分析可以知道,为了实现改进算法,需要解决下述问题:当匹配过程中产生“失配”(即\(s_i\neq t_j\))时,模式串“向右滑动”可行的距离多远,换句话说,当主串中第\(i\)个字符与模式串中第\(j\)个字符“失配”(即比较不等)时,主串中第$ i \(个字符(\)i$指针不回溯)应与模式串中哪个字符再比较。
假设此时应与模式串中第\(k\)(\(k<j\))个字符继续比较,则模式串中前\(k-1\)个字符的子串必须满足下列关系式,且不可能存在\(k^ ,>k\)满足下列关系式:
$$ "t_1t_2t_3\ldots t_{k-1}"="s_{i-k+1}s_{i-k+2}\ldots s_{i-1}"\quad\quad\quad\quad\quad(1)$$
而已经得到的"部分匹配"的结果是:
$$ "t_{j-k+1}t_{j-k+2}\ldots t_{j-1}"="s_{i-k+1}s_{i-k+2}\ldots s_{i-1}"\quad\quad\quad\quad\quad(2) $$
由上面两个式子可以推得下列等式:
$$ "t_1t_2\ldots t_{k-1}"="t_{j-k+1}t_{j-k+2}\ldots t_{j-1}" \quad\quad\quad\quad\quad (3) $$
反之,若模式 串中存在满足式(3)的两个子串,则当匹配过程中,主串中第\(i\)个字符与模式串中第\(j\)个字符比较不等时,仅需将模式串向右滑动至模式串中第\(k\)个字符和主串中第\(i\)个字符对齐,此时,模式串中头\(k-1\)个字符的子串\(t_1t_2\ldots t_{k-1}\)必定与主串中第\(i\)个字符之前长度为\(k-1\)的子串\(“s_{i-k+1}s_{i-k+2}\ldots s_{i-1}”\)相等,由此,匹配仅需从模式串中第\(k\)个字符与主串中第\(i\)个字符开始,依次向后进行比较。
视频学习地址:KMP算法通俗易懂视频
实现
若令\(next[j]=k\),则\(next[j]\)表明当模式串中第\(j\)个字符与主串中相应字符“失配”时,在模式串中需重新和主串中该字符进行比较的字符的位置。
next函数
- 从头开始的\(k-1\)个元素就是字符串的前缀
- \(j\)前面的\(k-1\)个元素就是字符串的后缀
举例如下:
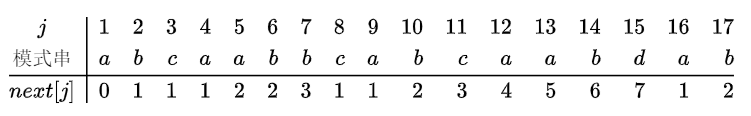
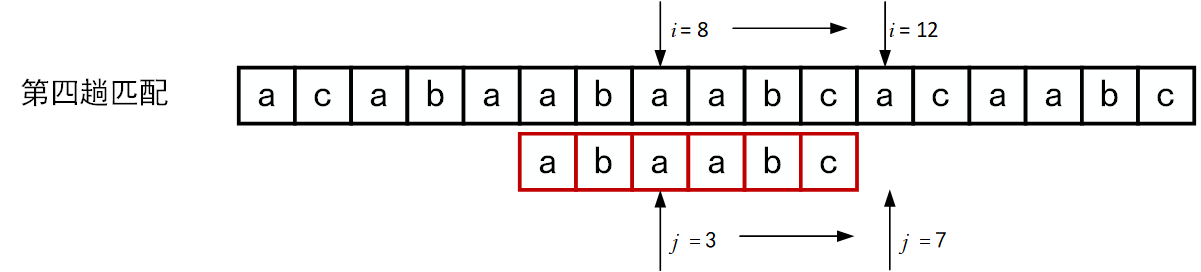
在求得模式串的\(next\)函数之后,匹配可如下进行:假设以指针\(i\)和\(j\)分别指示主串和模式串中正待比较的字符,令\(i\)的初值为pos,\(j\)的初值为1。若在匹配过程中\(S_i=T_j\),则\(i\)和\(j\)分别增1,否则,\(i\)不变,而\(j\)退到\(next[j]\)的位置再比较,若相等,则指针各自增1,否则\(j\)再退到下一个\(next\)值得位置,依次类推,直至下列两种可能:一种是\(j\)退到某个\(next\)值\((next[next[...next[j]...]])\)时字符比较相等,则指针各自增1,继续进行匹配;另一种是\(j\)退到值为零(即模式串的第一个字符失配),则此时需将模式串继续向右滑动一个位置,即从主串的下一个字符\(S_{i+1}\)起和模式串重新开始匹配。下图所示正是这段话匹配过程的一个例子。
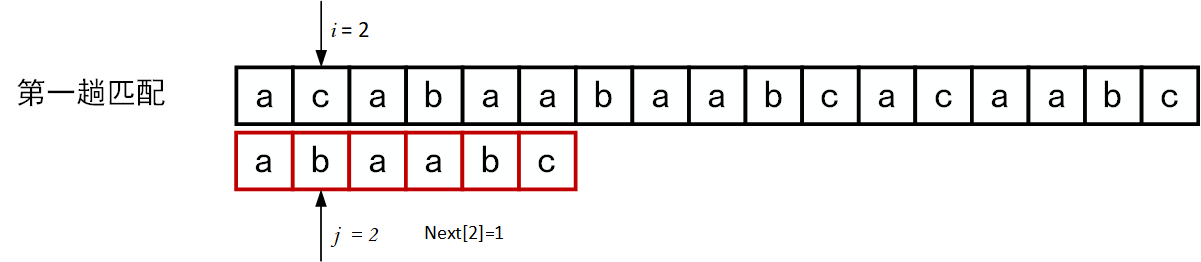
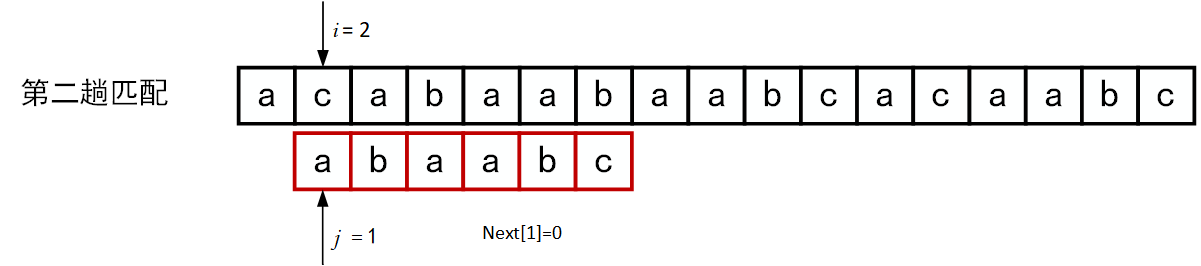
算法实现
//KMP算法实现过程
int StrIndex_KMP(SString S,SString T,int pos)
{
int i,j;
if(1 <= pos && pos <= S[0]){
i = pos;
j = 1;
while(i <= S[0] && j <= T[0]){
if( j == 0 || S[i] == T[j]){
i++;
j++;
}
else{
j = next[j];
}
}
if(j > T[0])
return i - T[0];
else
return 0;
}
esle{
return 0;
}
}
//next函数求取过程
void Get_Next(SString T,int next[])
{
int i = 1,j = 0;
next[1] = 0;
while(i < T[0]){
if(j == 0 || T[i]==T[j]){//T[i]表示后缀的单个字符,T[j]表示前缀的单个字符
i++;
j++;
next[i] = j;
}
else{
j = next[j];//若字符不相同,则j值回溯至字符相等或者j=0处
}
}
}
next函数背后的原理
- 求\(next[j+1]\),则已知\(next[1]、next[2]\cdots next[j]\);
- 假设\(next[j]=k\),则有\(t_1t_2\cdots t_{k-1}=t_{j-k+1}t_{j-k+2}\cdots t_{j-1}\)(前\(k-1\)位字符与后\(k-1\)位字符重合);
- 如果\(t_k=t_j\),则有\(t_1t_2\cdots t_{k-1}t_k=t_{j-k+1}t_{j-k+2}\cdots t_{j}\),则此时\(next[j+1]=k+1\),否则进入下一步;
- 此时,\(t_k\neq t_j\),假设\(next[k] = k_1\),则有\(t_1\cdots t_{k_1-1}=t_{k-k_1+1}\cdots t_{k-1}\)(前\(k_1-1\)位字符与后\(k_1-1\)位字符重合);
- 第二第三步联合得到:\(t_1\cdots t_{k_1-1}=t_{k-k_1+1}\cdots t_{k-1}=t_{j-k_1+1}\cdots t_{k_1-k+j-1}=t_{j-k_1+1}\cdots t_{j-1}\)
- 这时候,再判断如果\(t_{k_1}=t_j\),则\(t_1\cdots t_{k_1-1t_{k1}=t_{j-k_1+1}\cdots t_{j-1}t_j}\),则\(next[j+1]=k_1+1\);否则再取\(next[k_1]=k_2\)
图解原理
2.求\(next[17]\),已知了\(next[16]\),假设\(next[16]=8\),此时则有\(t_1t_2\cdots t_8=t_9t_{10}\cdots t_{15}\),分两种情况讨论:
- 如果\(t_8=t_{16}\),则非常明显可以看出\(next[17]=8+1=9\)
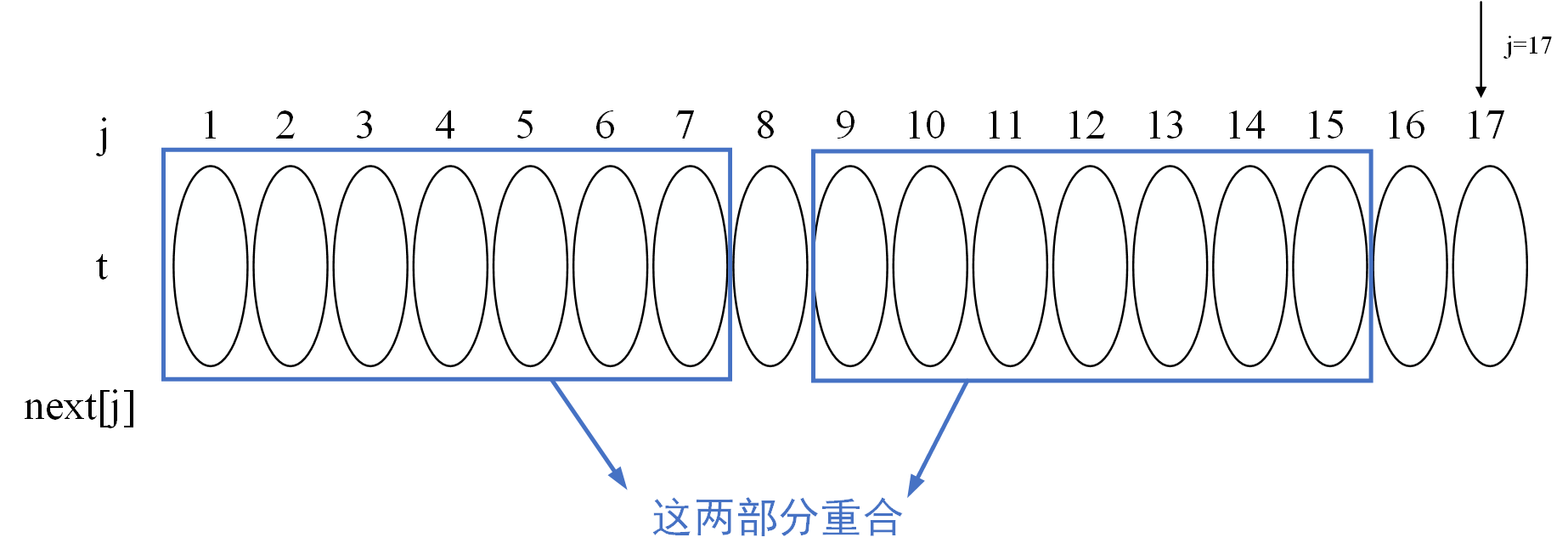
- 如果\(t_8\neq t_{16}\),再假设\(next[8]=4\),则有下图所示的关系:
从而又可以推出下图中所示的四个部分重合,此时需要再进行判断\(t_{16}\text 和t_4\)的关系,同样需要分为两种情况
-
如果\(t_4=t_{16}\),从上图可以看出有:\(t_1\cdots t_4=t_{13}\cdots t_{16}\),则此时\(next[17]=4+1=5\)
-
如果\(t_4\neq t_{16}\),再假设\(next[4]=2\),此时有下图所示的关系:
- 此时,如果\(t_2=t_{16}\),则\(next[17]=2+1=3\)
- 如果\(t_2\neq t_{16}\),\(t_2=1\),\(next[1]=0\),遇到0时还没有结束,则递推结束,此时\(next[17]=1\)
视频学习地址:next函数代码理解视频
算法的改进
前面定义的\(next\)函数在某些情况下尚有缺陷。例如模式串为“aaaab”在和主串“aaaabaaaab”匹配时,当\(i=5、j=5\)时,\(S[5]\neq T[5]\),由\(next[j]\)的指示还需进行\(i=5、j=4,i=5、j=3,i=5、j=2、i=5、j=1\)这四次比较。而实际上,因为模式串中第1~3个字符和第4个字符都相等,因此不需要再和主串中第4个字符相比较,而可以将模式串向右滑动4个字符的位置直接进行\(i=5、j=1\)时的字符比较。这就是说,若按上述定义得到\(next[j]=k\),而模式串中\(t_j=t_k\),则当主串中字符\(S_i\)和\(T_j\)比较不等时,不需要再和\(T_k\)进行比较,而直接和\(T_{next[k]}\)进行比较,换句话说,此时的\(next[j]\)应和\(next[k]\)相同。
//nextval函数求取过程
void Get_Next(SString T,int nextval[])
{
int i = 1,j = 0;
nextval[1] = 0;
while(i < T[0]){
if(j == 0 || T[i]==T[j]){
i++;
j++;
if(T[i] != T[j])
nextval[i] = j;
else
nextval[i] = nextval[j];
}
else{
j = nextval[j];
}
}
}

