树、二叉树、二叉搜索树

一、树

树是一种数据结构，比如：目录结构

树是一种可以递归定义的数据结构，是由n个节点组成的集合

• 如果n=0，那这是一颗空树
• 如果n>0，那存在1个节点作为树的根节点，其它节点可以分为m个集合，每个集合本身又是一棵树

 

二、二叉树

度不超过2的树（节点最多有两个叉）

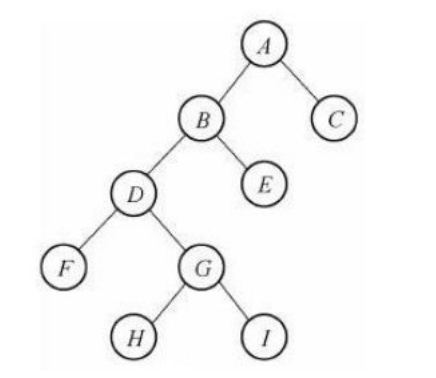
二叉树的链式存储：

将二叉树的节点定义为一个对象，节点之间通过类似链表的链接方式来连接

二叉树的四种遍历方式

1. 前序遍历(根节点在前面)：EACBDGF
2. 中序遍历(根节点在中间)：ABCDEGF
3. 后序遍历(根节点在后面)：BDCAFGE
4. 层次遍历：EAGCFBD

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None

a = BiTreeNode("A")
b = BiTreeNode("B")
c = BiTreeNode("C")
d = BiTreeNode("D")
e = BiTreeNode("E")
f = BiTreeNode("F")
g = BiTreeNode("G")

e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f

root = e
# 前序遍历
def pre_order(root):
    if root:
        print(root.data, end=',')
        pre_order(root.lchild)
        pre_order(root.rchild)

# 中序遍历
def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data, end=',')
        in_order(root.rchild)

# 后序遍历
def post_order(root):
    if root:
        post_order(root.lchild)
        post_order(root.rchild)
        print(root.data, end=',')

# 层级遍历
from collections import deque
def level_order(root):
    que = deque()
    que.append(root)
    while len(que):
        node = que.popleft()
        print(node.data, end=',')
        if node.lchild:
            que.append(node.lchild)
        if node.rchild:
            que.append(node.rchild)

　　

三、二叉搜索树

二叉搜索树是一颗二叉树且满足：设x是二叉树的一个节点，如果y是x左子树的一个节点，那么y.key<=x.key; 如果y是x的右子树的一个节点，那么y.key>=x.key

（左边的都比根节点小，右边的都比根节点大）