冒泡排序、选择排序、插入排序
在开始这三种算法的学习之前,我们要先来补给几个知识:
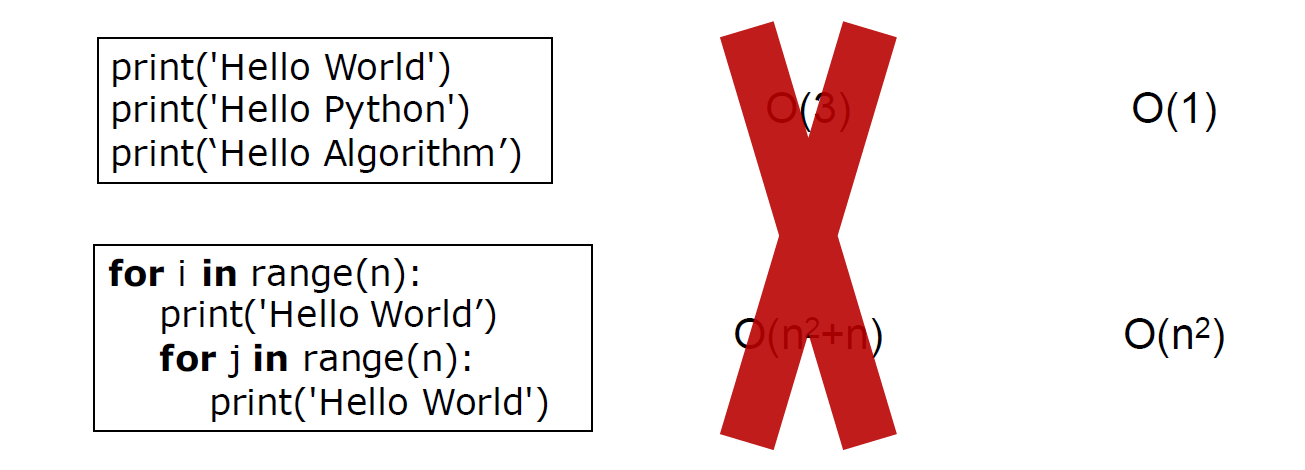
时间复杂度
时间复杂度:用来评估算法运行效率的一个式子


时间复杂度-小结:

快速地判断算法复杂度:
简单情况:
- 确定问题规模n
- 循环减半过程 -- logn
- k层关于n的循环 n的k次方
复杂情况:根据算法执行过程判断
稳定性:
相同值的情况下,排序完两个值的相对位置不会发生变化。
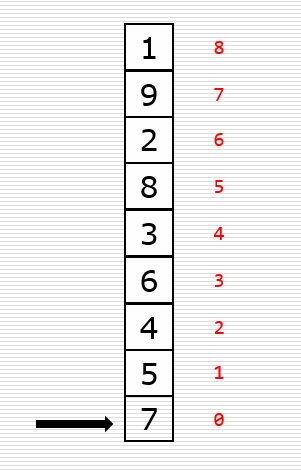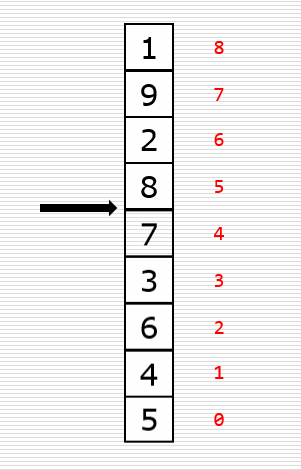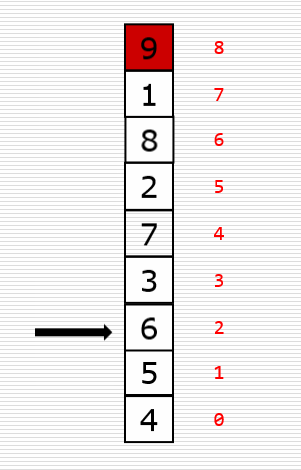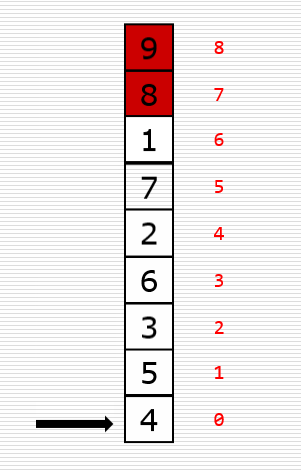
1、冒泡排序(Bubble Sort)
算法描述
比较相邻的两个元素,如果第一个比第二个大,就交换他们两个的位置。(每一趟都会冒出一个有序区的数。)
动图
代码实现
def bubble_sort(li):
# 第一层循环几趟
# len - 1,因为冒泡排序最后一趟的数字已经是最大的了,无需要再走一趟。
for i in range(len(li) - 1):
# 第二层循环,
# - i:在无序区中比较两个数的大小,每一趟结束之后会产生一个有序数字
# - 1:最后一个数字无须遍历,因为在第j次(倒数第二个数字)已经与j+1(倒数第一个数字)次进行了比较
exchange = False
for j in range(len(li) - i - 1):
if li[j+1] < li[j]: # 升序
li[j+1], li[j] = li[j], li[j+1]
exchange = True
# 如果标志位没有变化,则说明这一趟中数字位置没有发生变化(即已经有序了),后面的趟没必要比较了
if not exchange:
return
li = [1, 2, 5, 3, 4, 6, 9, 8, 7]
bubble_sort(li)
print(li)
小结:
- 选择排序时间复杂度:O的二次方
- 原地排序
- 比较时都是相邻的数进行比较(埃个比较),具有稳定性
2、选择排序(Selection Sort)
算法描述
每一趟选择一个数放在第一位,然后后面每个数都与这个数进行比较,如果比第一位数小的话就替换掉第一个数,然后后面的数再和新的最小值比较,一趟完成过后有序区产生一个有序数字,然后每一趟都循环无序区中的数字。
动图演示

代码演示
def select_sort(nums):
# 因为遍历了n-1次之后 最后一个值肯定是最大的了,无序再遍历
for i in range(len(nums) - 1):
min_pos = i # 当前遍历目标位置
# i后面所有的数都和 目标位置的数值进行比较
for j in range(i + 1, len(nums)):
if nums[j] < nums[min_pos]:
min_pos = j
nums[min_pos], nums[i] = nums[i], nums[min_pos]
return nums
小结:
- 时间复杂度也是n方
- 原地排序
- 排序时发现一个数比第一个数小,直接隔离很多数换去第一个位置(跳着换),不具有稳定性。比如:[2,3,2,1,4], 1和第一个2换了,两个2的相对位置发生了变化
- 和冒泡排序的区别,稳定性和不稳定性,冒泡排序的无序区在每一趟后面,选择排序的无序区在每一趟前面。
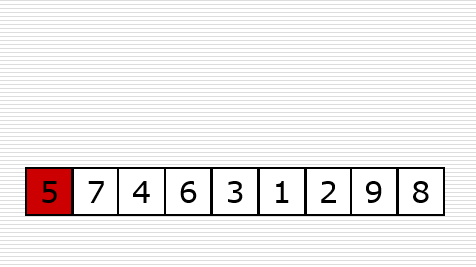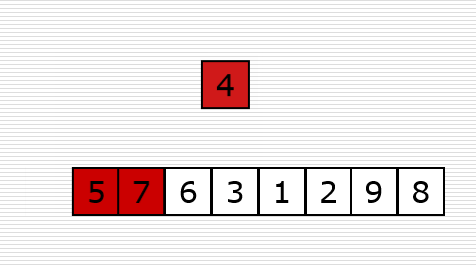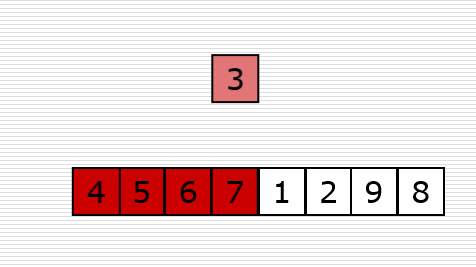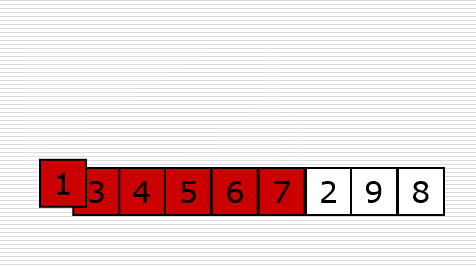
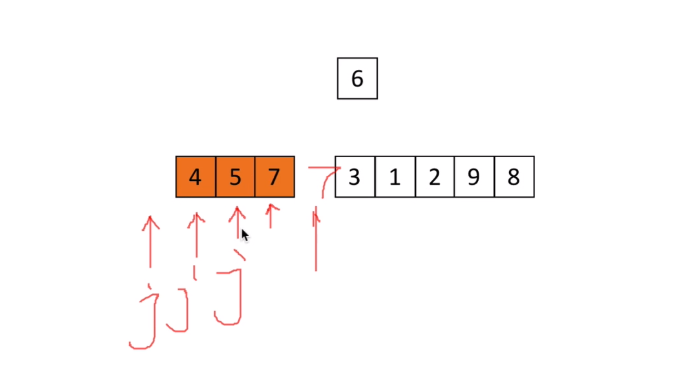
3、插入排序(Insertion Sort)
算法描述
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置插入。
实现思路:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列从后向前扫描
- 如果该元素大于新元素,则该元素移动到下一位置。
动图演示
代码实现
def insert_sort(nums):
for i in range(1, len(nums)):
temp = nums[i] # 要插入的值
j = i - 1 # j为有序区中最大的值
while j >= 0 and nums[j] > temp: # 有序区中 所有比temp大的值全部往右移动
nums[j + 1] = nums[j]
j -= 1
nums[j + 1] = temp
return nums
小结:
- 时间复杂度:n方
- 原地排序
- 没有跳着(跳着无序区的数字)插入,所以具有稳定性。



