堆排序
此次分享的堆排序实现代码是没有使用递归的,在开始之前,要先补给几个知识。
知识补给1:完全二叉树
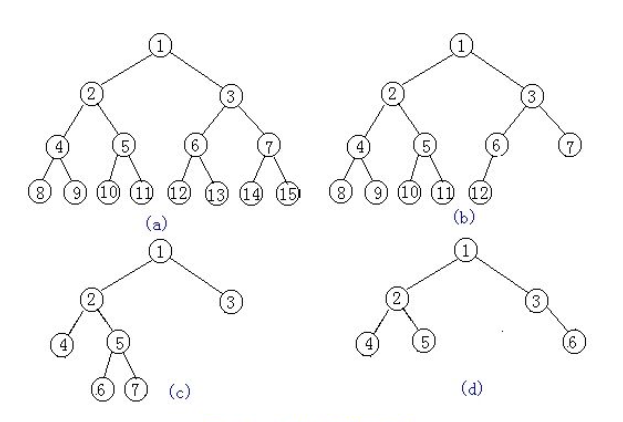
满二叉树:一个二叉树,如果每一层的节点数都达到最大值,则这个二叉树就是满二叉树。
在上图中,只有(a)是满二叉树。
完全二叉树:叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
(也就是说,相对比满二叉树而言,他可以缺少子节点,但是只能从最后按顺序缺)
在上图中,b、c、d都缺少子节点,但b是在最底层而且从最右边开始缺,所以b是完全二叉树。
而我们的推排序是一种特殊的完全二叉树!!!!!
知识补给2:二叉树的顺序储存方式
二叉树的存储方式(表示方式)有两种
- 链式存储方式
- 顺序存储方式(列表)
而堆排序用的是二叉树的顺序存储方式。
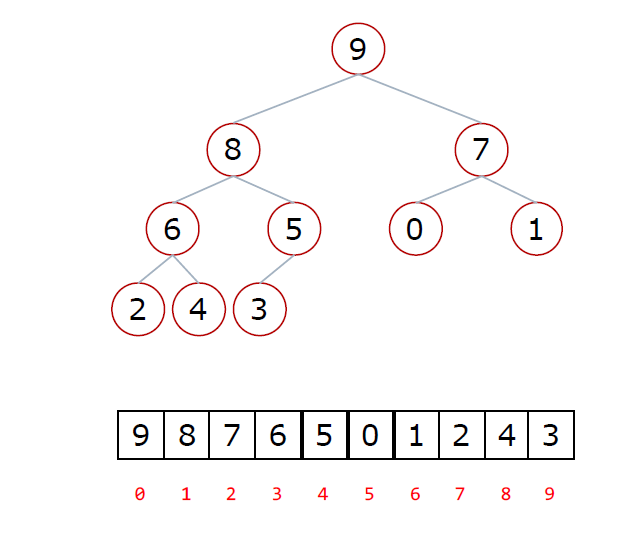
我们来看一下这颗完全二叉树里面存储的数据的下标规律:
它是根据列表从左到右的顺序存储到树里面的。这样我们就可以观察一下父节点和子节点的下标关系了
父节点和左孩子节点的关系(节点的值:下标)
9 - 8 : 0 - 1 8 - 6 : 1 - 3 6 - 2 : 3 - 7
用数学归纳法可以发现规律: i = 2i + 1
父节点和右孩子节点的关系(节点的值:下标)
9 - 7:0 - 2 8 - 5:1 - 4 7 - 1:2 - 6
用数学归纳法可以发现规律: i = 2i + 2
相同的,我们可以根据子节点的下标反推出父节点的下表:(i - 1) // 2
知识补给3:什么是堆
堆:一种特殊的完全二叉树结构
大根堆:一颗完全二叉树,满足任一节点都比其孩子节点大
小根堆:一颗完全二叉树,满足任一节点都比其孩子节点小

知识补给4:堆的向下调整性质
- 假设根节点的左右子树都是堆,但根节点不满足堆的性质(大根堆,小根堆)
- 可以通过一次向下的调整来将其变成一个堆
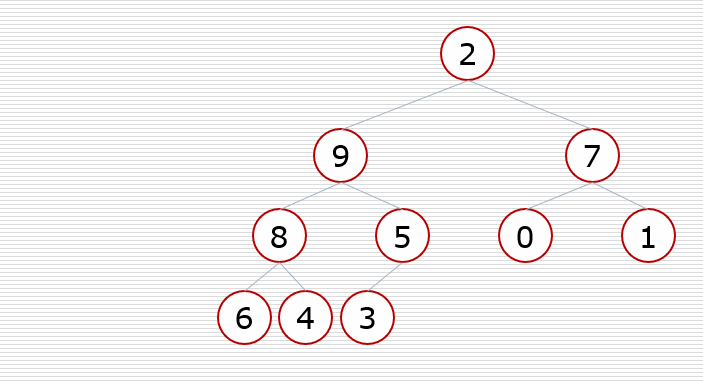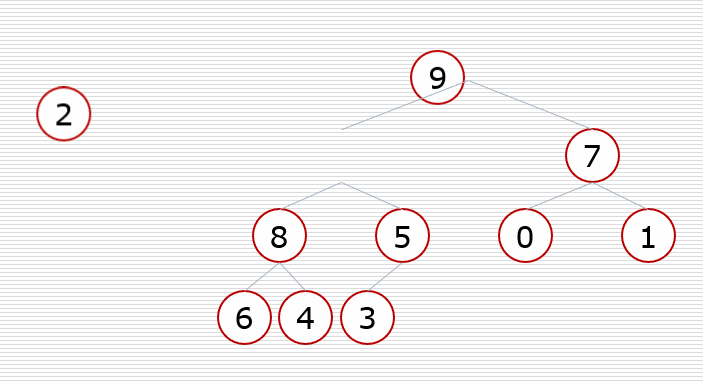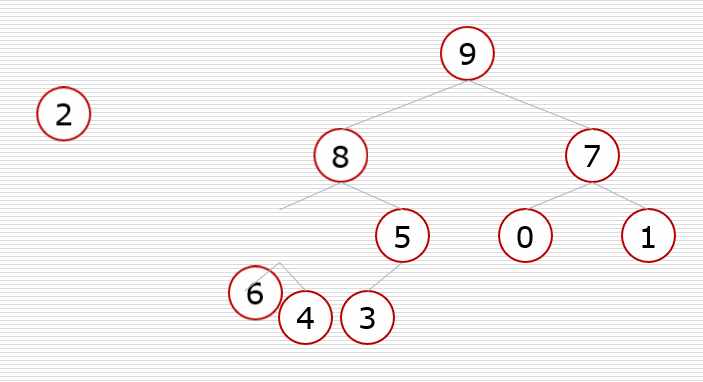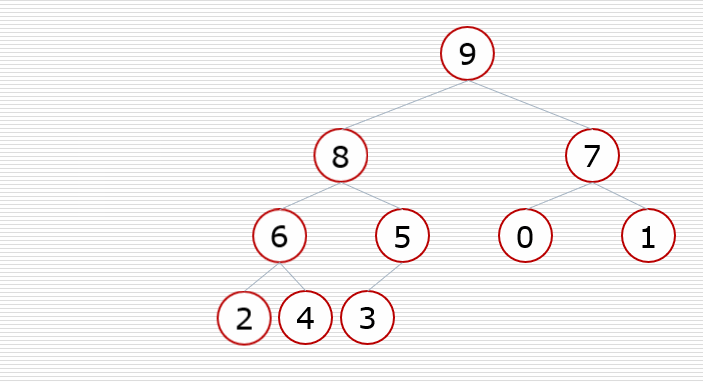
堆排序过程:
- 建立堆
- 得到堆顶元素,为最大元素
- 去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。
- 堆顶元素为第二大元素
- 重复步骤3,直到堆变空
构造堆(农村包围城市)
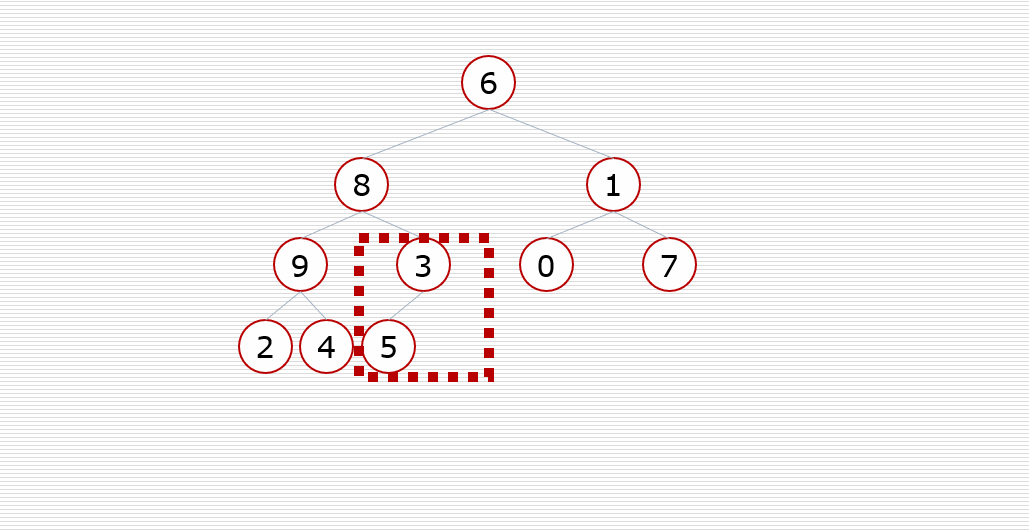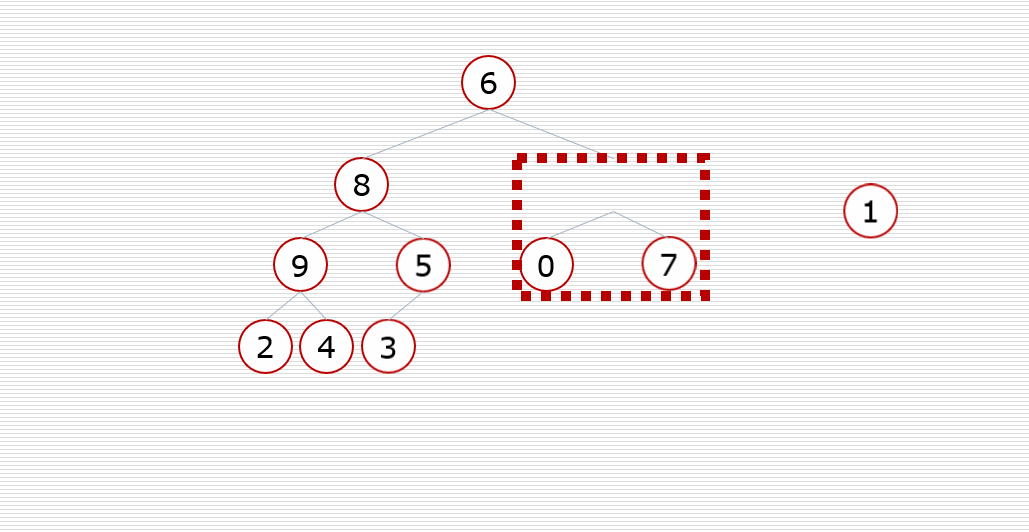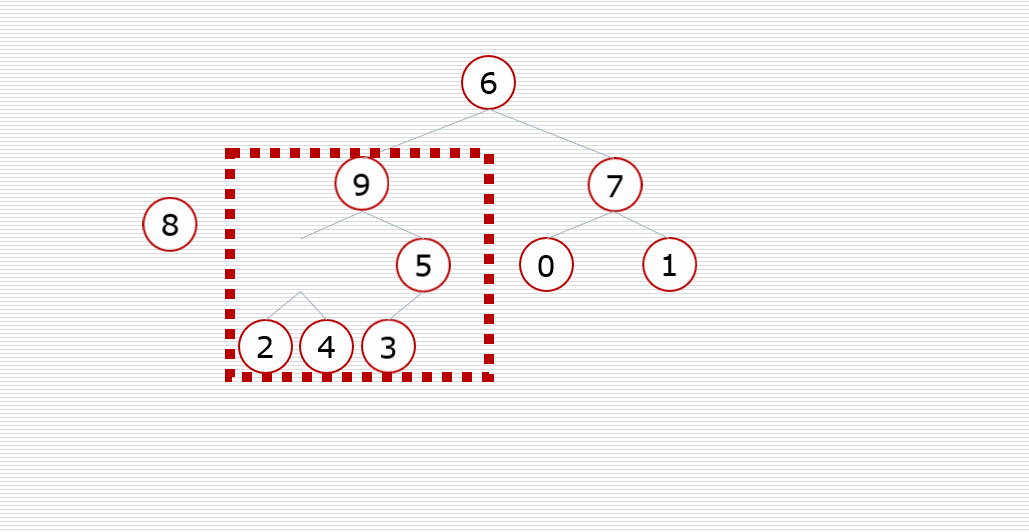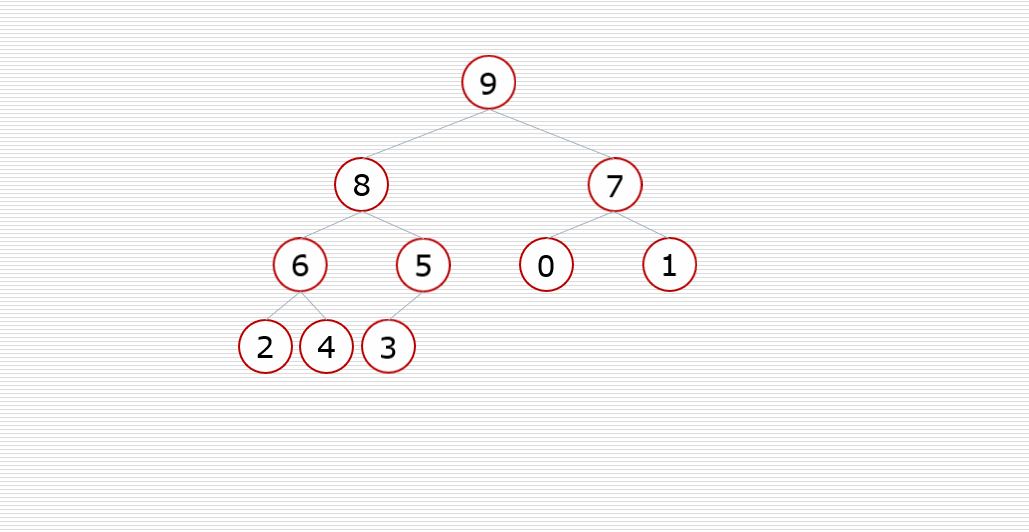
堆排序的实现过程中,其实大部分过程都在调整过程(建立堆,排序的时候去掉堆顶,重新调整)
所以我们先来实现调整堆的代码
def sift(li, low, high):
"""
调整堆的顺序,使其称为大根堆or小根堆
:param li: 要排序的列表
:param low: 堆的根节点的位置
:param high: 堆最后一个元素的位置(边界)
:return:
"""
# 首先要定义两个变量来记录父节点和子节点的位置
i = low # 父节点
j = 2 * i + 1 # 左孩子节点
tmp = li[low] # 根节点的值
while j <= high: # 只要不超过边界就一直与子节点比较大小进行调整
if j + 1 <= high and li[j + 1] > li[j]: # 如果右边节点存在且值比左边大,就把j指向右边的值的下标
j = j + 1
if li[j] > tmp: # 如果子节点的值大于父节点,就互相替换,然后进入下一层
li[i] = li[j]
i = j
j = 2 * i + 1
else:
# tmp的值比子节点的值大,直接跳出循环,下面的子树也不用比较了,因为下面的树是已经有序了的,例如(第一层无序,调整完位置之后,tmp都比第二层的子节点大,此时第二层的父节点是i,就把tmp赋值给i)
# 因为构建堆的时候是农村包围城市的,即从最靠后面的子树开始建堆的
li[i] = tmp
break
else:
# 超出了边界,直接替换子节点
li[i] = tmp
写完这个调整位置的函数之后,我们实现堆排序的代码就很简单了。
def heap_sort(li): """ 实现堆排序过程: 1、先根据传入的列表构建堆(大根堆) 2、再埃个出数 :param li: :return: """ n = len(li) # 1、构建堆--农村包围城市 for i in range((n-2)//2, -1, -1): # i 就是每个父节点的位置 # (n-2)//2 是根据堆的最后一个叶子节点位置推算其父节点位置的公式:(i-1)//2 # 而 i 又等于 n - 1, 所以 (i-1)//2 == ((n - 1)-1)//2 == (n-2)//2 # 第一个 -1 ,因为要从最后一个根节点循环到第一个根节点也就是列表中下标为0的元素,range 为开头闭尾 # 第二个 -1, 倒序 sift(li, i, n-1) # 2、埃个出数,完成列表排序, # 原地排序,每次都根节点都和最后一个叶子节点互换,然后调整位置, 再进行如上循环操作,直到堆为空 for i in range(n-1, -1, -1): # i是每次循环堆里面最后一个数 li[0], li[i] = li[i], li[0] sift(li, 0, i-1) # 边界值下标, 因为出数完之后,最后原i位置上的元素是出数的结果,所以i位置上的元素不参加调整,故边界值为i-1.
到此,堆排序的代码就实现完成了,我们可以来简单测试一下。
li = [i for i in range(100)] import random random.shuffle(li) print(li) heap_sort(li) print(li) [26, 16, 81, 29, 11, 75, 73, 0, 35, 21, 95, 37, 72, 79, 80, 46, 76, 1, 93, 45, 25, 48, 92, 77, 42, 40, 82, 10, 6, 67, 30, 96, 47, 51, 38, 60, 4, 61, 64, 97, 33, 71, 8, 59, 87, 49, 19, 22, 83, 44, 9, 28, 27, 99, 69, 12, 2, 34, 24, 85, 32, 53, 14, 88, 90, 41, 55, 39, 20, 94, 63, 23, 7, 66, 84, 74, 62, 58, 56, 70, 86, 17, 89, 13, 18, 65, 50, 98, 5, 54, 15, 78, 3, 57, 31, 52, 68, 43, 36, 91] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99]
堆排序-- topk问题
现在有n个数,设计算法得到前k大的数。 (k<n)
解决思路:
- 排序后切片 O(nlogn) 切片时间忽略不计
- 排序lowb三人组 O(kn)
- 堆排序思路 O(nlogk) n个数进来堆比较logk次,
# 实现思路 # 1、创建一个小根堆 # 2、循环列表里面的数,和小根堆的根值比较,如果比根值要大,则替换小根堆的根值,然后再调整一次根堆 # 3、出数 def sift(li, low, high): """ 调整位置 :param li: :param low: 根堆的小的值的位置 :param high: 根堆的边界值 :return: """ i = low tmp = li[low] j = 2 * i + 1 # 左边孩子的下标 while j <= high: # 只要不超过边界值 父节点和子节点就会继续相比较 if j + 1 <= high and li[j + 1] < li[j]: # 如果j+1没有超过边界值,且比j对应的值小, j则指向j+1 j = j + 1 if li[j] < tmp: li[i] = li[j] i = j # 进入下一层 j = 2 * i + 1 else: li[i] = tmp break else: li[i] = tmp def topk(li, num): head = li[0: num] # 1、构建小根堆 (i-1)//2 for i in range((num - 2) // 2, -1, -1): # i 表示每一根节点的位置 sift(head, i, num-1) # 2、循环列表每一个数与小根堆的根值进行比较 for i in range(num, len(li)): if li[i] > head[0]: head[0] = li[i] sift(head, 0, num-1) # 3、出数 for i in range(num-1, -1, -1): # i 表示最后一个数的位置 head[0], head[i] = head[i], head[0] sift(head, 0, i-1) return head li = [i for i in range(1000)] import random random.shuffle(li) print(topk(li, 100))



